2020-2021学年人教版数学八年级下册17.1《勾股定理》同步测试(word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册17.1《勾股定理》同步测试(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 22:32:20 | ||
图片预览

文档简介
2021年人教版数学八年级下册《勾股定理》
同步测试
一、选择题
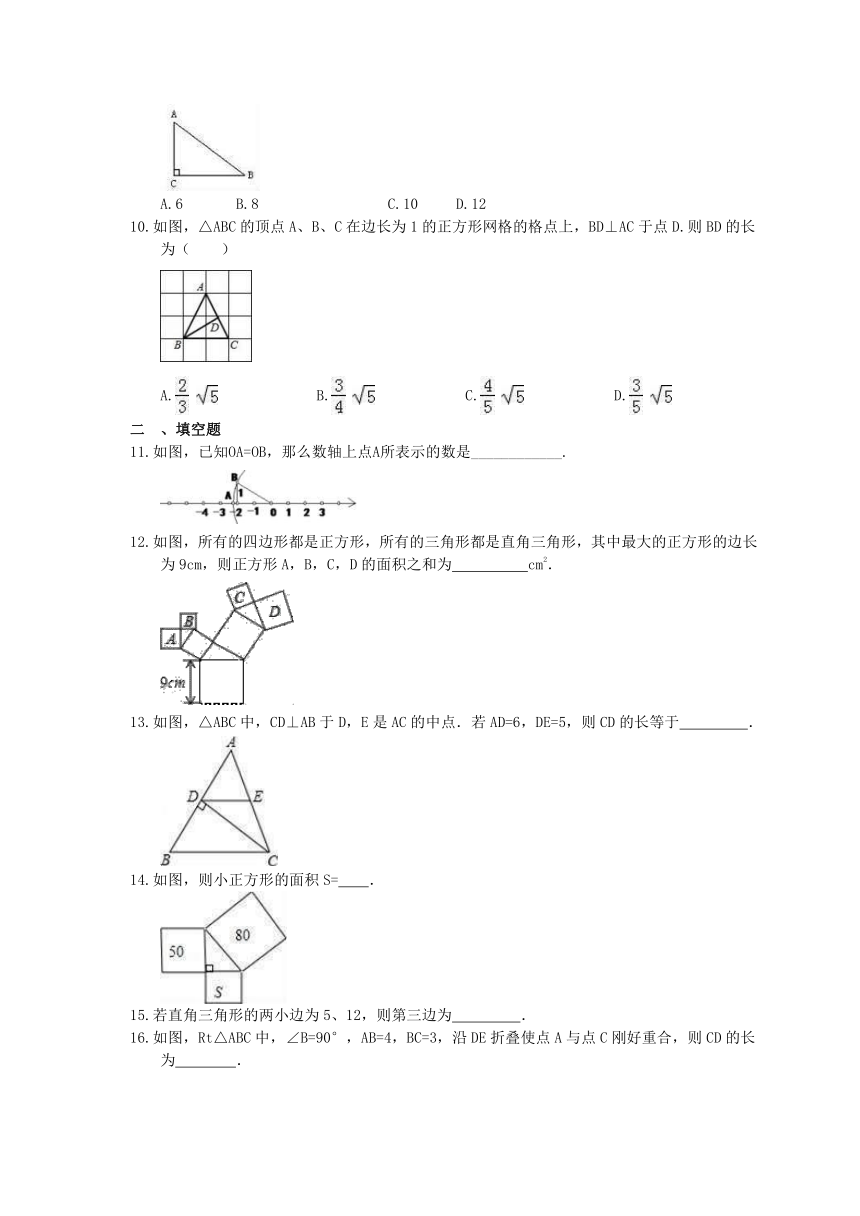
1.下列长度的各组线段,能组成直角三角形的是( )
A.12,15,18?? B.12,35,36?? C.0.3,0.4,0.5?? D.2,3,4
2.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( )
A.6 B.9 C.12 D.18
3.在一个直角三角形中,若斜边的长是13,一条直角边的长为12,那么这个直角三角形的面积是( )
A.30 B.40 C.50 D.60
4.如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
A. B.﹣ C. D.﹣
5.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
6.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
7.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A.1??? ???? B.?? ? ???? C.??? ? ????? D.2
8.高为3,底边长为8的等腰三角形腰长为(?? ).
A.3?? ? B.4????? C.5??? D.6
9.如图,直角△ABC的周长为24,且AB:AC=5:3,则BC=(??? )
A.6??? B.8 ??? C.10?? D.12
10.如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD的长为( )
A. B. C. D.
二 、填空题
11.如图,已知OA=OB,那么数轴上点A所表示的数是____________.
12.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为 cm2.?
13.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
14.如图,则小正方形的面积S= .
15.若直角三角形的两小边为5、12,则第三边为 ?? .
16.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为 .
三、作图题
17.如图1和图2均是由边长为1的小正方形组成的网格,按要求用实线画出顶点在格点上的图形.
要求:
(1)在图形1中画出一个面积为2.5的等腰三角形ABC;
(2)在图2中画出一个直角三角形,使三边长均为不同的无理数.
四、解答题
18.如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
参考答案
1.答案为:C.
2.B
3.A
4.D
5.D
6.C
7.D
8.答案为:C
9.答案为:B
10.C.
11.答案为:;
12.答案为:81
13.答案是:8.
14.答案为:30.
15.答案为:13.
16.答案为:3.125.
17.解:(1)如图1所示,△ABC为所求三角形;
(2)如图2所示,直角三角形为所求三角形.
18.(1)证明:∵△ACB与△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,∴∠ACE=∠BCD=90°﹣∠ACD,
在△ACE和△BCD中∴△ACE≌△BCD;
(2)解:∵△ACE≌△BCD,∴AE=BD,∠EAC=∠B=45°,
∵BD=12,∴∠EAD=45°+45°=90°,AE=12,
在Rt△EAD中,∠EAD=90°,DE=13,AE=12,由勾股定理得:AD=5,
∴AB=BD+AD=12+5=17.
同步测试
一、选择题
1.下列长度的各组线段,能组成直角三角形的是( )
A.12,15,18?? B.12,35,36?? C.0.3,0.4,0.5?? D.2,3,4
2.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( )
A.6 B.9 C.12 D.18
3.在一个直角三角形中,若斜边的长是13,一条直角边的长为12,那么这个直角三角形的面积是( )
A.30 B.40 C.50 D.60
4.如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
A. B.﹣ C. D.﹣
5.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
6.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
7.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A.1??? ???? B.?? ? ???? C.??? ? ????? D.2
8.高为3,底边长为8的等腰三角形腰长为(?? ).
A.3?? ? B.4????? C.5??? D.6
9.如图,直角△ABC的周长为24,且AB:AC=5:3,则BC=(??? )
A.6??? B.8 ??? C.10?? D.12
10.如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD的长为( )
A. B. C. D.
二 、填空题
11.如图,已知OA=OB,那么数轴上点A所表示的数是____________.
12.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积之和为 cm2.?
13.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
14.如图,则小正方形的面积S= .
15.若直角三角形的两小边为5、12,则第三边为 ?? .
16.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为 .
三、作图题
17.如图1和图2均是由边长为1的小正方形组成的网格,按要求用实线画出顶点在格点上的图形.
要求:
(1)在图形1中画出一个面积为2.5的等腰三角形ABC;
(2)在图2中画出一个直角三角形,使三边长均为不同的无理数.
四、解答题
18.如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.
参考答案
1.答案为:C.
2.B
3.A
4.D
5.D
6.C
7.D
8.答案为:C
9.答案为:B
10.C.
11.答案为:;
12.答案为:81
13.答案是:8.
14.答案为:30.
15.答案为:13.
16.答案为:3.125.
17.解:(1)如图1所示,△ABC为所求三角形;
(2)如图2所示,直角三角形为所求三角形.
18.(1)证明:∵△ACB与△ECD都是等腰直角三角形,
∴CE=CD,AC=BC,∠ACB=∠ECD=90°,∠B=∠BAC=45°,∴∠ACE=∠BCD=90°﹣∠ACD,
在△ACE和△BCD中∴△ACE≌△BCD;
(2)解:∵△ACE≌△BCD,∴AE=BD,∠EAC=∠B=45°,
∵BD=12,∴∠EAD=45°+45°=90°,AE=12,
在Rt△EAD中,∠EAD=90°,DE=13,AE=12,由勾股定理得:AD=5,
∴AB=BD+AD=12+5=17.
