2020-2021学年人教版数学八年级下册18.2.3《正方形》随堂练习(word含答案)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.2.3《正方形》随堂练习(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 22:56:54 | ||
图片预览

文档简介
2021年人教版数学八年级下册《正方形》
随堂练习
一、选择题
1.已知正方形的边长为2cm,则其对角线长是( )
A.4cm B.8cm C.cm D.2cm
2.菱形、矩形、正方形都具有的性质是( )
A.对角线相等
B.对角线互相垂直
C.对角线互相平分
D.对角线平分一组对角
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
4.下列说法中,错误的是( )
A.一组对边平行且相等的四边形是平行四边形
B.两条对角线互相垂直且平分的四边形是菱形
C.四个角都相等的四边形是矩形
D.邻边相等的菱形是正方形
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
6.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
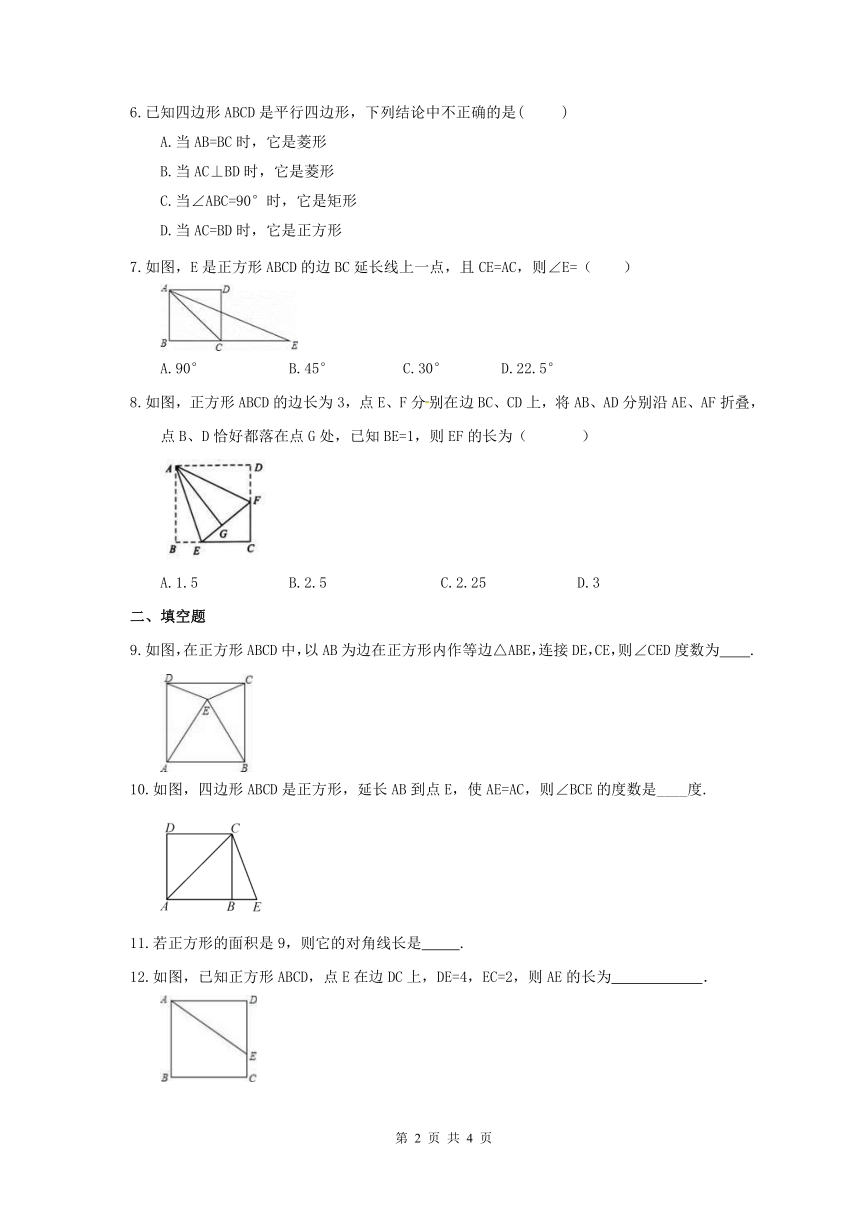
7.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A.90°????? B.45°???? C.30°??? D.22.5°
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为(??? )
A.1.5 B.2.5 C.2.25 D.3
二、填空题
9.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED度数为 .
10.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是____度.
11.若正方形的面积是9,则它的对角线长是 .
12.如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为 .
13.如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=4,BF=3,则EF的长为____________.
14.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为__________.
三、解答题
15.已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
(1)△ADE≌△BAF;
(2)AF=BF+EF.
16.如图,已知点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
参考答案
1.D
2.C
3.D
4.D
5.D;
6.D.
7.D
8.B
9.答案为:150°.
10.答案为:22.5;
11.答案为:3
12.答案为.
13.答案为:7
14.答案为:2;
15.解:(1)由正方形的性质可知:AD=AB,
∵∠BAF+∠ABF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
在△ADE与△BAF中,∴△ADE≌△BAF(AAS)
(2)由(1)可知:BF=AE,∴AF=AE+EF=BF+EF
16.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
随堂练习
一、选择题
1.已知正方形的边长为2cm,则其对角线长是( )
A.4cm B.8cm C.cm D.2cm
2.菱形、矩形、正方形都具有的性质是( )
A.对角线相等
B.对角线互相垂直
C.对角线互相平分
D.对角线平分一组对角
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
4.下列说法中,错误的是( )
A.一组对边平行且相等的四边形是平行四边形
B.两条对角线互相垂直且平分的四边形是菱形
C.四个角都相等的四边形是矩形
D.邻边相等的菱形是正方形
5.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
6.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
7.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A.90°????? B.45°???? C.30°??? D.22.5°
8.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为(??? )
A.1.5 B.2.5 C.2.25 D.3
二、填空题
9.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED度数为 .
10.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是____度.
11.若正方形的面积是9,则它的对角线长是 .
12.如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为 .
13.如图所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=4,BF=3,则EF的长为____________.
14.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为__________.
三、解答题
15.已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
(1)△ADE≌△BAF;
(2)AF=BF+EF.
16.如图,已知点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
参考答案
1.D
2.C
3.D
4.D
5.D;
6.D.
7.D
8.B
9.答案为:150°.
10.答案为:22.5;
11.答案为:3
12.答案为.
13.答案为:7
14.答案为:2;
15.解:(1)由正方形的性质可知:AD=AB,
∵∠BAF+∠ABF=∠BAF+∠DAE=90°,∴∠ABF=∠DAE,
在△ADE与△BAF中,∴△ADE≌△BAF(AAS)
(2)由(1)可知:BF=AE,∴AF=AE+EF=BF+EF
16.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
