2020--2021学年苏科版七年级下册 第7章 《平面图形的认识(二)》 单元易错题(四)(Word版 含解析)
文档属性
| 名称 | 2020--2021学年苏科版七年级下册 第7章 《平面图形的认识(二)》 单元易错题(四)(Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 163.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览


文档简介
2020--2021学年七年级下册
第7章
《平面图形的认识(二)》
单元高频易错必刷题(四)
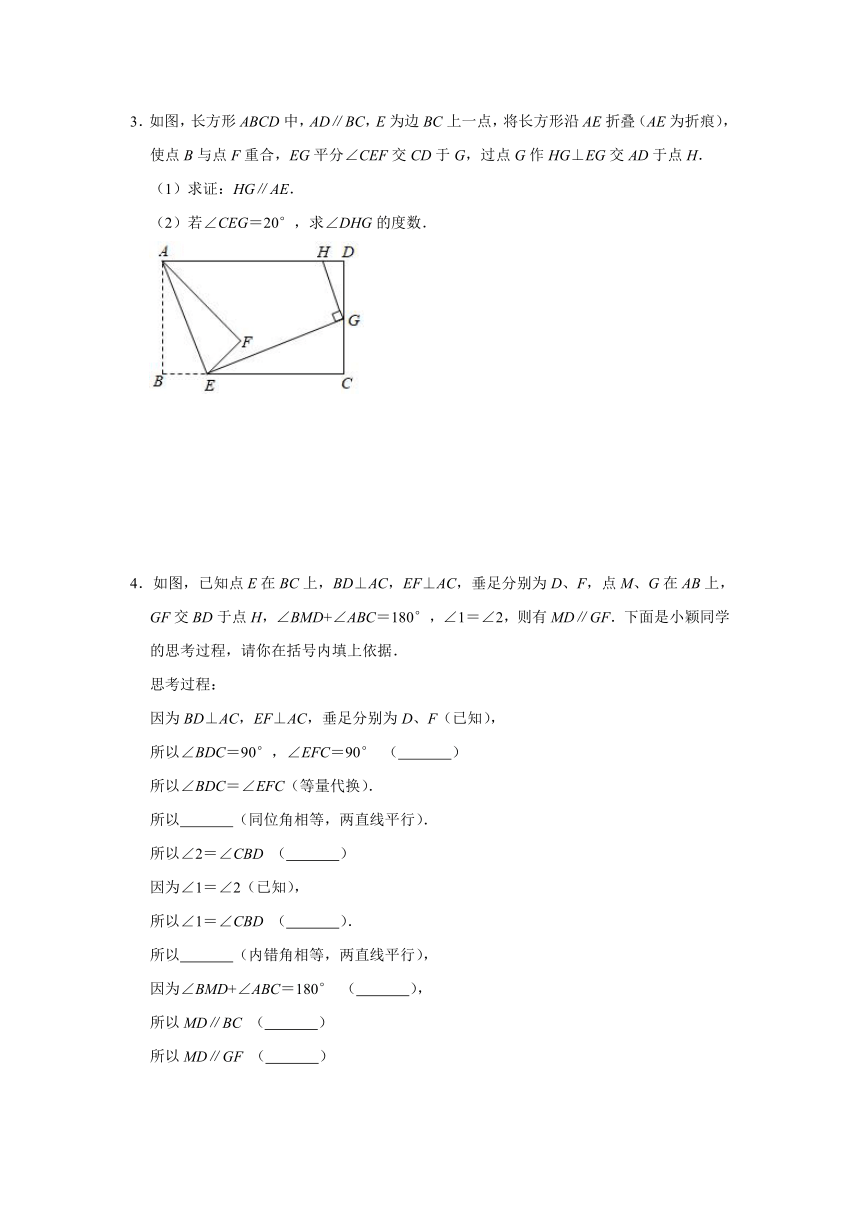
1.如图1,∠FBD=90°,EB=EF,CB=CD.
(1)求证:EF∥CD;
(2)如图2所示,若将△EBF沿射线BF平移,即EG∥BC,∠FBD=90°,EG=EF,CB=CD,请问(1)中的结论是否仍成立?请证明.
2.线段AB与线段CD互相平行,P是平面内的一点,且点P不在直线AB,CD上,连接PA,PD,射线AM,DN分别是∠BAP和∠CDP的平分线.
(1)若点P在线段AD上,如图1,
①依题意补全图1;
②判断AM与DN的位置关系,并证明;
(2)是否存在点P,使AM⊥DN?若存在,直接写出点P的位置;若不存在,说明理由.
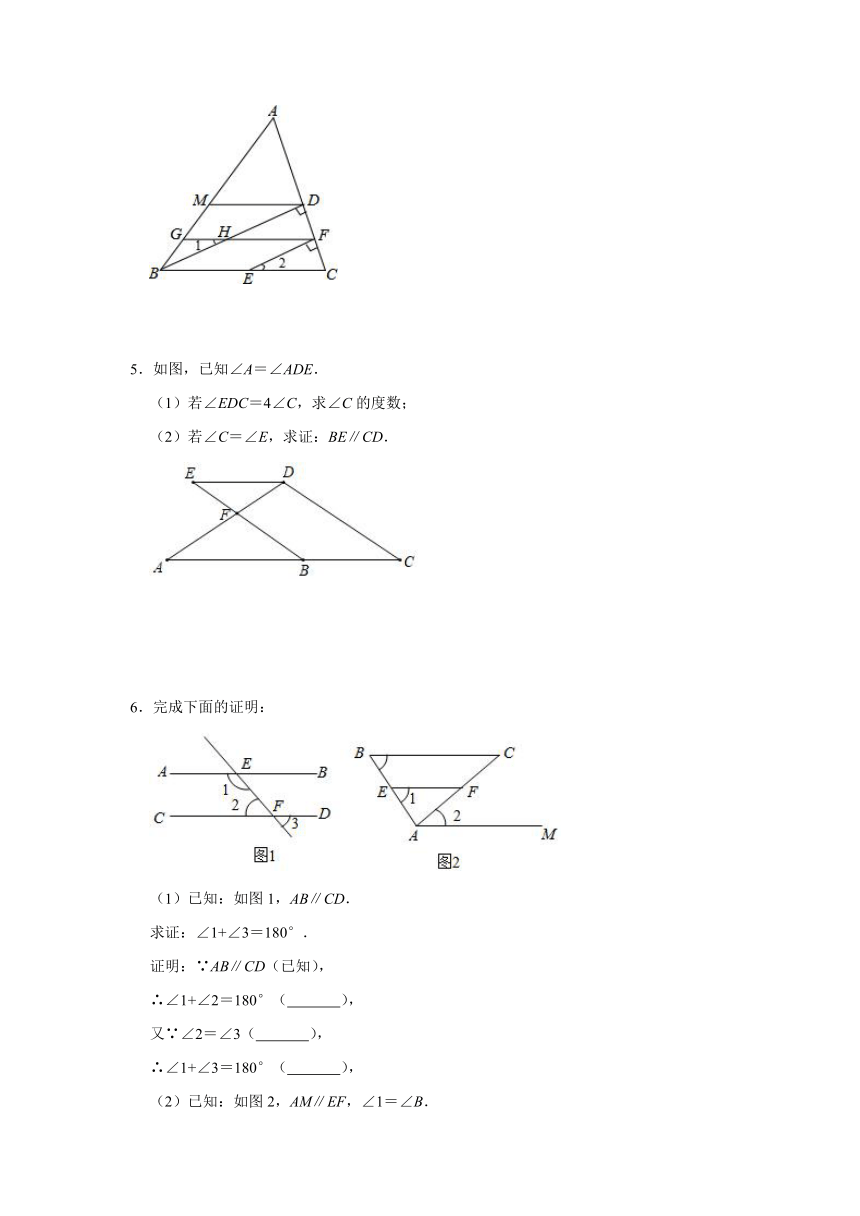
3.如图,长方形ABCD中,AD∥BC,E为边BC上一点,将长方形沿AE折叠(AE为折痕),使点B与点F重合,EG平分∠CEF交CD于G,过点G作HG⊥EG交AD于点H.
(1)求证:HG∥AE.
(2)若∠CEG=20°,求∠DHG的度数.
4.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,则有MD∥GF.下面是小颖同学的思考过程,请你在括号内填上依据.
思考过程:
因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°
(
)
所以∠BDC=∠EFC(等量代换).
所以
(同位角相等,两直线平行).
所以∠2=∠CBD
(
)
因为∠1=∠2(已知),
所以∠1=∠CBD
(
).
所以
(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°
(
),
所以MD∥BC
(
)
所以MD∥GF
(
)
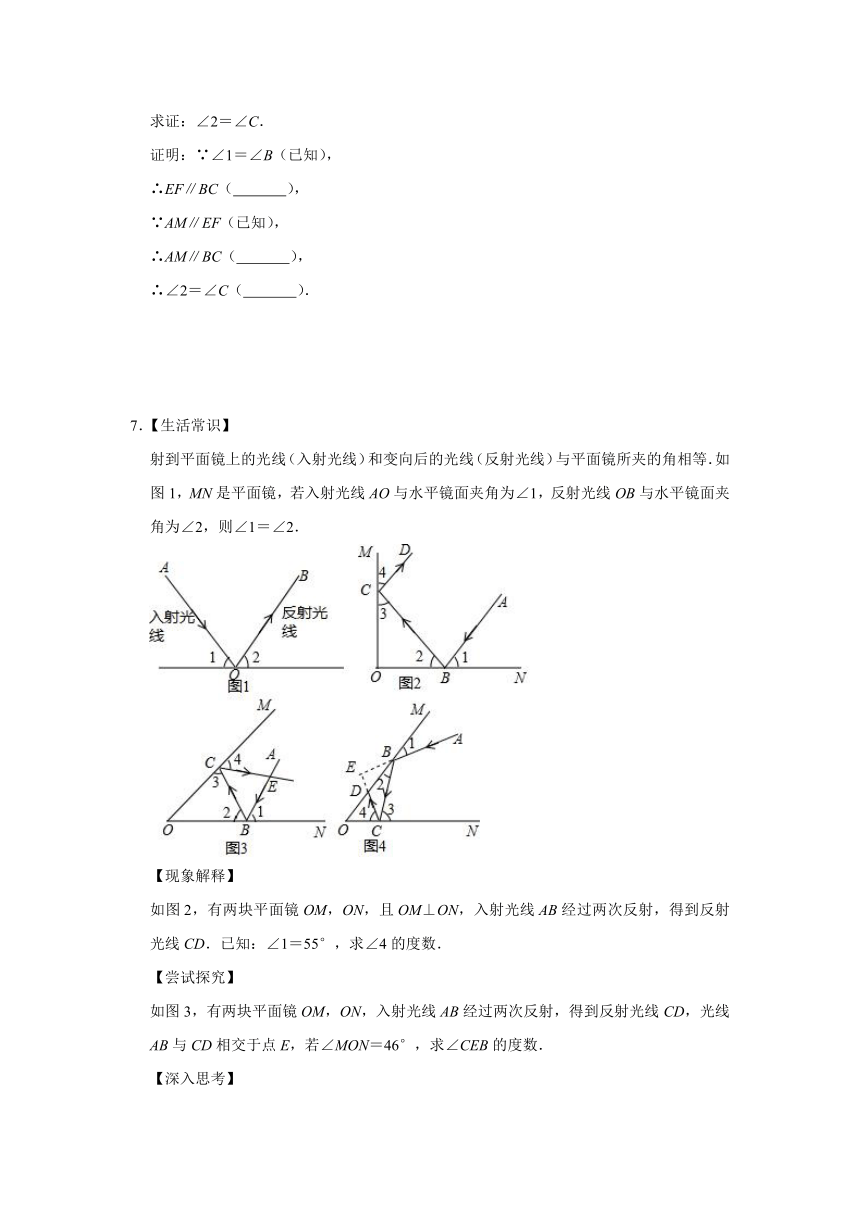
5.如图,已知∠A=∠ADE.
(1)若∠EDC=4∠C,求∠C的度数;
(2)若∠C=∠E,求证:BE∥CD.
6.完成下面的证明:
(1)已知:如图1,AB∥CD.
求证:∠1+∠3=180°.
证明:∵AB∥CD(已知),
∴∠1+∠2=180°(
),
又∵∠2=∠3(
),
∴∠1+∠3=180°(
),
(2)已知:如图2,AM∥EF,∠1=∠B.
求证:∠2=∠C.
证明:∵∠1=∠B(已知),
∴EF∥BC(
),
∵AM∥EF(已知),
∴AM∥BC(
),
∴∠2=∠C(
).
7.【生活常识】
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,MN是平面镜,若入射光线AO与水平镜面夹角为∠1,反射光线OB与水平镜面夹角为∠2,则∠1=∠2.
【现象解释】
如图2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.已知:∠1=55°,求∠4的度数.
【尝试探究】
如图3,有两块平面镜OM,ON,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD相交于点E,若∠MON=46°,求∠CEB的度数.
【深入思考】
如图4,有两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD所在的直线相交于点E,∠BED=β,α与β之间满足的等量关系是
.(直接写出结果)
8.完成推理填空:
已知,如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.试说明AD平分∠BAC.
证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠
=90°(垂直的定义),
∴AD∥EG(
),
∴∠1=∠2(
),
∠
=∠3,(两直线平行,同位角相等)
又∵∠E=∠1(已知),
∴∠
=∠
(等量代换),
∴AD平分∠BAC.
9.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.
小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”.即
已知:如图1,AB∥CD,E为AB、CD之间一点,连接AE,CE得到∠AEC.
求证:∠AEC=∠A+∠C.
小明笔记上写出的证明过程如下:
证明:过点E作EF∥AB,
∴∠1=∠A.
∵AB∥CD,EF∥AB,
∴EF∥CD.
∴∠2=∠C.
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C.
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
(1)如图2,若AB∥CD,∠E=60°,则∠B+∠C+∠F=
.
(2)如图3,AB∥CD,BE平分∠ABG,CF平分∠DCG,∠G=∠H+27°,E、B、H共线,F、C、H共线,则∠H=
.
10.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=
°.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
参考答案
1.(1)证明:如图1,连接FD,
∵EB=EF,CB=CD,
∴∠EBF=∠EFB,∠CBD=∠CDB,
∵∠FBD=90°,
∴∠EBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD;
(2)成立,
证明:如图2,连接FD,延长CB到H,
∵EG∥BC,
∴∠EGF=∠HBF,
∵∠FBD=90°,
∴∠HBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EGF+∠CBD=90°,
∵EG=EF,CB=CD,
∴∠EGF=∠EFB,∠CBD=∠CDB,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD.
2.解:(1)①根据题意作出图形如下:
②AM∥DN.
证明:∵AM平分∠BAD,DN平分∠CDA,
∴∠DAM=,,
∵AB∥CD,
∴∠BAD=∠CDA,
∴∠DAM=∠ADN,
∴AM∥DN;
(2)当P点在AD直线上,位于AB与CD两平行线之外时,AM⊥DN.
证明:如下图,
∵AB∥CD,
∴∠PAF=∠PDC,
∵∠PAF+∠PAB=180°,
∴∠PDC+∠PAB=180°,
∵AM平分∠BAP,DN平分∠CDA,
∴∠BAM=,,
∴∠CDN+∠BAM=90°,
∵AB∥CD,
∴∠AFD=∠CDN,
∵∠EAF=∠BAM,
∴∠AFE+∠EAF=90°,
∴∠AEF=90°,
∴AM⊥DN.
3.(1)证明:由折叠知∠AEB=∠AEF,
∵EG平分∠CEF,
∴∠FEG=∠CEG,
∵∠AEB+∠AEF+∠FEG+∠CEG=180°,
∴∠AEG=∠AEF+∠FEG=90°,
∴AE⊥EG,
∵HG⊥EG,
∴HG∥AE;
(2)解:∵∠CEG=20°,∠AEG=90°,
∴∠AEB=70°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠AEB=∠DAE=70°,
∵HG∥AE,
∴∠DHG=∠DAE=70°.
4.解:因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°(垂直的定义),
所以∠BDC=∠EFC(等量代换),
所以BD∥EF(同位角相等,两直线平行),
所以∠2=∠CBD(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠1=∠CBD(等量代换),
所以BC∥GF(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°(已知),
所以MD∥GF(同旁内角互补,两直线平行),
所以DM∥BC(平行于同一条直线的两条直线平行);
故答案为:垂直的定义;BD∥EF;两直线平行,同位角相等;等量代换;BC∥GF;已知;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
5.(1)解:∵∠A=∠ADE,
∴DE∥AC,
∴∠EDC+∠C=180°,
∵∠EDC=4∠C,
∴4∠C+∠C=180°,
解得,∠C=36°;
(2)证明:∵DE∥AC,
∴∠E=∠ABE,
∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
6.(1)证明:∵AB∥CD(已知),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
又∵∠2=∠3(对顶角相等),
∴∠1+∠3=180°(等量代换),
(2)证明:∵∠1=∠B(已知),
∴EF∥BC(同位角相等,两直线平行),
∵AM∥EF(已知),
∴AM∥BC(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠2=∠C(两直线平行,内错角相等).
故答案为:两直线平行,同旁内角互补;对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,内错角相等.
7.(1)解:如图2中,
∵∠1=∠2,∠1=55°.
∴∠2=55°.
∵OM⊥ON.
∴∠3=90°﹣∠2=90°﹣55°=35°.
∵∠4=∠3.
∴∠4=35°.
(2)解:如图3中,
∵∠MON=46°,
∴∠2+∠3=180°﹣∠MON=180°﹣46°=134°,
∵∠1=∠2,∠3=∠4,
∴∠ECB+∠EBC=360°﹣2(∠2+∠3)=360°﹣134°×2=92°,
∴∠BEC=180°﹣∠ECB﹣∠EBC=180°﹣92°=88°.
(3)解:结论:β=2α.
理由:如图4中,
∵∠E+∠EBD=∠O+∠4,∠4=∠3=∠O+∠2,∠1=∠2=∠EBD,
∴β+∠1=α+α+∠1,
∴β=2α.
8.证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3(两直线平行,同位角相等),
又∵∠E=∠1(已知),
∴∠2=∠3(等量代换),
∴AD平分∠BAC.
故答案为:EGC;同位角相等,两直线平行;两直线平行,内错角相等;E;2;3.
9.解:(1)过点E、F分别作EM∥AB,FN∥AB,如图2所示:
∵EM∥AB,
∴∠1=∠B,
又∵FN∥AB,
∴FN∥EM,
∴∠2=∠3,
又∵AB∥CD,
∴FN∥CD,
∴∠4+∠C=180°,
又∵∠BEF=∠1+∠2,∠EFC=∠3+∠4,∠BEF=60°
∴∠B+∠EFC+∠C=∠1+∠3+∠4+∠C
=(∠1+∠2)+(∠4+∠C)
=60°+180°
=240°;
(2)过点G、H作EF∥AB,MN∥AB,如图3所示:
∵BE平分∠ABG,CF平分∠DCG,
∴∠ABG=2∠1,∠DCG=2∠4,
又∵EF∥AB,
∴2∠1+∠7=180°,
又∵AB∥CD,
∴EF∥CD,
∴2∠4+∠8=180°,
∴∠7+∠8=360°﹣2(∠1+∠4),
又∵∠7+∠8+∠BGC=180°,
∴2(∠1+∠4)=∠BGC+180°,
又∵MN∥AB,
∴∠1=∠5,
又∵AB∥CD,
∴MN∥CD,
∴∠4=∠6,
∴2(∠5+∠6)=∠BGC+180°,
又∵∠5+∠6+∠BHC=180°,
∴∠BGC+2∠BHC=180°,
又∠BGC=∠BHC+27°,
∴3∠BHC+27°=180°,
∴∠BHC=51°;
故答案为:240°,51°.
10.解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:
过点A、D作射线AF,
∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C;
(2)①如图(2),∵∠X=90°,
由(1)知:∠A+∠ABX+∠ACX=∠X=90°,
∵∠A=40°,
∴∠ABX+∠ACX=50°,
故答案为:50;
②如图(3),∵∠A=40°,∠DBE=130°,
∴∠ADE+∠AEB=130°﹣40°=90°,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC==45°,
∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.
第7章
《平面图形的认识(二)》
单元高频易错必刷题(四)
1.如图1,∠FBD=90°,EB=EF,CB=CD.
(1)求证:EF∥CD;
(2)如图2所示,若将△EBF沿射线BF平移,即EG∥BC,∠FBD=90°,EG=EF,CB=CD,请问(1)中的结论是否仍成立?请证明.
2.线段AB与线段CD互相平行,P是平面内的一点,且点P不在直线AB,CD上,连接PA,PD,射线AM,DN分别是∠BAP和∠CDP的平分线.
(1)若点P在线段AD上,如图1,
①依题意补全图1;
②判断AM与DN的位置关系,并证明;
(2)是否存在点P,使AM⊥DN?若存在,直接写出点P的位置;若不存在,说明理由.
3.如图,长方形ABCD中,AD∥BC,E为边BC上一点,将长方形沿AE折叠(AE为折痕),使点B与点F重合,EG平分∠CEF交CD于G,过点G作HG⊥EG交AD于点H.
(1)求证:HG∥AE.
(2)若∠CEG=20°,求∠DHG的度数.
4.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,则有MD∥GF.下面是小颖同学的思考过程,请你在括号内填上依据.
思考过程:
因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°
(
)
所以∠BDC=∠EFC(等量代换).
所以
(同位角相等,两直线平行).
所以∠2=∠CBD
(
)
因为∠1=∠2(已知),
所以∠1=∠CBD
(
).
所以
(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°
(
),
所以MD∥BC
(
)
所以MD∥GF
(
)
5.如图,已知∠A=∠ADE.
(1)若∠EDC=4∠C,求∠C的度数;
(2)若∠C=∠E,求证:BE∥CD.
6.完成下面的证明:
(1)已知:如图1,AB∥CD.
求证:∠1+∠3=180°.
证明:∵AB∥CD(已知),
∴∠1+∠2=180°(
),
又∵∠2=∠3(
),
∴∠1+∠3=180°(
),
(2)已知:如图2,AM∥EF,∠1=∠B.
求证:∠2=∠C.
证明:∵∠1=∠B(已知),
∴EF∥BC(
),
∵AM∥EF(已知),
∴AM∥BC(
),
∴∠2=∠C(
).
7.【生活常识】
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,MN是平面镜,若入射光线AO与水平镜面夹角为∠1,反射光线OB与水平镜面夹角为∠2,则∠1=∠2.
【现象解释】
如图2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.已知:∠1=55°,求∠4的度数.
【尝试探究】
如图3,有两块平面镜OM,ON,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD相交于点E,若∠MON=46°,求∠CEB的度数.
【深入思考】
如图4,有两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD所在的直线相交于点E,∠BED=β,α与β之间满足的等量关系是
.(直接写出结果)
8.完成推理填空:
已知,如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.试说明AD平分∠BAC.
证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠
=90°(垂直的定义),
∴AD∥EG(
),
∴∠1=∠2(
),
∠
=∠3,(两直线平行,同位角相等)
又∵∠E=∠1(已知),
∴∠
=∠
(等量代换),
∴AD平分∠BAC.
9.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.
小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”.即
已知:如图1,AB∥CD,E为AB、CD之间一点,连接AE,CE得到∠AEC.
求证:∠AEC=∠A+∠C.
小明笔记上写出的证明过程如下:
证明:过点E作EF∥AB,
∴∠1=∠A.
∵AB∥CD,EF∥AB,
∴EF∥CD.
∴∠2=∠C.
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠C.
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
(1)如图2,若AB∥CD,∠E=60°,则∠B+∠C+∠F=
.
(2)如图3,AB∥CD,BE平分∠ABG,CF平分∠DCG,∠G=∠H+27°,E、B、H共线,F、C、H共线,则∠H=
.
10.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=
°.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
参考答案
1.(1)证明:如图1,连接FD,
∵EB=EF,CB=CD,
∴∠EBF=∠EFB,∠CBD=∠CDB,
∵∠FBD=90°,
∴∠EBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD;
(2)成立,
证明:如图2,连接FD,延长CB到H,
∵EG∥BC,
∴∠EGF=∠HBF,
∵∠FBD=90°,
∴∠HBF+∠CBD=90°,∠BFD+∠BDF=90°,
∴∠EGF+∠CBD=90°,
∵EG=EF,CB=CD,
∴∠EGF=∠EFB,∠CBD=∠CDB,
∴∠EFB+∠CDB=90°,
∴∠EFD+∠CDF=180°,
∴EF∥CD.
2.解:(1)①根据题意作出图形如下:
②AM∥DN.
证明:∵AM平分∠BAD,DN平分∠CDA,
∴∠DAM=,,
∵AB∥CD,
∴∠BAD=∠CDA,
∴∠DAM=∠ADN,
∴AM∥DN;
(2)当P点在AD直线上,位于AB与CD两平行线之外时,AM⊥DN.
证明:如下图,
∵AB∥CD,
∴∠PAF=∠PDC,
∵∠PAF+∠PAB=180°,
∴∠PDC+∠PAB=180°,
∵AM平分∠BAP,DN平分∠CDA,
∴∠BAM=,,
∴∠CDN+∠BAM=90°,
∵AB∥CD,
∴∠AFD=∠CDN,
∵∠EAF=∠BAM,
∴∠AFE+∠EAF=90°,
∴∠AEF=90°,
∴AM⊥DN.
3.(1)证明:由折叠知∠AEB=∠AEF,
∵EG平分∠CEF,
∴∠FEG=∠CEG,
∵∠AEB+∠AEF+∠FEG+∠CEG=180°,
∴∠AEG=∠AEF+∠FEG=90°,
∴AE⊥EG,
∵HG⊥EG,
∴HG∥AE;
(2)解:∵∠CEG=20°,∠AEG=90°,
∴∠AEB=70°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠AEB=∠DAE=70°,
∵HG∥AE,
∴∠DHG=∠DAE=70°.
4.解:因为BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
所以∠BDC=90°,∠EFC=90°(垂直的定义),
所以∠BDC=∠EFC(等量代换),
所以BD∥EF(同位角相等,两直线平行),
所以∠2=∠CBD(两直线平行,同位角相等),
因为∠1=∠2(已知),
所以∠1=∠CBD(等量代换),
所以BC∥GF(内错角相等,两直线平行),
因为∠BMD+∠ABC=180°(已知),
所以MD∥GF(同旁内角互补,两直线平行),
所以DM∥BC(平行于同一条直线的两条直线平行);
故答案为:垂直的定义;BD∥EF;两直线平行,同位角相等;等量代换;BC∥GF;已知;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
5.(1)解:∵∠A=∠ADE,
∴DE∥AC,
∴∠EDC+∠C=180°,
∵∠EDC=4∠C,
∴4∠C+∠C=180°,
解得,∠C=36°;
(2)证明:∵DE∥AC,
∴∠E=∠ABE,
∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
6.(1)证明:∵AB∥CD(已知),
∴∠1+∠2=180°(两直线平行,同旁内角互补),
又∵∠2=∠3(对顶角相等),
∴∠1+∠3=180°(等量代换),
(2)证明:∵∠1=∠B(已知),
∴EF∥BC(同位角相等,两直线平行),
∵AM∥EF(已知),
∴AM∥BC(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠2=∠C(两直线平行,内错角相等).
故答案为:两直线平行,同旁内角互补;对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,内错角相等.
7.(1)解:如图2中,
∵∠1=∠2,∠1=55°.
∴∠2=55°.
∵OM⊥ON.
∴∠3=90°﹣∠2=90°﹣55°=35°.
∵∠4=∠3.
∴∠4=35°.
(2)解:如图3中,
∵∠MON=46°,
∴∠2+∠3=180°﹣∠MON=180°﹣46°=134°,
∵∠1=∠2,∠3=∠4,
∴∠ECB+∠EBC=360°﹣2(∠2+∠3)=360°﹣134°×2=92°,
∴∠BEC=180°﹣∠ECB﹣∠EBC=180°﹣92°=88°.
(3)解:结论:β=2α.
理由:如图4中,
∵∠E+∠EBD=∠O+∠4,∠4=∠3=∠O+∠2,∠1=∠2=∠EBD,
∴β+∠1=α+α+∠1,
∴β=2α.
8.证明:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3(两直线平行,同位角相等),
又∵∠E=∠1(已知),
∴∠2=∠3(等量代换),
∴AD平分∠BAC.
故答案为:EGC;同位角相等,两直线平行;两直线平行,内错角相等;E;2;3.
9.解:(1)过点E、F分别作EM∥AB,FN∥AB,如图2所示:
∵EM∥AB,
∴∠1=∠B,
又∵FN∥AB,
∴FN∥EM,
∴∠2=∠3,
又∵AB∥CD,
∴FN∥CD,
∴∠4+∠C=180°,
又∵∠BEF=∠1+∠2,∠EFC=∠3+∠4,∠BEF=60°
∴∠B+∠EFC+∠C=∠1+∠3+∠4+∠C
=(∠1+∠2)+(∠4+∠C)
=60°+180°
=240°;
(2)过点G、H作EF∥AB,MN∥AB,如图3所示:
∵BE平分∠ABG,CF平分∠DCG,
∴∠ABG=2∠1,∠DCG=2∠4,
又∵EF∥AB,
∴2∠1+∠7=180°,
又∵AB∥CD,
∴EF∥CD,
∴2∠4+∠8=180°,
∴∠7+∠8=360°﹣2(∠1+∠4),
又∵∠7+∠8+∠BGC=180°,
∴2(∠1+∠4)=∠BGC+180°,
又∵MN∥AB,
∴∠1=∠5,
又∵AB∥CD,
∴MN∥CD,
∴∠4=∠6,
∴2(∠5+∠6)=∠BGC+180°,
又∵∠5+∠6+∠BHC=180°,
∴∠BGC+2∠BHC=180°,
又∠BGC=∠BHC+27°,
∴3∠BHC+27°=180°,
∴∠BHC=51°;
故答案为:240°,51°.
10.解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:
过点A、D作射线AF,
∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C;
(2)①如图(2),∵∠X=90°,
由(1)知:∠A+∠ABX+∠ACX=∠X=90°,
∵∠A=40°,
∴∠ABX+∠ACX=50°,
故答案为:50;
②如图(3),∵∠A=40°,∠DBE=130°,
∴∠ADE+∠AEB=130°﹣40°=90°,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC==45°,
∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
