2020—2021学年苏科版数学七年级下册 7.2 探索平行线的性质 教学课件(共26张ppt)
文档属性
| 名称 | 2020—2021学年苏科版数学七年级下册 7.2 探索平行线的性质 教学课件(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 758.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览





文档简介
第7章 平面图形的认识(二)
7.2 探索平行线的性质
七年级数学下册苏科版
1
平行线的性质
2
平行线的性质与判定的综合
1
新知导入
想一想:
下图的线段平行吗?
2
课程讲授
平行线的性质
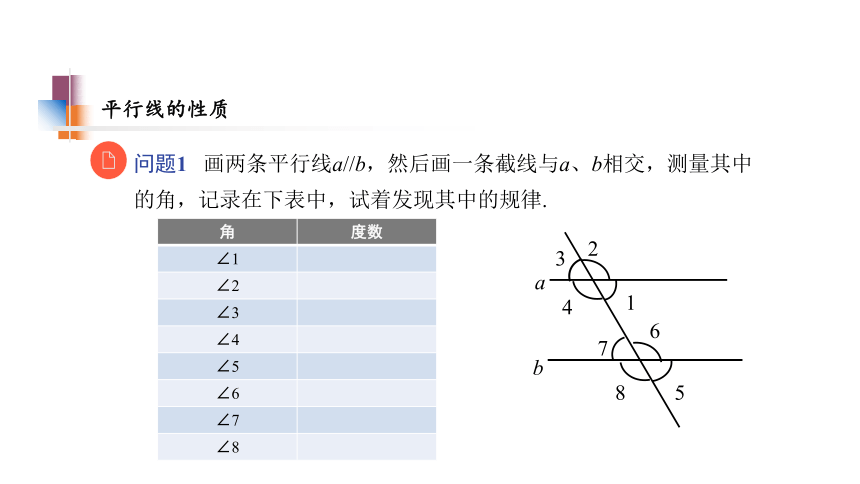
问题1 画两条平行线a//b,然后画一条截线与a、b相交,测量其中的角,记录在下表中,试着发现其中的规律.
b
a
2
1
3
4
6
5
8
7
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角
度数
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
平行线的性质
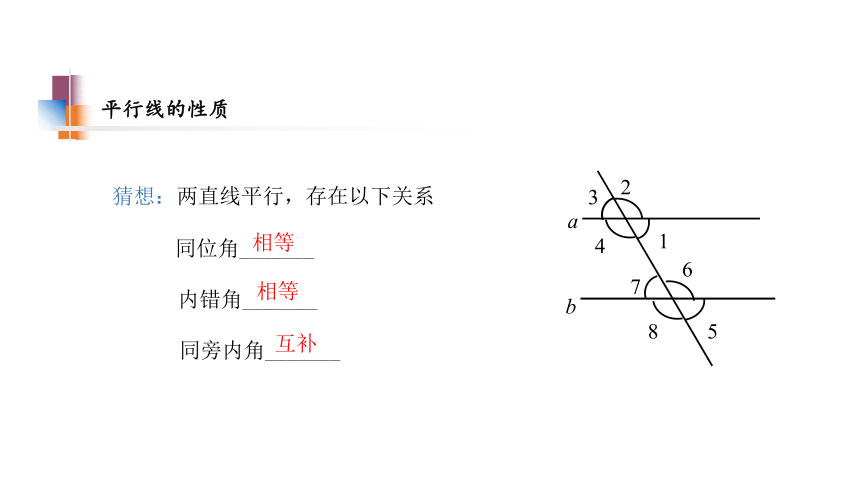
猜想:两直线平行,存在以下关系
同位角_______
同旁内角_______
内错角_______
相等
相等
互补
b
a
2
1
3
4
6
5
8
7
平行线的性质
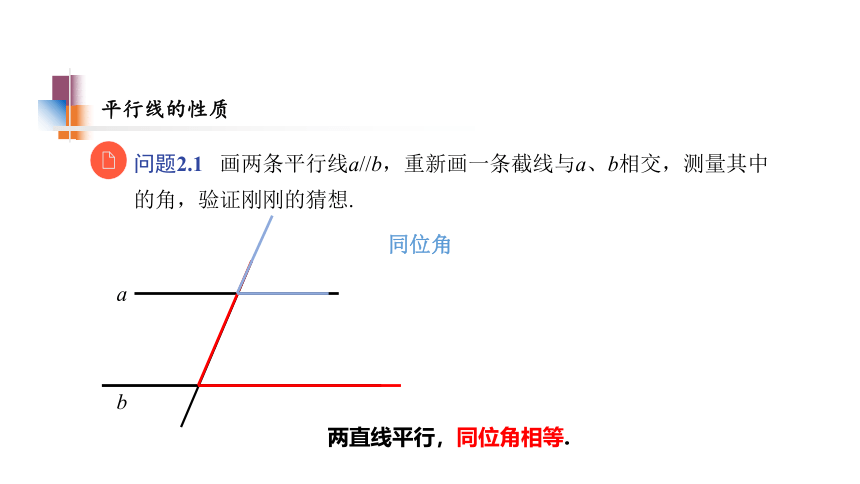
问题2.1 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
同位角
两直线平行,同位角相等.
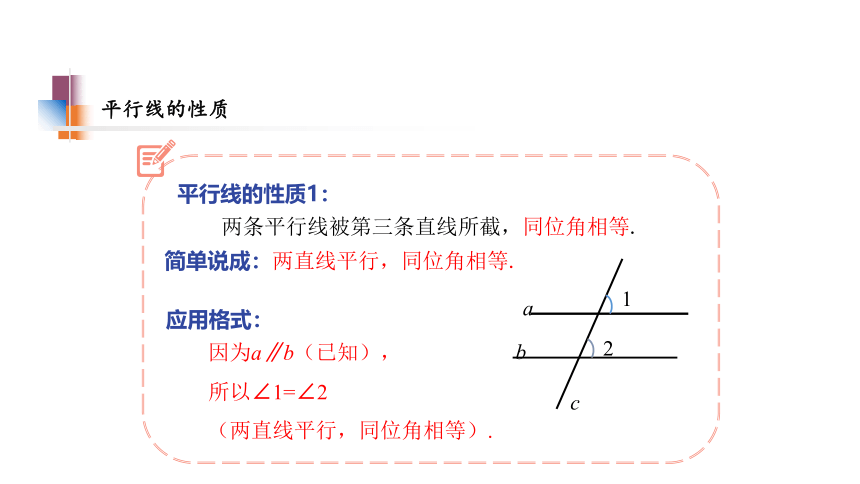
平行线的性质1:
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质
应用格式:
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等).
因为a∥b(已知),
平行线的性质
问题2.2 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
内错角
两直线平行,内错角相等.
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
平行线的性质
应用格式:
所以∠2=∠3
(两直线平行,内错角相等).
因为a∥b(已知),
b
1
2
a
c
3
平行线的性质
问题2.3 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
同旁内角
两直线平行,同旁内角互补.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
平行线的性质
应用格式:
所以∠2+∠3==180 °
(两直线平行,同旁内角互补).
因为a∥b(已知),
b
1
2
a
c
3
平行线的性质
练一练: 如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
∵AB∥CD,
∴∠2=∠BCE(两直线平行,内错角相等),
∵AD∥BC,
∴∠1=∠BCE(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
解:
平行线的性质与判定的综合
问题3 平行线的判定方法有哪三种?它们是先知道什么……后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的性质与判定的综合
问题4 平行线的“判定”与“性质”有什么不同?
已知角之间的关系(相等或互补),得到两直线平行的结论
是平行线的判定.
已知两直线平行,得到角之间的关系(相等或互补)的结论
是平行线的性质.
平行线的判定与平行线的性质的关系:
平行线的性质与判定的综合
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定的综合
例 如图,AB∥CD,∠A=∠D.判断AF与ED是否平行,并说明理由.
解:AF // ED.
因为AB // CD,
所以∠D= ∠BED.
理由是:两直线平行,内错角相等.
这样,由∠A=∠D、∠D=∠BED,
可得∠A=∠BED.
因为∠A= ∠BED,
所以AF // ED.
理由是:同位角相等,两直线平行.
解:∵ AD∥BC,
∴∠C=∠CDE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CDE,
∴AB∥CD(同位角相等,两直线平行).
练一练: 如图,已知AD∥BC,∠A=∠C.试说明AB∥CD.
平行线的性质与判定的综合
3
随堂练习
1.如果有两条直线被第三条直线所截,那么必定有( )
A.内错角相等 B.同位角相等
C.同旁内角互补 D.以上都不对
D
2.∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须 ( )
A.∠1= ∠2 B.∠1+∠2=90°
C.2(∠1+∠2)=360°
D.∠1是钝角,∠2是锐角
C
3.如图,若AB∥DE ,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解:∠A =∠D.理由:
因为 AB∥DE( ),
所以∠A=∠_____ ( ).
因为 AC∥DF( ),
所以∠D=∠_____ ( ).
所以∠A=∠D ( ).
P
F
C
E
B
A
D
已知
CPE
两直线平行,同位角相等
已知
CPE
两直线平行,同位角相等
等量代换
4.如图,若AB∥DE ,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180°. 理由:
因为 AB∥DE( )
所以∠A=∠_______
( )
因为AC∥DF( )
所以∠D+ _______=180° ( )
所以∠A+∠D=180°( )
F
C
E
B
A
D
P
已知
CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
4
课堂小结
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
7.2 探索平行线的性质
七年级数学下册苏科版
1
平行线的性质
2
平行线的性质与判定的综合
1
新知导入
想一想:
下图的线段平行吗?
2
课程讲授
平行线的性质
问题1 画两条平行线a//b,然后画一条截线与a、b相交,测量其中的角,记录在下表中,试着发现其中的规律.
b
a
2
1
3
4
6
5
8
7
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角
度数
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
平行线的性质
猜想:两直线平行,存在以下关系
同位角_______
同旁内角_______
内错角_______
相等
相等
互补
b
a
2
1
3
4
6
5
8
7
平行线的性质
问题2.1 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
同位角
两直线平行,同位角相等.
平行线的性质1:
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质
应用格式:
b
1
2
a
c
所以∠1=∠2
(两直线平行,同位角相等).
因为a∥b(已知),
平行线的性质
问题2.2 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
内错角
两直线平行,内错角相等.
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
平行线的性质
应用格式:
所以∠2=∠3
(两直线平行,内错角相等).
因为a∥b(已知),
b
1
2
a
c
3
平行线的性质
问题2.3 画两条平行线a//b,重新画一条截线与a、b相交,测量其中的角,验证刚刚的猜想.
b
a
同旁内角
两直线平行,同旁内角互补.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
平行线的性质
应用格式:
所以∠2+∠3==180 °
(两直线平行,同旁内角互补).
因为a∥b(已知),
b
1
2
a
c
3
平行线的性质
练一练: 如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
∵AB∥CD,
∴∠2=∠BCE(两直线平行,内错角相等),
∵AD∥BC,
∴∠1=∠BCE(两直线平行,同位角相等),
∴∠1=∠2(等量代换).
解:
平行线的性质与判定的综合
问题3 平行线的判定方法有哪三种?它们是先知道什么……后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的性质与判定的综合
问题4 平行线的“判定”与“性质”有什么不同?
已知角之间的关系(相等或互补),得到两直线平行的结论
是平行线的判定.
已知两直线平行,得到角之间的关系(相等或互补)的结论
是平行线的性质.
平行线的判定与平行线的性质的关系:
平行线的性质与判定的综合
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定的综合
例 如图,AB∥CD,∠A=∠D.判断AF与ED是否平行,并说明理由.
解:AF // ED.
因为AB // CD,
所以∠D= ∠BED.
理由是:两直线平行,内错角相等.
这样,由∠A=∠D、∠D=∠BED,
可得∠A=∠BED.
因为∠A= ∠BED,
所以AF // ED.
理由是:同位角相等,两直线平行.
解:∵ AD∥BC,
∴∠C=∠CDE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CDE,
∴AB∥CD(同位角相等,两直线平行).
练一练: 如图,已知AD∥BC,∠A=∠C.试说明AB∥CD.
平行线的性质与判定的综合
3
随堂练习
1.如果有两条直线被第三条直线所截,那么必定有( )
A.内错角相等 B.同位角相等
C.同旁内角互补 D.以上都不对
D
2.∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须 ( )
A.∠1= ∠2 B.∠1+∠2=90°
C.2(∠1+∠2)=360°
D.∠1是钝角,∠2是锐角
C
3.如图,若AB∥DE ,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解:∠A =∠D.理由:
因为 AB∥DE( ),
所以∠A=∠_____ ( ).
因为 AC∥DF( ),
所以∠D=∠_____ ( ).
所以∠A=∠D ( ).
P
F
C
E
B
A
D
已知
CPE
两直线平行,同位角相等
已知
CPE
两直线平行,同位角相等
等量代换
4.如图,若AB∥DE ,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180°. 理由:
因为 AB∥DE( )
所以∠A=∠_______
( )
因为AC∥DF( )
所以∠D+ _______=180° ( )
所以∠A+∠D=180°( )
F
C
E
B
A
D
P
已知
CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
4
课堂小结
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
