2020-2021学年九年级数学人教版下册 第二十七章 相似 培优综合练(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 第二十七章 相似 培优综合练(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 16:08:23 | ||
图片预览


文档简介
人教版九年级数学下册 第二十七章 相似
培优综合练
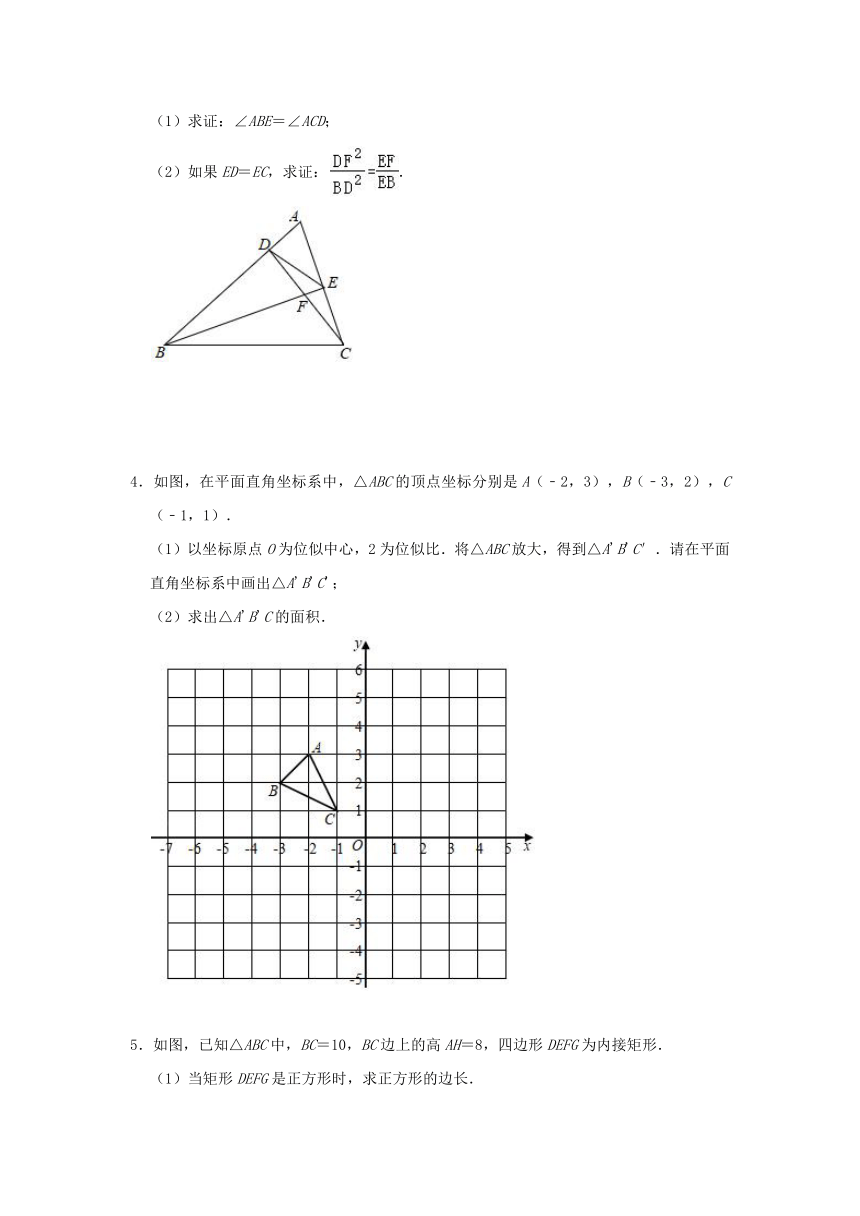
1.(1)拓展:如图①,在△ABC中,AB=AC,点D是AB上一点,点E是AC延长线上一点,且BD=CE.过点D作DF∥AC交BC于点F,连接DE交BC于点M.求证:BD=FD,FM=CM.
(2)应用:如图②,在上述“拓展”的条件下,另外增加条件∠A=90°,然后过点D作DN⊥BC,垂足为点N.若AC=1,则MN的长为 .
2.已知:如图,四边形ABCD是菱形,点M、N分别在边BC、CD上,联结AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.
(1)求证:AB2=BF?DE;
(2)若,求证:EF∥MN.
3.已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED=∠ABC,联结BE、CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:.
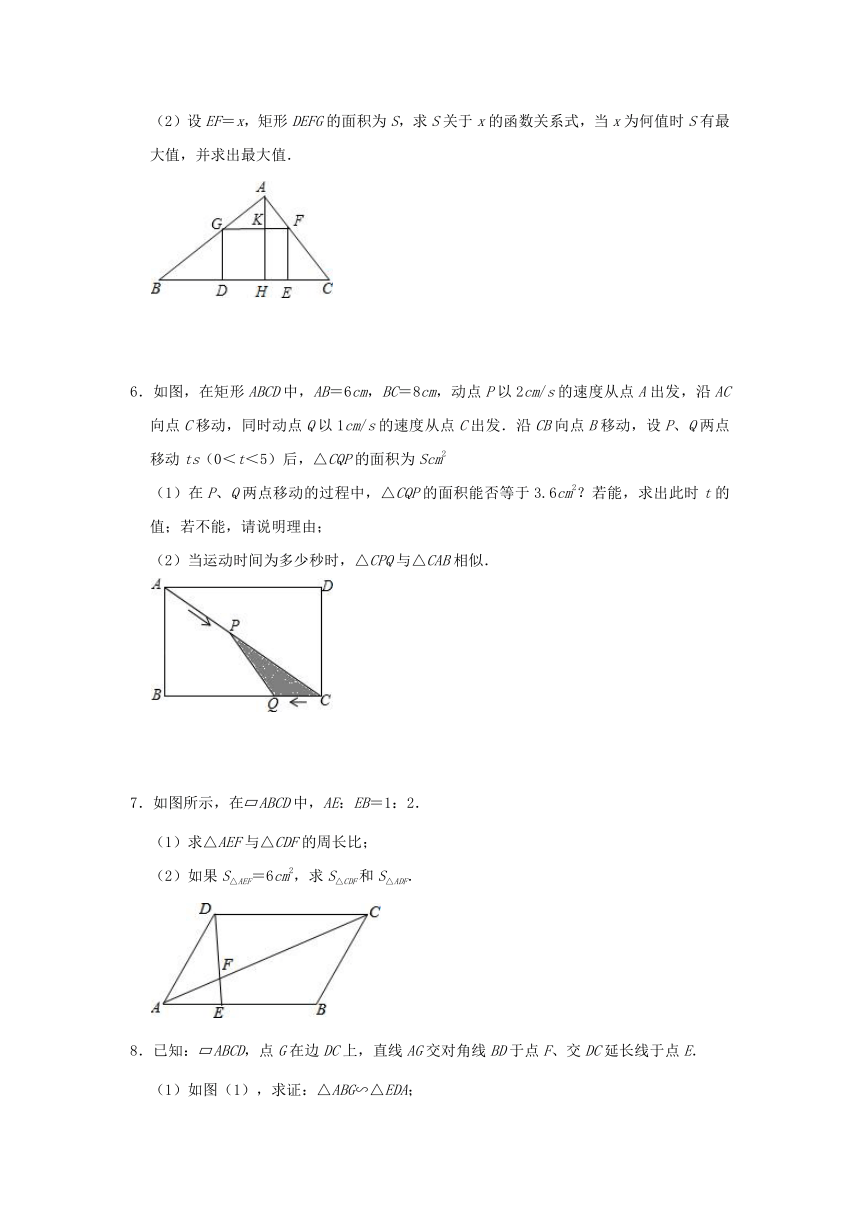
4.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A'B'C′.请在平面直角坐标系中画出△A'B'C';
(2)求出△A'B'C的面积.
5.如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
(1)当矩形DEFG是正方形时,求正方形的边长.
(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.
6.如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
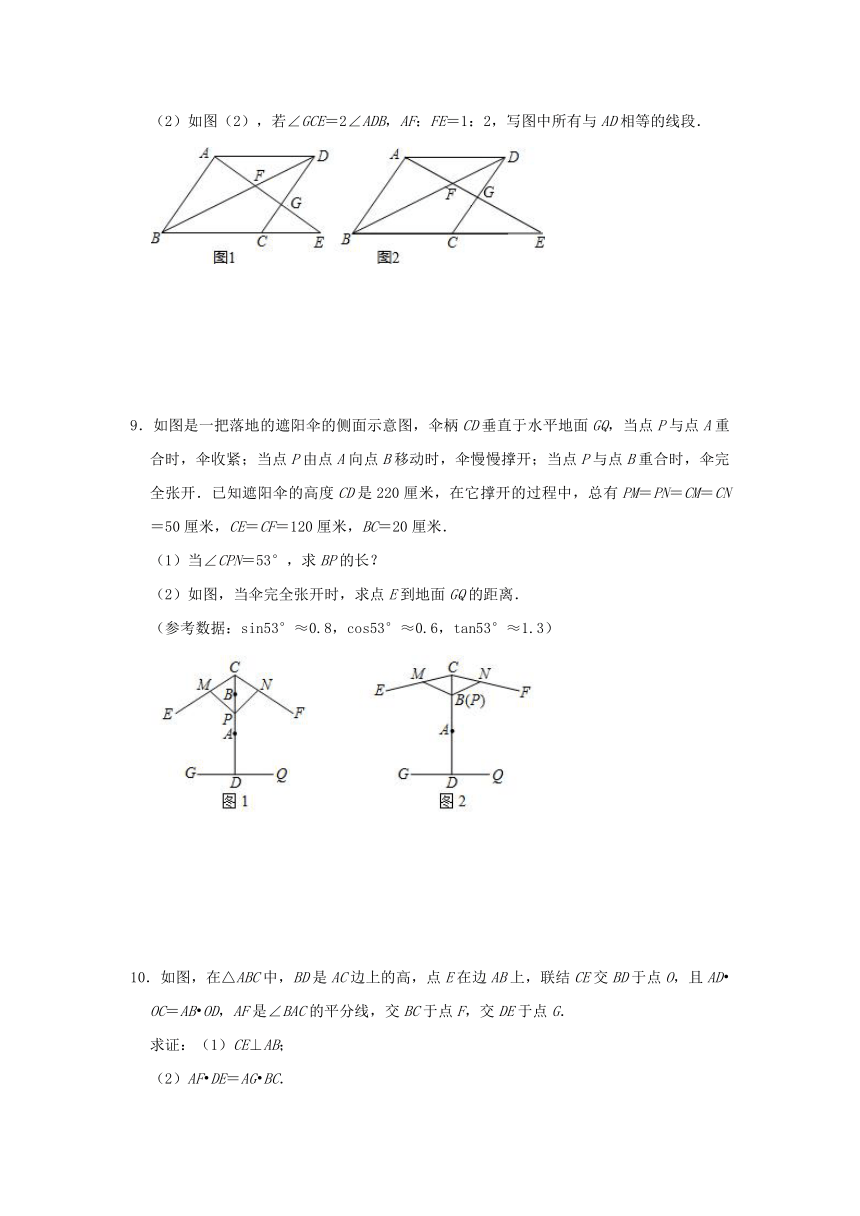
7.如图所示,在?ABCD中,AE:EB=1:2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6cm2,求S△CDF和S△ADF.
8.已知:?ABCD,点G在边DC上,直线AG交对角线BD于点F、交DC延长线于点E.
(1)如图(1),求证:△ABG∽△EDA;
(2)如图(2),若∠GCE=2∠ADB,AF:FE=1:2,写图中所有与AD相等的线段.
9.如图是一把落地的遮阳伞的侧面示意图,伞柄CD垂直于水平地面GQ,当点P与点A重合时,伞收紧;当点P由点A向点B移动时,伞慢慢撑开;当点P与点B重合时,伞完全张开.已知遮阳伞的高度CD是220厘米,在它撑开的过程中,总有PM=PN=CM=CN=50厘米,CE=CF=120厘米,BC=20厘米.
(1)当∠CPN=53°,求BP的长?
(2)如图,当伞完全张开时,求点E到地面GQ的距离.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
10.如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且AD?OC=AB?OD,AF是∠BAC的平分线,交BC于点F,交DE于点G.
求证:(1)CE⊥AB;
(2)AF?DE=AG?BC.
参考答案
1.(1)证明:方法一:
∵AB=AC,
∴∠B=∠BCA,
∵DF∥AC,
∴∠BFD=∠BCA,∠FDM=∠CEM,
∴∠B=∠BFD,
∴BD=FD,
方法二:
∵DF∥AC,
∴△BFD∽△BCA,
∵AB=AC,
∴BD=FD;
∵BD=CE,
∴DF=CE,
在△FDM和△CEM中,
,
∴△FDM≌△CEM(AAS),
∴FM=CM;
(2)解:∵BD=DF,DN⊥BC,
∴BN=FN,
∵FM=CM,
∴BC=BF+CF=2FN+2FM=2MN,
∵AB=AC=1,
∴BC===,
∴MN=BC=.
故答案为:.
2.证明:(1)∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠AED=∠ABD+∠BAE,∠BAF=∠MAN+∠BAE,∠MAN=∠ABD,
∴∠AED=∠BAF,
∴△AED∽△FAB,
∴,
即AD?AB=BF?DE,
∴AB2=BF?DE;
(2)∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∴△BME∽△DAE,
∴,
∵,
∴,
∴,
∴MN∥BD,
∴EF∥MN.
3.(1)证明:∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=,
∵∠A=∠A,
∴△ADC∽△AEB,
∴∠ABE=∠ACD;
(2)证明:∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDC=∠EBD,
∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,
()2=?,
∴.
4.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C的面积=4S△ABC=4(2×2﹣×1×1﹣×1×2﹣×1×2)=6.
5.解:(1)设HK=y,则AK=AH﹣KH=AH﹣EF=8﹣y,
∵四边形DEFG为矩形,
∴GF∥BC,
∴△AGF∽△ABC,
∴AK:AH=GF:BC,
∵当矩形DEFG是正方形时,GF=KH=y,
∴8﹣y:8=y:10,
解得:y=;
(2)设EF=x,则KH=x.
∴AK=AH﹣EF=8﹣x,
由(1)可知:,
解得:GF=10﹣x,
∴s=GF?EF=(10﹣x)x=﹣(x﹣4)2+20,
∴当x=4时S有最大值,并求出最大值20.
6.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t?(10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴=,即=,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴=,即=,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
7.解:(1)∵AE:EB=1:2,
∴AE:AB=1:3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF:C△CDF=EF:DF=AE:CD=AE:AB=1:3,
即△AEF与△CDF的周长比为1:3;
(2)∵△AEF∽△CDF,
∴S△AEF:S△CDF=(AE:CD)2,
即6:S△CDF=(1:3)2
∴S△CDF=6×9=54 cm2.
∵==,
∴S△ADF=3×6=18(cm2).
8.(1)证明:∵四边形ABCD是平行四边形,
∴∠ABG=∠EDA,AB∥DE,
∴∠BAG=∠DEA,
∴△ABG∽△EDA
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,
∴∠ADB=∠DBC,
∵∠GCE=2∠ADB=2∠DBC,
∵∠GCE=∠DBC+∠BDC,
∴∠DBC=∠BDC,
∴BC=CD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AD∥BC,
∴△ADF∽△BFE,
∴=,
∴AD=BE,
∴BC=CE,
∴与AD相等的线段有AB、BC、CD、CE.
9.解:(1)如图1中,连接MN交CD于H.
∵CM=MP=NC=NP=50cm,
∴四边形PMCN是菱形,
∴CP⊥NM,CH=PH,
∴PH=PN?cos53°≈30(cm),
∴PC=2PH=60cm,
∴PB=PC﹣BC=40cm.
(2)如图2中,连接MN交CD于J,连接EF交CD于H.
∵四边形CMBN是菱形,
∴CJ=JB=10cm,
∵MJ∥EH,
∴△CMJ∽△CEH,
∴=,
∴=,
∴CH=24,
∴HD=CD﹣CH=220﹣24=196cm,
∴当伞完全张开时,求点E到地面GQ的距离=HD=196cm.
10.证明:(1)∵AD?OC=AB?OD,
∴,
∵BD是AC边上的高,
∴∠BDC=∠BDA=90°,△ADB和△ODC是直角三角形,
∴Rt△ADB∽Rt△ODC,
∴∠ABD=∠OCD,
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,∠EOB+∠ABD+∠OEB=180°.
∴∠OEB=90°,
∴CE⊥AB;
(2)在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD=∠OCD,
∴△ADB∽△AEC,
∴,即,
在△DAE和△BAC中
∵∠DAE=∠BAC,.
∴△DAE∽△BAC,
∵AF是∠BAC的平分线,
∴,即AF?DE=AG?BC.
培优综合练
1.(1)拓展:如图①,在△ABC中,AB=AC,点D是AB上一点,点E是AC延长线上一点,且BD=CE.过点D作DF∥AC交BC于点F,连接DE交BC于点M.求证:BD=FD,FM=CM.
(2)应用:如图②,在上述“拓展”的条件下,另外增加条件∠A=90°,然后过点D作DN⊥BC,垂足为点N.若AC=1,则MN的长为 .
2.已知:如图,四边形ABCD是菱形,点M、N分别在边BC、CD上,联结AM、AN交对角线BD于E、F两点,且∠MAN=∠ABD.
(1)求证:AB2=BF?DE;
(2)若,求证:EF∥MN.
3.已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED=∠ABC,联结BE、CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:.
4.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A'B'C′.请在平面直角坐标系中画出△A'B'C';
(2)求出△A'B'C的面积.
5.如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
(1)当矩形DEFG是正方形时,求正方形的边长.
(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.
6.如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
7.如图所示,在?ABCD中,AE:EB=1:2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6cm2,求S△CDF和S△ADF.
8.已知:?ABCD,点G在边DC上,直线AG交对角线BD于点F、交DC延长线于点E.
(1)如图(1),求证:△ABG∽△EDA;
(2)如图(2),若∠GCE=2∠ADB,AF:FE=1:2,写图中所有与AD相等的线段.
9.如图是一把落地的遮阳伞的侧面示意图,伞柄CD垂直于水平地面GQ,当点P与点A重合时,伞收紧;当点P由点A向点B移动时,伞慢慢撑开;当点P与点B重合时,伞完全张开.已知遮阳伞的高度CD是220厘米,在它撑开的过程中,总有PM=PN=CM=CN=50厘米,CE=CF=120厘米,BC=20厘米.
(1)当∠CPN=53°,求BP的长?
(2)如图,当伞完全张开时,求点E到地面GQ的距离.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
10.如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且AD?OC=AB?OD,AF是∠BAC的平分线,交BC于点F,交DE于点G.
求证:(1)CE⊥AB;
(2)AF?DE=AG?BC.
参考答案
1.(1)证明:方法一:
∵AB=AC,
∴∠B=∠BCA,
∵DF∥AC,
∴∠BFD=∠BCA,∠FDM=∠CEM,
∴∠B=∠BFD,
∴BD=FD,
方法二:
∵DF∥AC,
∴△BFD∽△BCA,
∵AB=AC,
∴BD=FD;
∵BD=CE,
∴DF=CE,
在△FDM和△CEM中,
,
∴△FDM≌△CEM(AAS),
∴FM=CM;
(2)解:∵BD=DF,DN⊥BC,
∴BN=FN,
∵FM=CM,
∴BC=BF+CF=2FN+2FM=2MN,
∵AB=AC=1,
∴BC===,
∴MN=BC=.
故答案为:.
2.证明:(1)∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠AED=∠ABD+∠BAE,∠BAF=∠MAN+∠BAE,∠MAN=∠ABD,
∴∠AED=∠BAF,
∴△AED∽△FAB,
∴,
即AD?AB=BF?DE,
∴AB2=BF?DE;
(2)∵四边形ABCD是菱形,
∴AD=BC,AD∥BC,
∴△BME∽△DAE,
∴,
∵,
∴,
∴,
∴MN∥BD,
∴EF∥MN.
3.(1)证明:∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=,
∵∠A=∠A,
∴△ADC∽△AEB,
∴∠ABE=∠ACD;
(2)证明:∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDC=∠EBD,
∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,
()2=?,
∴.
4.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C的面积=4S△ABC=4(2×2﹣×1×1﹣×1×2﹣×1×2)=6.
5.解:(1)设HK=y,则AK=AH﹣KH=AH﹣EF=8﹣y,
∵四边形DEFG为矩形,
∴GF∥BC,
∴△AGF∽△ABC,
∴AK:AH=GF:BC,
∵当矩形DEFG是正方形时,GF=KH=y,
∴8﹣y:8=y:10,
解得:y=;
(2)设EF=x,则KH=x.
∴AK=AH﹣EF=8﹣x,
由(1)可知:,
解得:GF=10﹣x,
∴s=GF?EF=(10﹣x)x=﹣(x﹣4)2+20,
∴当x=4时S有最大值,并求出最大值20.
6.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t?(10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴=,即=,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴=,即=,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
7.解:(1)∵AE:EB=1:2,
∴AE:AB=1:3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF:C△CDF=EF:DF=AE:CD=AE:AB=1:3,
即△AEF与△CDF的周长比为1:3;
(2)∵△AEF∽△CDF,
∴S△AEF:S△CDF=(AE:CD)2,
即6:S△CDF=(1:3)2
∴S△CDF=6×9=54 cm2.
∵==,
∴S△ADF=3×6=18(cm2).
8.(1)证明:∵四边形ABCD是平行四边形,
∴∠ABG=∠EDA,AB∥DE,
∴∠BAG=∠DEA,
∴△ABG∽△EDA
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,
∴∠ADB=∠DBC,
∵∠GCE=2∠ADB=2∠DBC,
∵∠GCE=∠DBC+∠BDC,
∴∠DBC=∠BDC,
∴BC=CD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AD∥BC,
∴△ADF∽△BFE,
∴=,
∴AD=BE,
∴BC=CE,
∴与AD相等的线段有AB、BC、CD、CE.
9.解:(1)如图1中,连接MN交CD于H.
∵CM=MP=NC=NP=50cm,
∴四边形PMCN是菱形,
∴CP⊥NM,CH=PH,
∴PH=PN?cos53°≈30(cm),
∴PC=2PH=60cm,
∴PB=PC﹣BC=40cm.
(2)如图2中,连接MN交CD于J,连接EF交CD于H.
∵四边形CMBN是菱形,
∴CJ=JB=10cm,
∵MJ∥EH,
∴△CMJ∽△CEH,
∴=,
∴=,
∴CH=24,
∴HD=CD﹣CH=220﹣24=196cm,
∴当伞完全张开时,求点E到地面GQ的距离=HD=196cm.
10.证明:(1)∵AD?OC=AB?OD,
∴,
∵BD是AC边上的高,
∴∠BDC=∠BDA=90°,△ADB和△ODC是直角三角形,
∴Rt△ADB∽Rt△ODC,
∴∠ABD=∠OCD,
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,∠EOB+∠ABD+∠OEB=180°.
∴∠OEB=90°,
∴CE⊥AB;
(2)在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD=∠OCD,
∴△ADB∽△AEC,
∴,即,
在△DAE和△BAC中
∵∠DAE=∠BAC,.
∴△DAE∽△BAC,
∵AF是∠BAC的平分线,
∴,即AF?DE=AG?BC.
