第八章 平行线的性质与判定专项训练 (含解析)
文档属性
| 名称 | 第八章 平行线的性质与判定专项训练 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 20:40:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
平行线的性质与判定
类型一 平行线的判定
1.如图所示,下列条件能判定AB∥EF的是( )
A.∠B+∠BDC=180° B.∠CDE=∠BEF C.∠B=∠CDE D.∠B=∠BEF
2.如图所示,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
A.4组 B.3组 C.2组 D.1组
3.一种工件如图所示,要求AB∥CD,如果∠MGH=60°,再测出∠__________=60°或∠___________=120°,即可判断该工件合格.
类型二 平行线的性质
4.如图所示,将直尺与三角板叠放在一起,如果∠1=28°,那么∠2的度数为( )
A.62° B.56° C.28° D.72°
5.如图所示,梯子的各条横档互相平行,若∠1=∠2+20°,则∠3=___________.
类型三 平行线的判定与性质
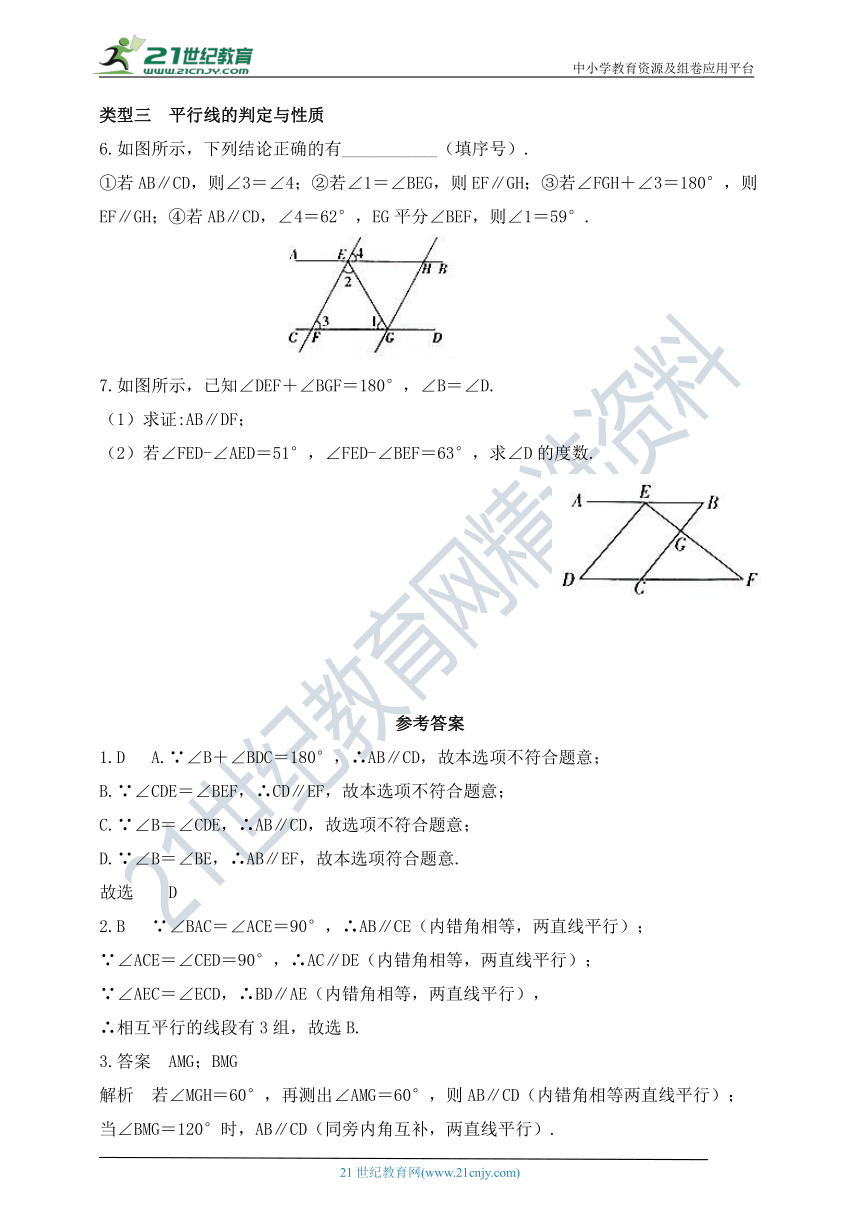
6.如图所示,下列结论正确的有___________(填序号).
①若AB∥CD,则∠3=∠4;②若∠1=∠BEG,则EF∥GH;③若∠FGH+∠3=180°,则EF∥GH;④若AB∥CD,∠4=62°,EG平分∠BEF,则∠1=59°.
7.如图所示,已知∠DEF+∠BGF=180°,∠B=∠D.
(1)求证:AB∥DF;
(2)若∠FED-∠AED=51°,∠FED-∠BEF=63°,求∠D的度数.
参考答案
1.D A.∵∠B+∠BDC=180°,∴AB∥CD,故本选项不符合题意;
B.∵∠CDE=∠BEF,∴CD∥EF,故本选项不符合题意;
C.∵∠B=∠CDE,∴AB∥CD,故选项不符合题意;
D.∵∠B=∠BE,∴AB∥EF,故本选项符合题意.
故选 D
2.B ∵∠BAC=∠ACE=90°,∴AB∥CE(内错角相等,两直线平行);
∵∠ACE=∠CED=90°,∴AC∥DE(内错角相等,两直线平行);
∵∠AEC=∠ECD,∴BD∥AE(内错角相等,两直线平行),
∴相互平行的线段有3组,故选B.
3.答案 AMG;BMG
解析 若∠MGH=60°,再测出∠AMG=60°,则AB∥CD(内错角相等两直线平行);
当∠BMG=120°时,AB∥CD(同旁内角互补,两直线平行).
4.A 如图,
由题意,得∠BAC=90°,∴∠DAC=∠BAC-∠1=62°,
∵EF∥AD,∴∠2=∠DAC=62°,
故选 A
5.答案 100°
解析 ∵AB∥CD,∴∠1=∠3,
又∵∠1=∠2+20°,∴∠3=∠2+20°,∴∠2=∠3-20°,
∵∠3+∠2=180°,∴∠3+∠3-20°=180°,
∴∠3=100°.
6.答案 ①③④
解析 ①若AB∥CD,则∠3=∠4,故结论正确;
②若∠1=∠BEG,则AB∥CD,故结论错误;
③若∠FGH+∠3=180°,则EF∥GH,故结论正确;
④∠BEF=180°-∠4=118°,∵EG平分∠BEF,∴∠2=59°,∵AB∥CD,∴∠3=∠4=62°,∴∠1=180°-∠2-∠3=59°,故结论正确故答案为①③④.
7.解析 (1)证明:∵∠DEF+∠BGF=180°,∠BGE+∠BGF=180°,∴∠DEF=∠BGE,
∵∠B+∠BGE+∠BEG=180°,∠D+∠DEF+∠F=180°,且∠B=∠D,
∴∠BEG=∠F,∴AB∥DF.
(2)设∠FED=x,
∵∠FED-∠AED=51°,∠FED-∠BEF=63°,∴∠AED=x-51°,∠BEF=x-63°,
∵∠AED+∠FED+∠BEF=180°,∴x-51°+x+x-63°=180°,∴x=98°,
∴∠AED=98°-51°=47°,∵AB∥DF,∴∠D=∠AED=47°.
_21?????????è?????(www.21cnjy.com)_
专项训练
平行线的性质与判定
类型一 平行线的判定
1.如图所示,下列条件能判定AB∥EF的是( )
A.∠B+∠BDC=180° B.∠CDE=∠BEF C.∠B=∠CDE D.∠B=∠BEF
2.如图所示,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
A.4组 B.3组 C.2组 D.1组
3.一种工件如图所示,要求AB∥CD,如果∠MGH=60°,再测出∠__________=60°或∠___________=120°,即可判断该工件合格.
类型二 平行线的性质
4.如图所示,将直尺与三角板叠放在一起,如果∠1=28°,那么∠2的度数为( )
A.62° B.56° C.28° D.72°
5.如图所示,梯子的各条横档互相平行,若∠1=∠2+20°,则∠3=___________.
类型三 平行线的判定与性质
6.如图所示,下列结论正确的有___________(填序号).
①若AB∥CD,则∠3=∠4;②若∠1=∠BEG,则EF∥GH;③若∠FGH+∠3=180°,则EF∥GH;④若AB∥CD,∠4=62°,EG平分∠BEF,则∠1=59°.
7.如图所示,已知∠DEF+∠BGF=180°,∠B=∠D.
(1)求证:AB∥DF;
(2)若∠FED-∠AED=51°,∠FED-∠BEF=63°,求∠D的度数.
参考答案
1.D A.∵∠B+∠BDC=180°,∴AB∥CD,故本选项不符合题意;
B.∵∠CDE=∠BEF,∴CD∥EF,故本选项不符合题意;
C.∵∠B=∠CDE,∴AB∥CD,故选项不符合题意;
D.∵∠B=∠BE,∴AB∥EF,故本选项符合题意.
故选 D
2.B ∵∠BAC=∠ACE=90°,∴AB∥CE(内错角相等,两直线平行);
∵∠ACE=∠CED=90°,∴AC∥DE(内错角相等,两直线平行);
∵∠AEC=∠ECD,∴BD∥AE(内错角相等,两直线平行),
∴相互平行的线段有3组,故选B.
3.答案 AMG;BMG
解析 若∠MGH=60°,再测出∠AMG=60°,则AB∥CD(内错角相等两直线平行);
当∠BMG=120°时,AB∥CD(同旁内角互补,两直线平行).
4.A 如图,
由题意,得∠BAC=90°,∴∠DAC=∠BAC-∠1=62°,
∵EF∥AD,∴∠2=∠DAC=62°,
故选 A
5.答案 100°
解析 ∵AB∥CD,∴∠1=∠3,
又∵∠1=∠2+20°,∴∠3=∠2+20°,∴∠2=∠3-20°,
∵∠3+∠2=180°,∴∠3+∠3-20°=180°,
∴∠3=100°.
6.答案 ①③④
解析 ①若AB∥CD,则∠3=∠4,故结论正确;
②若∠1=∠BEG,则AB∥CD,故结论错误;
③若∠FGH+∠3=180°,则EF∥GH,故结论正确;
④∠BEF=180°-∠4=118°,∵EG平分∠BEF,∴∠2=59°,∵AB∥CD,∴∠3=∠4=62°,∴∠1=180°-∠2-∠3=59°,故结论正确故答案为①③④.
7.解析 (1)证明:∵∠DEF+∠BGF=180°,∠BGE+∠BGF=180°,∴∠DEF=∠BGE,
∵∠B+∠BGE+∠BEG=180°,∠D+∠DEF+∠F=180°,且∠B=∠D,
∴∠BEG=∠F,∴AB∥DF.
(2)设∠FED=x,
∵∠FED-∠AED=51°,∠FED-∠BEF=63°,∴∠AED=x-51°,∠BEF=x-63°,
∵∠AED+∠FED+∠BEF=180°,∴x-51°+x+x-63°=180°,∴x=98°,
∴∠AED=98°-51°=47°,∵AB∥DF,∴∠D=∠AED=47°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
