2020-2021学年七年级数学苏科版下册《第7章 平面图形的认识(二)》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第7章 平面图形的认识(二)》单元测试卷(word有答案) |  | |
| 格式 | doc | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 23:09:45 | ||
图片预览




文档简介
2020-2021学年苏科新版七年级下册《第7章 平面图形的认识(二)》单元测试卷
一.选择题
1.如图,下列说法正确的有( )个.
①∠1和∠4是同位角;②∠1和∠5是同位角;③∠7和∠2是内错角;④∠1和∠4是同旁内角;⑤∠1和∠2是同旁内角.
A.1 B.2 C.3 D.4
2.如图:下列条件能说明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D C.∠B=∠C D.∠A+∠B=180°
3.如图,从学校到书店有两条路可走,请你判断下列说法正确的是( )
A.路①近? B.路②近 C.一样近 D.无法确定
4.已知:如图,AD是△ABC的角平分线,AE是△ABC的外角平分线,若∠DAC=20°,问∠EAC=( )
A.60° B.70° C.80° D.90°
5.有长度为9cm、12cm、15cm、36cm,39cm的五根木棒,从中任取三根,则可搭成(首尾连接)直角三角形的取法有( )
A.1种 B.2种 C.3种 D.4种
6.如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )
A.相等 B.互余 C.互补 D.不能确定
7.两条平行线被第三条直线所截,形成的角平分线互相平行的是( )
A.对顶角的角平分线 B.同位角的角平分线
C.同旁内角的角平分线 D.以上都不对
8.共有5个正三角形,从位置来看,下图中( )是由如图平移得到的.
A. B. C. D.
9.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
A.2011 B.2015 C.2014 D.2016
10.图中,可以视为是图形平移的不同组合对数(一个梅花对另一个梅花不计方向)有( )
A.9对 B.10对 C.5对 D.8对
二.填空题
11.将△ABC沿BC方向平移3cm得到△DEF,则CF= ;若∠A=80°,∠B=60°,则∠F= .
12.某校初一(3)班共有42名同学,若每两名同学互相握手一次.则每个同学需要握 次,全班同学共握手 次.
13.如图所示,∠ACD=115°,∠B=55°,则∠A= ,∠ACB= .
14.伸拉铁门能自由伸拉主要是应用了四边形的 .
15.△ABC的周长为24cm,a+b=2c,a:b=1:2,则a= ,b= ,c= .
16.如图,在△ABC中,BD=CD,∠ABE=∠CBE,则
(1) 是△ABC的中线,ED是△ 的中线;
(2)△ABC的角平分线是 ,BF是△ 的角平分线.
17.如图,DAE是一条直线,DE∥BC,则x= .
18.小明家买回一批地面砖,规格均为60cm×45cm,现欲在地面上铺成一个正方形的图案,至少要用 块地砖.
19.如图,求∠A+∠B+∠C+∠D+∠E+∠F= .
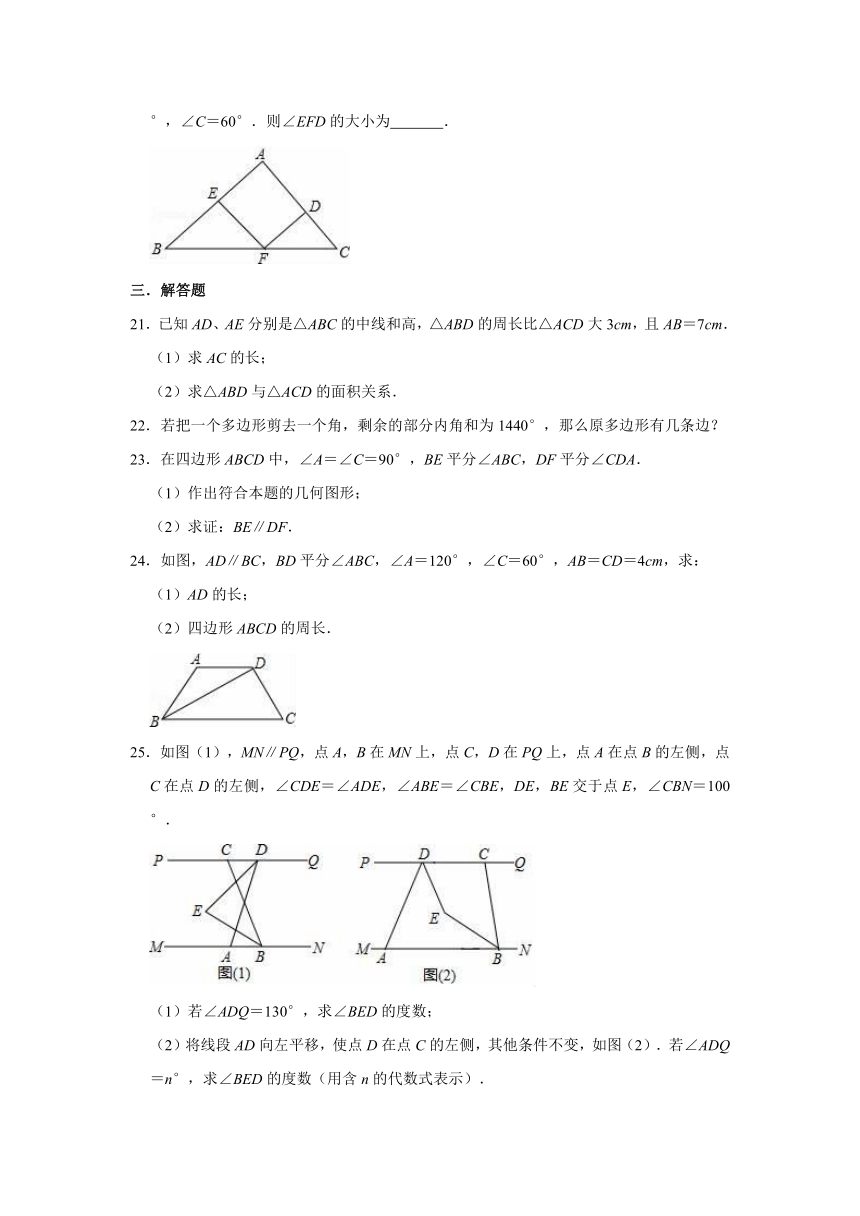
20.如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD的大小为 .
三.解答题
21.已知AD、AE分别是△ABC的中线和高,△ABD的周长比△ACD大3cm,且AB=7cm.
(1)求AC的长;
(2)求△ABD与△ACD的面积关系.
22.若把一个多边形剪去一个角,剩余的部分内角和为1440°,那么原多边形有几条边?
23.在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)作出符合本题的几何图形;
(2)求证:BE∥DF.
24.如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,AB=CD=4cm,求:
(1)AD的长;
(2)四边形ABCD的周长.
25.如图(1),MN∥PQ,点A,B在MN上,点C,D在PQ上,点A在点B的左侧,点C在点D的左侧,∠CDE=∠ADE,∠ABE=∠CBE,DE,BE交于点E,∠CBN=100°.
(1)若∠ADQ=130°,求∠BED的度数;
(2)将线段AD向左平移,使点D在点C的左侧,其他条件不变,如图(2).若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).
参考答案与试题解析
一.选择题
1.解:①∠1和∠4找不到被截线,不是同位角,故错误;
②∠1和∠5在截线的同一方,被截线的同一侧是同位角,故正确;
③∠7和∠2找不到被截线,不是内错角,故错误;
④∠1和∠4找不到被截线,不是同旁内角,故错误;
⑤∠1和∠2在截线的内部,被截线的同侧是同旁内角,故正确.
根据同位角、内错角、同旁内角的定义,正确的是②⑤两个,
故选:B.
2.解:∵∠A+∠B=180°,
∴AD∥BC.
故选:D.
3.解:根据平移的性质得出:从学校到书店有两条路一样近.
故选:C.
4.解:∵AD是△ABC的角平分线,∠DAC=20°,
∴∠BAC=2∠DAC=40°,
∴∠B+∠ACD=140°,
∴∠EAC=∠FAC=(∠B+∠ACD)=70°.
故选:B.
5.解:∵92=81,122=144,152=225,362=1296,392=1521,
又∵81+144=225,225+1296=1521,
∴92+122=152,152+362=392,
故选:B.
6.解:∵AB∥CD,
∴∠B=∠C,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠D=180°,
∵CD∥EF,
∴∠D=∠E,
∴∠B+∠E=180°,即∠B和∠E互补.
故选:C.
7.解:A、对顶角的角平分线AC、AD共线,故错误;
B、同位角的角平分线AC、BF互相平行,
∵AM∥BN,∴∠PAM=∠PBN;
∵AC、BF是∠PAM和∠PBN的角平分线,
∴∠1=∠PAM=∠PBN=∠2;
∴AC∥BF.故正确.
C、同旁内角的角平分线AE、BF互相垂直,
∵AM∥BN,∴∠MAB+∠PBN=180°;
∵AE、BF是∠MAB和∠PBN的角平分线,
∴∠3+∠2=∠MAB+∠PBN=90°;
∴AE⊥BF.故错误.
D、因为B正确,所以错误.
故选:B.
8.解:A、可以由对称得到;
B、可以由平移得到;
C、可以由旋转变换得到;
D、可以由旋转变换得到;
故选:B.
9.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为2013+1=2014.
故选:C.
10.解:1和2、3、4、5有四种组合;2和3、4、5有三种组合;3和4、5有两种组合;4和5有一种组合,共有4+3+2+1=10中组合.
故选:B.
二.填空题
11.解:观察图形可知,对应点连接的线段是AD、BE和CF.
∵△ABC沿BC方向平移3cm得到△DEF,
∴BE=CF=3cm,
∴∠F=∠ACB=180°﹣∠A﹣∠B=40°,
故答案为:3cm,40°.
12.解:∵共有42名同学,若每两名同学互相握手一次,
∴每个同学需要握41次,
全班同学共握手41×42÷2=861(次),
故答案为:41;861.
13.解:∵∠ACD为△ABC的外角,
∴∠ACD=∠A+∠B,
则∠B=115°﹣55°=60°,
又∠ACB和∠ACD互为邻补角,
∴∠ACB=180°﹣∠ACD=180°﹣115°=65°.
故答案为:60°,65°.
14.解:伸拉铁门能自由伸拉主要是应用了四边形的不稳定性.
故空中填:不稳定性.
15.解:根据题意,得
,
解得.
故答案分别是:,,8.
16.解:(1)∵BD=CD,
∴AD是△ABC的中线,ED是△BEC的中线;
(2)∵∠ABE=∠CBE,
∴△ABC的角平分线是BE,BF是△ABD的角平分线.
故答案为:(1)AD;BEC;(2)BE;ABD.
17.解:∵DE∥BC,
∴∠DAC=∠ACF,
即70°+x=134°,
解得x=64°.
故答案为:64°.
18.解:∵60和45的最大公约数是15,
∴60÷15×(45÷15)=12块,
故答案为:12.
19.解:∵∠1=∠A+∠B,∠2=∠D+∠E,
又∵∠1+∠F=115°,∠2+∠C=115°,
∴∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°.
故答案为:230°.
20.解:∵在△ABC中,∠B=45°,∠C=60°,
∴∠A=180°﹣∠B﹣∠C=180°﹣45°﹣60°=75°.
∵EF∥AC,DF∥AB,
∴四边形AEFD是平行四边形,
∴∠EFD=∠A=75°.
故答案为:75°.
三.解答题
21.解:(1)∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD大3cm,
∴AB+BD+AD﹣(AD+AC+DC)=3cm,
AB﹣AC=3cm,
∵AB=7cm,
∴AC=4cm;
(2)△ABD与△ACD的面积相等;
∵S△ADB=DB?AE,S△ADC=DC?AE,
∴S△ADB=S△ADC.
22.解:设新多边形是n边形,由多边形内角和公式得(n﹣2)×180°=1440°,
解得n=10,
原多边形是10﹣1=9,10+1=11,
故答案为:9、10或11.
23.(1)解:如图所示:
(2)证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠CDA,
∴∠ADF=∠FDE=ADC,∠EBF=∠EBC=ABC,
∴∠FBE+∠FDE=90°,
∵∠A=90°,
∴∠AFD+∠ADF=90°,
∴∠AFD+∠EDF=90°,
∴∠DFA=∠EBF,
∴DF∥EB.
24.(1)解:∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AD=AB=4cm;
(2)解:∵AD∥BC,∠A=120°,∠C=60°,
∴∠ADC=120°,∠ABC=60°,∠ADB=∠DBC;
∵BD平分∠ABC,∴∠ABD=∠ADB=30°,∠BDC=90°;
∴AB=AD,BC=2CD;又AB=CD=4cm,
∴AD=4,BC=8,
∴AB+BC+CD+AD=4+8+4+4=20(cm),
∴四边形ABCD的周长为20cm.
25.解:(1)如图(1),过点E作EF∥PQ.
∵∠CBN=100°,∠ADQ=130°,
∴∠CBM=80°,∠ADP=50°.
∵∠CDE=∠ADE,∠ABE=∠CBE,
∴∠EBM=40°,∠EDP=25°.
∵EF∥PQ,
∴∠DEF=∠EDP=25°.
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=∠DEF+∠FEB=25°+40°=65°;
(2)如图(2),过点E作EF∥PQ.
∵∠CBN=100°,
∴∠CBM=80°.
∵∠CDE=∠ADE,∠ABE=∠CBE,
∴∠EBM=40°,∠EDQ=n°.
∵EF∥PQ,
∴∠DEF=180°﹣∠EDQ=180°﹣n°.
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=∠DEF+∠FEB=180°﹣n°+40°=220°﹣n°.
一.选择题
1.如图,下列说法正确的有( )个.
①∠1和∠4是同位角;②∠1和∠5是同位角;③∠7和∠2是内错角;④∠1和∠4是同旁内角;⑤∠1和∠2是同旁内角.
A.1 B.2 C.3 D.4
2.如图:下列条件能说明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D C.∠B=∠C D.∠A+∠B=180°
3.如图,从学校到书店有两条路可走,请你判断下列说法正确的是( )
A.路①近? B.路②近 C.一样近 D.无法确定
4.已知:如图,AD是△ABC的角平分线,AE是△ABC的外角平分线,若∠DAC=20°,问∠EAC=( )
A.60° B.70° C.80° D.90°
5.有长度为9cm、12cm、15cm、36cm,39cm的五根木棒,从中任取三根,则可搭成(首尾连接)直角三角形的取法有( )
A.1种 B.2种 C.3种 D.4种
6.如图,AB∥CD∥EF,BC∥DE,则∠B与∠E的关系是( )
A.相等 B.互余 C.互补 D.不能确定
7.两条平行线被第三条直线所截,形成的角平分线互相平行的是( )
A.对顶角的角平分线 B.同位角的角平分线
C.同旁内角的角平分线 D.以上都不对
8.共有5个正三角形,从位置来看,下图中( )是由如图平移得到的.
A. B. C. D.
9.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
A.2011 B.2015 C.2014 D.2016
10.图中,可以视为是图形平移的不同组合对数(一个梅花对另一个梅花不计方向)有( )
A.9对 B.10对 C.5对 D.8对
二.填空题
11.将△ABC沿BC方向平移3cm得到△DEF,则CF= ;若∠A=80°,∠B=60°,则∠F= .
12.某校初一(3)班共有42名同学,若每两名同学互相握手一次.则每个同学需要握 次,全班同学共握手 次.
13.如图所示,∠ACD=115°,∠B=55°,则∠A= ,∠ACB= .
14.伸拉铁门能自由伸拉主要是应用了四边形的 .
15.△ABC的周长为24cm,a+b=2c,a:b=1:2,则a= ,b= ,c= .
16.如图,在△ABC中,BD=CD,∠ABE=∠CBE,则
(1) 是△ABC的中线,ED是△ 的中线;
(2)△ABC的角平分线是 ,BF是△ 的角平分线.
17.如图,DAE是一条直线,DE∥BC,则x= .
18.小明家买回一批地面砖,规格均为60cm×45cm,现欲在地面上铺成一个正方形的图案,至少要用 块地砖.
19.如图,求∠A+∠B+∠C+∠D+∠E+∠F= .
20.如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD的大小为 .
三.解答题
21.已知AD、AE分别是△ABC的中线和高,△ABD的周长比△ACD大3cm,且AB=7cm.
(1)求AC的长;
(2)求△ABD与△ACD的面积关系.
22.若把一个多边形剪去一个角,剩余的部分内角和为1440°,那么原多边形有几条边?
23.在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)作出符合本题的几何图形;
(2)求证:BE∥DF.
24.如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,AB=CD=4cm,求:
(1)AD的长;
(2)四边形ABCD的周长.
25.如图(1),MN∥PQ,点A,B在MN上,点C,D在PQ上,点A在点B的左侧,点C在点D的左侧,∠CDE=∠ADE,∠ABE=∠CBE,DE,BE交于点E,∠CBN=100°.
(1)若∠ADQ=130°,求∠BED的度数;
(2)将线段AD向左平移,使点D在点C的左侧,其他条件不变,如图(2).若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).
参考答案与试题解析
一.选择题
1.解:①∠1和∠4找不到被截线,不是同位角,故错误;
②∠1和∠5在截线的同一方,被截线的同一侧是同位角,故正确;
③∠7和∠2找不到被截线,不是内错角,故错误;
④∠1和∠4找不到被截线,不是同旁内角,故错误;
⑤∠1和∠2在截线的内部,被截线的同侧是同旁内角,故正确.
根据同位角、内错角、同旁内角的定义,正确的是②⑤两个,
故选:B.
2.解:∵∠A+∠B=180°,
∴AD∥BC.
故选:D.
3.解:根据平移的性质得出:从学校到书店有两条路一样近.
故选:C.
4.解:∵AD是△ABC的角平分线,∠DAC=20°,
∴∠BAC=2∠DAC=40°,
∴∠B+∠ACD=140°,
∴∠EAC=∠FAC=(∠B+∠ACD)=70°.
故选:B.
5.解:∵92=81,122=144,152=225,362=1296,392=1521,
又∵81+144=225,225+1296=1521,
∴92+122=152,152+362=392,
故选:B.
6.解:∵AB∥CD,
∴∠B=∠C,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠D=180°,
∵CD∥EF,
∴∠D=∠E,
∴∠B+∠E=180°,即∠B和∠E互补.
故选:C.
7.解:A、对顶角的角平分线AC、AD共线,故错误;
B、同位角的角平分线AC、BF互相平行,
∵AM∥BN,∴∠PAM=∠PBN;
∵AC、BF是∠PAM和∠PBN的角平分线,
∴∠1=∠PAM=∠PBN=∠2;
∴AC∥BF.故正确.
C、同旁内角的角平分线AE、BF互相垂直,
∵AM∥BN,∴∠MAB+∠PBN=180°;
∵AE、BF是∠MAB和∠PBN的角平分线,
∴∠3+∠2=∠MAB+∠PBN=90°;
∴AE⊥BF.故错误.
D、因为B正确,所以错误.
故选:B.
8.解:A、可以由对称得到;
B、可以由平移得到;
C、可以由旋转变换得到;
D、可以由旋转变换得到;
故选:B.
9.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为2013+1=2014.
故选:C.
10.解:1和2、3、4、5有四种组合;2和3、4、5有三种组合;3和4、5有两种组合;4和5有一种组合,共有4+3+2+1=10中组合.
故选:B.
二.填空题
11.解:观察图形可知,对应点连接的线段是AD、BE和CF.
∵△ABC沿BC方向平移3cm得到△DEF,
∴BE=CF=3cm,
∴∠F=∠ACB=180°﹣∠A﹣∠B=40°,
故答案为:3cm,40°.
12.解:∵共有42名同学,若每两名同学互相握手一次,
∴每个同学需要握41次,
全班同学共握手41×42÷2=861(次),
故答案为:41;861.
13.解:∵∠ACD为△ABC的外角,
∴∠ACD=∠A+∠B,
则∠B=115°﹣55°=60°,
又∠ACB和∠ACD互为邻补角,
∴∠ACB=180°﹣∠ACD=180°﹣115°=65°.
故答案为:60°,65°.
14.解:伸拉铁门能自由伸拉主要是应用了四边形的不稳定性.
故空中填:不稳定性.
15.解:根据题意,得
,
解得.
故答案分别是:,,8.
16.解:(1)∵BD=CD,
∴AD是△ABC的中线,ED是△BEC的中线;
(2)∵∠ABE=∠CBE,
∴△ABC的角平分线是BE,BF是△ABD的角平分线.
故答案为:(1)AD;BEC;(2)BE;ABD.
17.解:∵DE∥BC,
∴∠DAC=∠ACF,
即70°+x=134°,
解得x=64°.
故答案为:64°.
18.解:∵60和45的最大公约数是15,
∴60÷15×(45÷15)=12块,
故答案为:12.
19.解:∵∠1=∠A+∠B,∠2=∠D+∠E,
又∵∠1+∠F=115°,∠2+∠C=115°,
∴∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°.
故答案为:230°.
20.解:∵在△ABC中,∠B=45°,∠C=60°,
∴∠A=180°﹣∠B﹣∠C=180°﹣45°﹣60°=75°.
∵EF∥AC,DF∥AB,
∴四边形AEFD是平行四边形,
∴∠EFD=∠A=75°.
故答案为:75°.
三.解答题
21.解:(1)∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长比△ACD大3cm,
∴AB+BD+AD﹣(AD+AC+DC)=3cm,
AB﹣AC=3cm,
∵AB=7cm,
∴AC=4cm;
(2)△ABD与△ACD的面积相等;
∵S△ADB=DB?AE,S△ADC=DC?AE,
∴S△ADB=S△ADC.
22.解:设新多边形是n边形,由多边形内角和公式得(n﹣2)×180°=1440°,
解得n=10,
原多边形是10﹣1=9,10+1=11,
故答案为:9、10或11.
23.(1)解:如图所示:
(2)证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠CDA,
∴∠ADF=∠FDE=ADC,∠EBF=∠EBC=ABC,
∴∠FBE+∠FDE=90°,
∵∠A=90°,
∴∠AFD+∠ADF=90°,
∴∠AFD+∠EDF=90°,
∴∠DFA=∠EBF,
∴DF∥EB.
24.(1)解:∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AD=AB=4cm;
(2)解:∵AD∥BC,∠A=120°,∠C=60°,
∴∠ADC=120°,∠ABC=60°,∠ADB=∠DBC;
∵BD平分∠ABC,∴∠ABD=∠ADB=30°,∠BDC=90°;
∴AB=AD,BC=2CD;又AB=CD=4cm,
∴AD=4,BC=8,
∴AB+BC+CD+AD=4+8+4+4=20(cm),
∴四边形ABCD的周长为20cm.
25.解:(1)如图(1),过点E作EF∥PQ.
∵∠CBN=100°,∠ADQ=130°,
∴∠CBM=80°,∠ADP=50°.
∵∠CDE=∠ADE,∠ABE=∠CBE,
∴∠EBM=40°,∠EDP=25°.
∵EF∥PQ,
∴∠DEF=∠EDP=25°.
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=∠DEF+∠FEB=25°+40°=65°;
(2)如图(2),过点E作EF∥PQ.
∵∠CBN=100°,
∴∠CBM=80°.
∵∠CDE=∠ADE,∠ABE=∠CBE,
∴∠EBM=40°,∠EDQ=n°.
∵EF∥PQ,
∴∠DEF=180°﹣∠EDQ=180°﹣n°.
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=∠DEF+∠FEB=180°﹣n°+40°=220°﹣n°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
