2020-2021学年人教新版九年级下册数学《第27章 相似》单元测试卷(word解析版)
文档属性
| 名称 | 2020-2021学年人教新版九年级下册数学《第27章 相似》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 23:18:57 | ||
图片预览


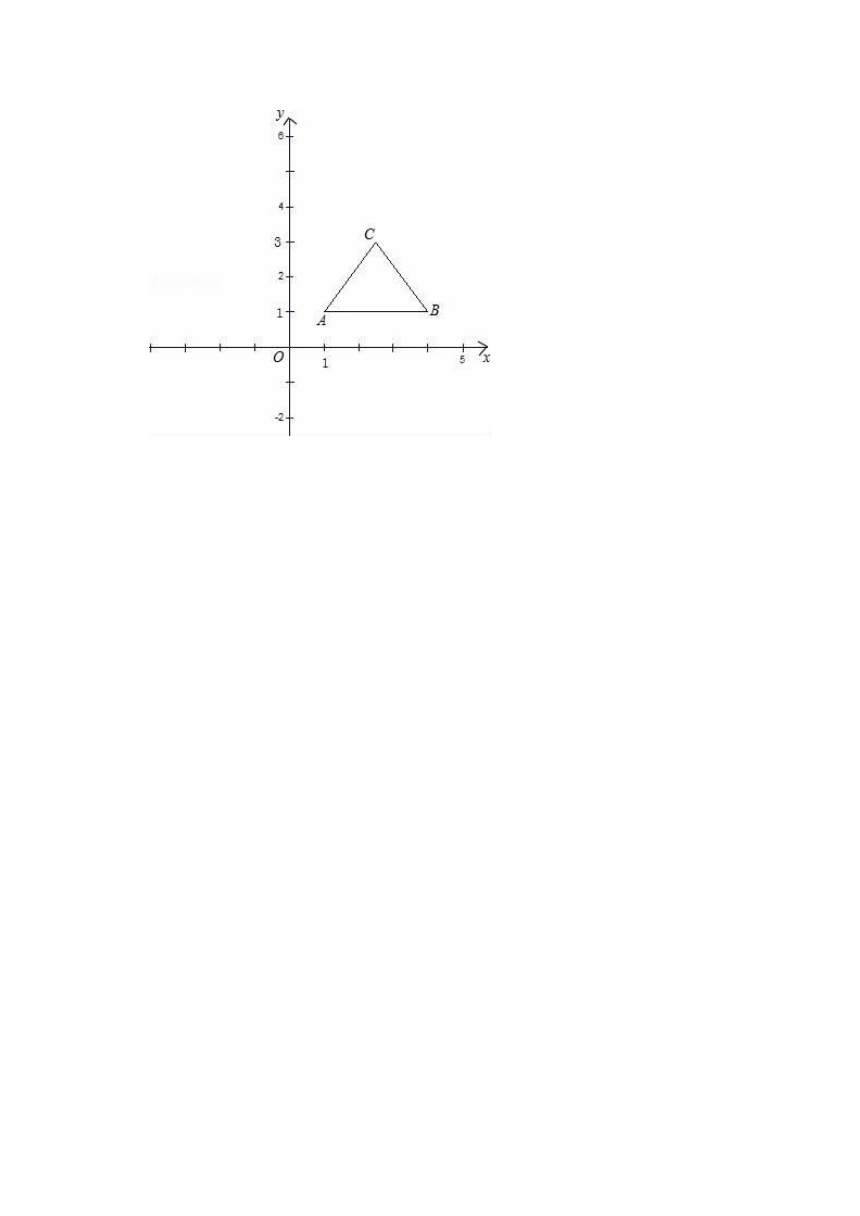
文档简介
2020-2021学年人教新版九年级下册数学《第27章
相似》单元测试卷
一.选择题
1.把ad=bc写成比例式,错误的是( )
A.a:b=c:d
B.b:d=a:c
C.b:a=d:c
D.b:d=c:a
2.下列语句中的图形必成相似形的是( )
A.只有一个角为30°的等腰三角形
B.邻边之比为2的两个平行四边形
C.底角为40°的两个等腰梯形
D.有一个角为40°的两个等腰梯形
3.两个相似三角形的相似比是,其中较小的三角形的面积是14cm2,则较大三角形的面积是( )
A.10cm2
B.
cm2
C.
cm2
D.
cm2
4.△ABC和△DEF满足下列条件,其中使△ABC与△DEF不相似的是( )
A.∠A=∠D=45°32′,∠C=26°28′,∠E=108°
B.BC=a,AC=b,AB=c,DE=,EF=,DF=
C.AB=1,AC=1.5,BC=2,DE=12,EF=24,DF=18
D.AB=AC,DE=DF,∠A=∠D=50°
5.在Rt△ABC中,∠A=15°,∠C=90°,则斜边上的高与斜边的比为( )
A.1:2
B.1:3
C.1:4
D.1:6
6.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
7.梯形ABCD中,AD∥BC,AD=a,BC=b,EF∥AD交AB,CD于E,F,且梯形AEFD与梯形EBCF相似,则EF等于( )
A.
B.
C.
D.不能确定
8.如图,AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3等于( )
A.45°
B.60°
C.75°
D.90°
9.已知甲、乙两地图的比例尺分别为1:5000和1:20
000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2
B.2:5
C.1:4
D.4:1
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,那么所得的图形与原图形相比( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
二.填空题
11.某一时刻,一根4米长的旗杆的影子长6米,同一时刻一座建筑物的影子长36米,则这座建筑物的高度为
米.
12.长方形地基,长75米,宽30米,把它画在比例尺是1:100的图纸上,长应是
cm,宽应是
cm.
13.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
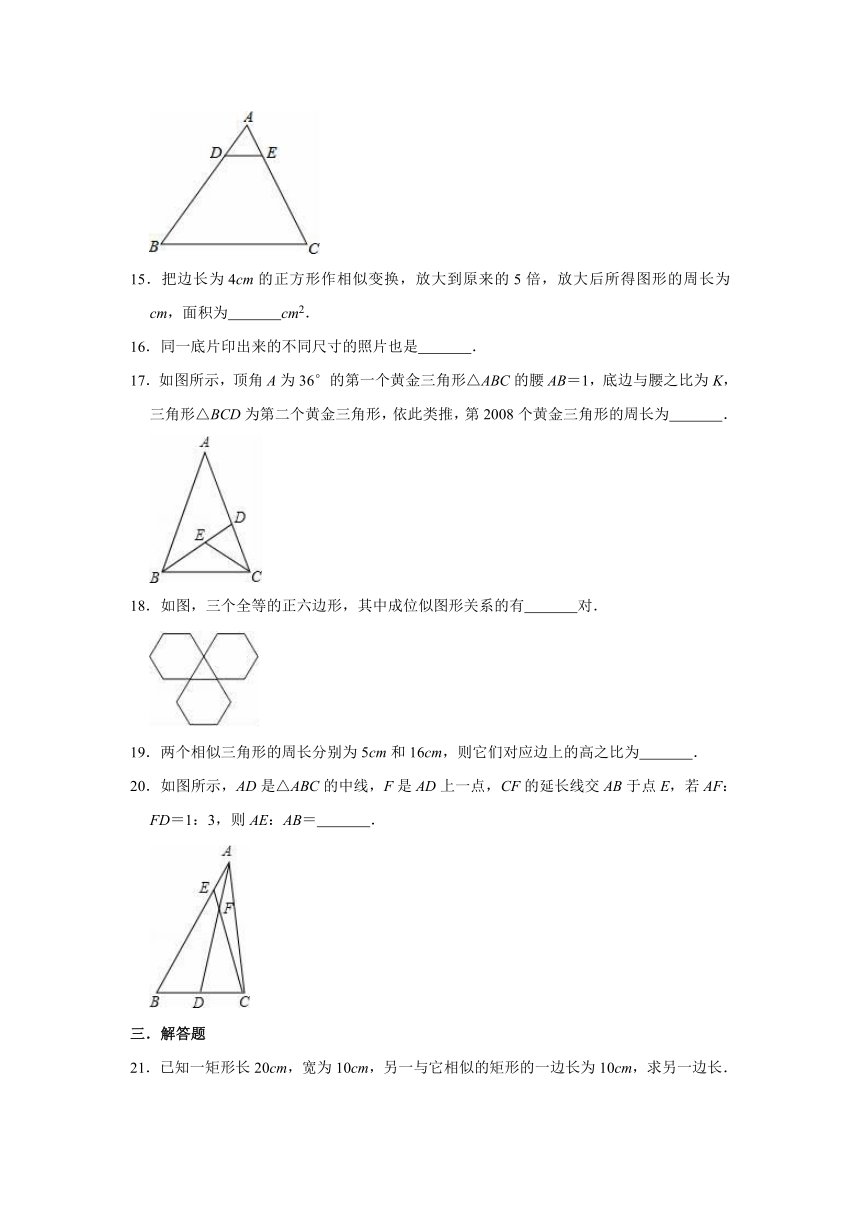
14.如图,在△ABC中,DE∥BC,AD=1cm,BD=5cm,BC=6cm,则DE=
cm.
15.把边长为4cm的正方形作相似变换,放大到原来的5倍,放大后所得图形的周长为
cm,面积为
cm2.
16.同一底片印出来的不同尺寸的照片也是
.
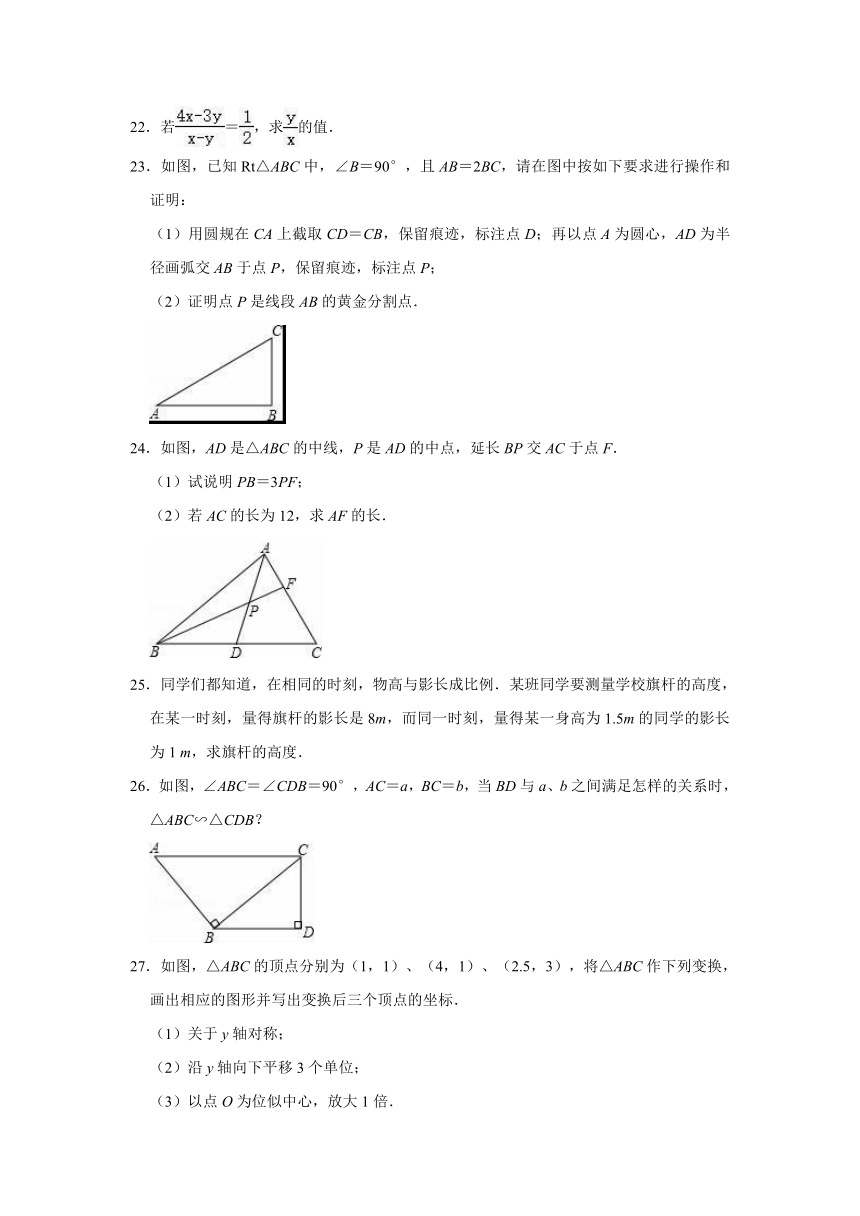
17.如图所示,顶角A为36°的第一个黄金三角形△ABC的腰AB=1,底边与腰之比为K,三角形△BCD为第二个黄金三角形,依此类推,第2008个黄金三角形的周长为
.
18.如图,三个全等的正六边形,其中成位似图形关系的有
对.
19.两个相似三角形的周长分别为5cm和16cm,则它们对应边上的高之比为
.
20.如图所示,AD是△ABC的中线,F是AD上一点,CF的延长线交AB于点E,若AF:FD=1:3,则AE:AB=
.
三.解答题
21.已知一矩形长20cm,宽为10cm,另一与它相似的矩形的一边长为10cm,求另一边长.
22.若=,求的值.
23.如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:
(1)用圆规在CA上截取CD=CB,保留痕迹,标注点D;再以点A为圆心,AD为半径画弧交AB于点P,保留痕迹,标注点P;
(2)证明点P是线段AB的黄金分割点.
24.如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
25.同学们都知道,在相同的时刻,物高与影长成比例.某班同学要测量学校旗杆的高度,在某一时刻,量得旗杆的影长是8m,而同一时刻,量得某一身高为1.5m的同学的影长为1
m,求旗杆的高度.
26.如图,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?
27.如图,△ABC的顶点分别为(1,1)、(4,1)、(2.5,3),将△ABC作下列变换,画出相应的图形并写出变换后三个顶点的坐标.
(1)关于y轴对称;
(2)沿y轴向下平移3个单位;
(3)以点O为位似中心,放大1倍.
参考答案与试题解析
一.选择题
1.解:∵ad=bc,
∴写成比例式为:a:b=c:d、b:d=a:c、b:a=d:c,
故选:D.
2.解:A、只有一个角为30°的等腰三角形,30°的角必定是顶角,所以,底角也一定相等,三角形相似,故本选项正确;
B、邻边之比为2,夹角不一定相等,两平行四边形不一定相似,故本选项错误;
C、底角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误;
D、有一个角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误.
故选:A.
3.解:∵两个相似三角形的相似比是,
∴S大三角形:S小三角形=()2=,
又∵S小三角形=14,
∴S大三角形=Cm2.
故选:D.
4.解:A、中三个角对应相等,所以两个三角形相似;
B、中对应边不成比例,所以不能判定其相似,B不正确;
C、∵AB=1,AC=1.5,BC=2,DE=12,EF=24,DF=18,
∴,即==,
故即对应边成比例,C对;
D、中两边与一角,求是两边的夹角,所以D对.
故选:B.
5.解:设斜边AB上的高为CD,垂足为D,
∴sinA=,
∴AB==,
∵cos∠DCB=cos15°=,
∴CD=cos15?BC,
∴==,
故选:C.
6.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
7.解:梯形AEFD与梯形EBCF相似,
则对应边的比相等,
因而得到:AD:EF=EF:BC
即a:EF=EF:b,
则EF2=ab
∴EF=.
故选:A.
8.解:∵AB=BC,∠B=90°,∴∠1=45°.
设AB=BC=CD=DE=1,则AC=,CE=2,
∴,
∴△ACE∽△DCA,∴∠2=∠CAE.
∵∠1=∠CAE+∠3=∠2+∠3,
∴∠1+∠2+∠3=90°.
故选:D.
9.解:把图上距离看作单位1,设A、B和C、D两地的实际距离分别为x和y,则:
1:5000=1:x,
解得x=5000,
1:20000=1:y,
解得y=20000,
∴x:y=5000:20000=1:4.
故选:C.
10.解:∵一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,
∴整个图形被纵向压缩为原来的一半
故选:D.
二.填空题
11.解:设建筑物高为x,根据在同一时刻同一地点任何物体的高与其影子长的比值相同得,
∴x=24,
∴建筑物的高为24米,
故答案为:24.
12.解:根据图上距离=实际距离×比例尺,
得图上长应是75×=0.75m=75cm,
宽应是30×=0.3m=30cm.
13.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
14.解:如图,∵AD=1cm,BD=5cm,
∴AB=AD+BD=6cm.
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
则ED=1cm.
故答案是:1.
15.解:放大5倍,即边长变为20,
所以周长为20×4=80cm;
面积为20×20=400cm2
16.解:同一底片印出来的不同尺寸的照片,形状相同,但大小不同,∴是相似图形.
17.解:第一个三角形的周长为K+2;
第二个三角形的周长K+K+K2=K(K+2);
第三个周长为K2+K2+K3=K2(K+2)
…
所以第2008个三角形的周长为K2007(K+2)
18.解:成位似图形关系的有3对.
19.解:已知两个相似三角形的周长分别为5cm和16cm,
则它们的相似比是5:16,
那么它们对应边上的高之比为5:16.
故答案为:5:16.
20.解:∵AF:FD=1:3
∴
作DG∥CE,交AB于点G
∵D是BC的中点
∴EC=2DG
∴
∴EF=DG
∴
∴AG=4AE
∴EG=BG=3AE
∴AB=7AE
∴AE:AB=1:7.
三.解答题
21.解:设另一边是xcm.
当所求的边与20cm的边是对应边时,根据题意得:20:10=x:10
解得:x=20cm;
当所求的边与10cm的边是对应边时,根据题意得20:10=10:x
解得:x=5cm;
因而另一边长长是20cm或5cm.
22.解:∵=,
∴8x﹣6y=x﹣y,
x=,
∴==.
23.解:(1)如图所示:
(2)设BC=x,则AB=2x,AC=x,
由题意得,CD=x,
则AP=AD=(﹣1)x,
=,
则点P是线段AB的黄金分割点.
24.解:(1)过D作DE∥AC,交BF于点E,
∴∠PDE=∠PAF,
∵P是AD的中点,
∴AP=DP,
∵在△PDE和△PAF中,
,
∴△PDE≌△PAF(ASA),
∴PE=PF,
由DE∥AC,得到=,
∵AD是△ABC的中线,
∴BD=DC,
∴BE=EF=2PF,
∴BP=3PF;
(2)∵△PDE≌△PAF,
∴DE=AF,
∴==,
∴AF=AC=×12=4.
25.解:∵物高与影长成比例,
∴旗杆的高度:8=1.5:1,
∴旗杆的高度=1.5×8=12米.
答:旗杆的高度是12米.
26.解:若△ABC∽△CDB,则有=,
即=,∴BD=,
当BD=时,△ABC∽△CDB.
27.解:
(1)A1(﹣1,1)、B1(﹣4,1)、C1、(2.5,3);
(2)A2(1,﹣2)、B2(4,﹣2)、C2(2.5,0);
(3)A3(2,2)、B3(8,2)、C3(5,6).
相似》单元测试卷
一.选择题
1.把ad=bc写成比例式,错误的是( )
A.a:b=c:d
B.b:d=a:c
C.b:a=d:c
D.b:d=c:a
2.下列语句中的图形必成相似形的是( )
A.只有一个角为30°的等腰三角形
B.邻边之比为2的两个平行四边形
C.底角为40°的两个等腰梯形
D.有一个角为40°的两个等腰梯形
3.两个相似三角形的相似比是,其中较小的三角形的面积是14cm2,则较大三角形的面积是( )
A.10cm2
B.
cm2
C.
cm2
D.
cm2
4.△ABC和△DEF满足下列条件,其中使△ABC与△DEF不相似的是( )
A.∠A=∠D=45°32′,∠C=26°28′,∠E=108°
B.BC=a,AC=b,AB=c,DE=,EF=,DF=
C.AB=1,AC=1.5,BC=2,DE=12,EF=24,DF=18
D.AB=AC,DE=DF,∠A=∠D=50°
5.在Rt△ABC中,∠A=15°,∠C=90°,则斜边上的高与斜边的比为( )
A.1:2
B.1:3
C.1:4
D.1:6
6.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
7.梯形ABCD中,AD∥BC,AD=a,BC=b,EF∥AD交AB,CD于E,F,且梯形AEFD与梯形EBCF相似,则EF等于( )
A.
B.
C.
D.不能确定
8.如图,AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3等于( )
A.45°
B.60°
C.75°
D.90°
9.已知甲、乙两地图的比例尺分别为1:5000和1:20
000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2
B.2:5
C.1:4
D.4:1
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,那么所得的图形与原图形相比( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
二.填空题
11.某一时刻,一根4米长的旗杆的影子长6米,同一时刻一座建筑物的影子长36米,则这座建筑物的高度为
米.
12.长方形地基,长75米,宽30米,把它画在比例尺是1:100的图纸上,长应是
cm,宽应是
cm.
13.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
14.如图,在△ABC中,DE∥BC,AD=1cm,BD=5cm,BC=6cm,则DE=
cm.
15.把边长为4cm的正方形作相似变换,放大到原来的5倍,放大后所得图形的周长为
cm,面积为
cm2.
16.同一底片印出来的不同尺寸的照片也是
.
17.如图所示,顶角A为36°的第一个黄金三角形△ABC的腰AB=1,底边与腰之比为K,三角形△BCD为第二个黄金三角形,依此类推,第2008个黄金三角形的周长为
.
18.如图,三个全等的正六边形,其中成位似图形关系的有
对.
19.两个相似三角形的周长分别为5cm和16cm,则它们对应边上的高之比为
.
20.如图所示,AD是△ABC的中线,F是AD上一点,CF的延长线交AB于点E,若AF:FD=1:3,则AE:AB=
.
三.解答题
21.已知一矩形长20cm,宽为10cm,另一与它相似的矩形的一边长为10cm,求另一边长.
22.若=,求的值.
23.如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:
(1)用圆规在CA上截取CD=CB,保留痕迹,标注点D;再以点A为圆心,AD为半径画弧交AB于点P,保留痕迹,标注点P;
(2)证明点P是线段AB的黄金分割点.
24.如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
25.同学们都知道,在相同的时刻,物高与影长成比例.某班同学要测量学校旗杆的高度,在某一时刻,量得旗杆的影长是8m,而同一时刻,量得某一身高为1.5m的同学的影长为1
m,求旗杆的高度.
26.如图,∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?
27.如图,△ABC的顶点分别为(1,1)、(4,1)、(2.5,3),将△ABC作下列变换,画出相应的图形并写出变换后三个顶点的坐标.
(1)关于y轴对称;
(2)沿y轴向下平移3个单位;
(3)以点O为位似中心,放大1倍.
参考答案与试题解析
一.选择题
1.解:∵ad=bc,
∴写成比例式为:a:b=c:d、b:d=a:c、b:a=d:c,
故选:D.
2.解:A、只有一个角为30°的等腰三角形,30°的角必定是顶角,所以,底角也一定相等,三角形相似,故本选项正确;
B、邻边之比为2,夹角不一定相等,两平行四边形不一定相似,故本选项错误;
C、底角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误;
D、有一个角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误.
故选:A.
3.解:∵两个相似三角形的相似比是,
∴S大三角形:S小三角形=()2=,
又∵S小三角形=14,
∴S大三角形=Cm2.
故选:D.
4.解:A、中三个角对应相等,所以两个三角形相似;
B、中对应边不成比例,所以不能判定其相似,B不正确;
C、∵AB=1,AC=1.5,BC=2,DE=12,EF=24,DF=18,
∴,即==,
故即对应边成比例,C对;
D、中两边与一角,求是两边的夹角,所以D对.
故选:B.
5.解:设斜边AB上的高为CD,垂足为D,
∴sinA=,
∴AB==,
∵cos∠DCB=cos15°=,
∴CD=cos15?BC,
∴==,
故选:C.
6.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
7.解:梯形AEFD与梯形EBCF相似,
则对应边的比相等,
因而得到:AD:EF=EF:BC
即a:EF=EF:b,
则EF2=ab
∴EF=.
故选:A.
8.解:∵AB=BC,∠B=90°,∴∠1=45°.
设AB=BC=CD=DE=1,则AC=,CE=2,
∴,
∴△ACE∽△DCA,∴∠2=∠CAE.
∵∠1=∠CAE+∠3=∠2+∠3,
∴∠1+∠2+∠3=90°.
故选:D.
9.解:把图上距离看作单位1,设A、B和C、D两地的实际距离分别为x和y,则:
1:5000=1:x,
解得x=5000,
1:20000=1:y,
解得y=20000,
∴x:y=5000:20000=1:4.
故选:C.
10.解:∵一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,
∴整个图形被纵向压缩为原来的一半
故选:D.
二.填空题
11.解:设建筑物高为x,根据在同一时刻同一地点任何物体的高与其影子长的比值相同得,
∴x=24,
∴建筑物的高为24米,
故答案为:24.
12.解:根据图上距离=实际距离×比例尺,
得图上长应是75×=0.75m=75cm,
宽应是30×=0.3m=30cm.
13.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
14.解:如图,∵AD=1cm,BD=5cm,
∴AB=AD+BD=6cm.
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
则ED=1cm.
故答案是:1.
15.解:放大5倍,即边长变为20,
所以周长为20×4=80cm;
面积为20×20=400cm2
16.解:同一底片印出来的不同尺寸的照片,形状相同,但大小不同,∴是相似图形.
17.解:第一个三角形的周长为K+2;
第二个三角形的周长K+K+K2=K(K+2);
第三个周长为K2+K2+K3=K2(K+2)
…
所以第2008个三角形的周长为K2007(K+2)
18.解:成位似图形关系的有3对.
19.解:已知两个相似三角形的周长分别为5cm和16cm,
则它们的相似比是5:16,
那么它们对应边上的高之比为5:16.
故答案为:5:16.
20.解:∵AF:FD=1:3
∴
作DG∥CE,交AB于点G
∵D是BC的中点
∴EC=2DG
∴
∴EF=DG
∴
∴AG=4AE
∴EG=BG=3AE
∴AB=7AE
∴AE:AB=1:7.
三.解答题
21.解:设另一边是xcm.
当所求的边与20cm的边是对应边时,根据题意得:20:10=x:10
解得:x=20cm;
当所求的边与10cm的边是对应边时,根据题意得20:10=10:x
解得:x=5cm;
因而另一边长长是20cm或5cm.
22.解:∵=,
∴8x﹣6y=x﹣y,
x=,
∴==.
23.解:(1)如图所示:
(2)设BC=x,则AB=2x,AC=x,
由题意得,CD=x,
则AP=AD=(﹣1)x,
=,
则点P是线段AB的黄金分割点.
24.解:(1)过D作DE∥AC,交BF于点E,
∴∠PDE=∠PAF,
∵P是AD的中点,
∴AP=DP,
∵在△PDE和△PAF中,
,
∴△PDE≌△PAF(ASA),
∴PE=PF,
由DE∥AC,得到=,
∵AD是△ABC的中线,
∴BD=DC,
∴BE=EF=2PF,
∴BP=3PF;
(2)∵△PDE≌△PAF,
∴DE=AF,
∴==,
∴AF=AC=×12=4.
25.解:∵物高与影长成比例,
∴旗杆的高度:8=1.5:1,
∴旗杆的高度=1.5×8=12米.
答:旗杆的高度是12米.
26.解:若△ABC∽△CDB,则有=,
即=,∴BD=,
当BD=时,△ABC∽△CDB.
27.解:
(1)A1(﹣1,1)、B1(﹣4,1)、C1、(2.5,3);
(2)A2(1,﹣2)、B2(4,﹣2)、C2(2.5,0);
(3)A3(2,2)、B3(8,2)、C3(5,6).
