中考专题复习——规律探索型问题
图片预览

文档简介
中考专题复习
——规律探索型问题
教学目标:
知识与技能:会用代数式表示问题中的数量关系,并验证所探索的规律。
过程与方法:经历探索数量关系,运用符号表示规律,通过运算验证规律的过程,培养学生观察比较、推理归纳、猜想验证的能力
情感态度与价值观:培养学生不怕困难、勇于探索的学习态度,合作交流的意识和能力,感受符号运算的作用.
重点:利用代数式表示规律
难点:探索规律的方法
关键:鼓励学生在探索规律的过程中从多角度进行考虑,用语言、表格、符号多种形式表示规律
教学过程:
热身运动
1、有一串单项式:a,2a2,3a3,4a4,…,19a19,20a20,…那么第n个单项式是 。
2、下列给出的一串数:1,3,5,7,9,……那么第n个数是 ;那么第50个数是 ;
1+3=4=22 ; 1+3+5=9=32 ; 1+3+5+7=16=42 ; ……1+3+5+7+ 9+ … … +99 = ____ ;
猜想:前n个奇数和
1+3+5+7+ 9+ … … + (2n-1) = ____
3、在公式(a+1)2=a2+2a+1中,当a分别取 1,2,3,…,n时,可得下列几个等式:
(1+1)2=12+2×1+1;(2+1)2=22+2×2+1;(3+1)2=32+2×3+1 …(n+1)2=n2+2×n+1
将这n个等式的左、右两边分别相加,可推出前n个自然数和
1+2+3+4+······+n=
再将这个等式的两边同时乘以2,可推出前n个偶数和:
2+4+6+8+······+2n=
4、下图是某同学在沙滩上用石子摆成的小房子.
观察图形的变化规律,写出第n个小房子用了_________块石子
归纳小结:
规律探索型问题即根据题目的条件(包括有规律算式、图表、图形等信息),从简单或特殊情况入手,进行归纳,并大胆猜想探索,得出结论,再通过具体验证而获得规律。
思考:解决规律探究问题的方法步骤?
三、经典例题
例1:一张白纸引发的规律:将一张长方形的纸对折,可得到两层。继续对折,对折时每次折痕与上次的折痕保持平行
1、连续对折3次后,可以得到几层
对折次数 1 2 3 4 … n
所得层数
2、若这张纸的厚度是0.1毫米,将它对折一次后,厚度为2×0.1毫米,对折3次后厚度为多少毫米 每层楼平均高3米,这张纸对折20次后有多少层楼高?
3、连续对折3次后,可以得到几条折痕
对折次数 1 2 3 4 … n
折痕条数
4、若这张白纸的面积为1,连续对折3次后单层面积是多少?
对折次数 1 2 3 4 … n
面积
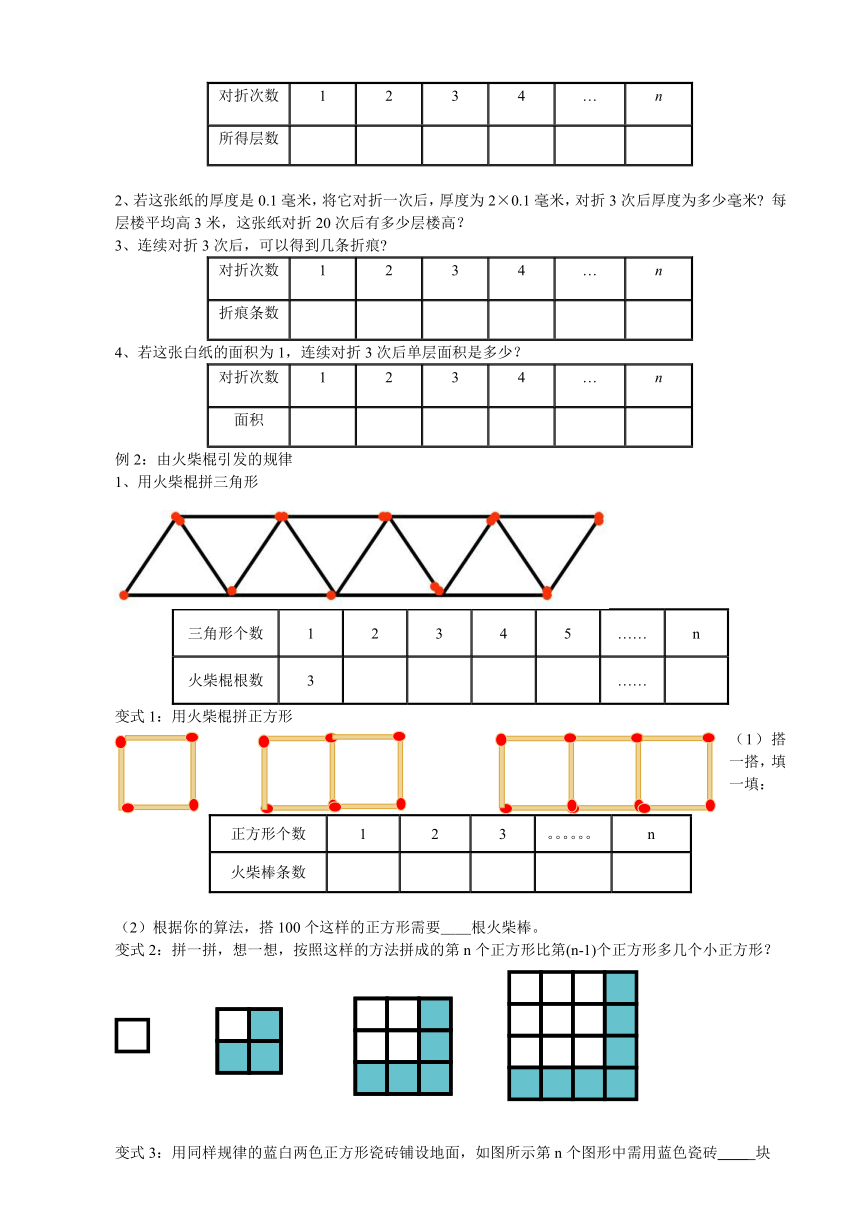
例2:由火柴棍引发的规律
1、用火柴棍拼三角形
三角形个数 1 2 3 4 5 …… n
火柴棍根数 3 ……
变式1:用火柴棍拼正方形
(1)搭一搭,填一填:
正方形个数 1 2 3 。。。。。。 n
火柴棒条数
(2)根据你的算法,搭100个这样的正方形需要__根火柴棒。
变式2:拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个小正方形?
变式3:用同样规律的蓝白两色正方形瓷砖铺设地面,如图所示第n个图形中需用蓝色瓷砖__ 块
四、归纳总结
1、探索规律的步骤和方法:形中找数,定规律;图形拼接,拆部分;图形运动,定周期
2、对于与自然数n有关的探索规律的题,可从已知条件入手,寻找所得“结果数”与n(个、次)的变化关系式 。(n的一次式或二次式)
五、深化巩固及作业
1、 搭1条、2条、3条如图所示的小鱼各用几根火柴棒?搭20条这样的小鱼用几根火柴?搭n条这样的小鱼呢?
2、如图拼接瓷砖,如果用了n块灰色瓷砖,需要多少块白瓷砖
3、下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用____和____枚棋子
(2)第n个“上”字需用________枚棋子
4、右边是一个有规律排列的数表,请用含n的代数式(n为正整数)表示数表中第n行第n列的数:_____________
第一列 第二列 第三列 第四列 …
第一行 1 2 5 10
第二行 4 3 6 11
第三行 9 8 7 12
第四行 16 15 14 13
…
5、如图5,已知四边形ABCD是梯形(标注的数字为边长),按图中所示的规律,用n个这样的梯形镶嵌而成的四边形的周长是___________.
6、如图,将边长为1的正△OAP沿着x轴正方向连续翻转2010次, 点P依次落在点P1,P2,P3 ,…,P2010的位置,则点P2010的横坐标是 。
7、如图,是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,则摆出的正方形所用的火柴棍的根数为
8、下面是按照一定规律画出的一列“树型”图:
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.
9、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个
10、如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,……,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=________
六、请同学们谈谈上了这节课后的感想……
七、课外拓展
假如我校食堂餐厅要安排40人同时就餐,请设计一种桌椅摆放方案,使没有剩余桌椅(要求选用下列图中的一种方式或两种混合摆放方式)。请说出你的设计方案。
……
……
——规律探索型问题
教学目标:
知识与技能:会用代数式表示问题中的数量关系,并验证所探索的规律。
过程与方法:经历探索数量关系,运用符号表示规律,通过运算验证规律的过程,培养学生观察比较、推理归纳、猜想验证的能力
情感态度与价值观:培养学生不怕困难、勇于探索的学习态度,合作交流的意识和能力,感受符号运算的作用.
重点:利用代数式表示规律
难点:探索规律的方法
关键:鼓励学生在探索规律的过程中从多角度进行考虑,用语言、表格、符号多种形式表示规律
教学过程:
热身运动
1、有一串单项式:a,2a2,3a3,4a4,…,19a19,20a20,…那么第n个单项式是 。
2、下列给出的一串数:1,3,5,7,9,……那么第n个数是 ;那么第50个数是 ;
1+3=4=22 ; 1+3+5=9=32 ; 1+3+5+7=16=42 ; ……1+3+5+7+ 9+ … … +99 = ____ ;
猜想:前n个奇数和
1+3+5+7+ 9+ … … + (2n-1) = ____
3、在公式(a+1)2=a2+2a+1中,当a分别取 1,2,3,…,n时,可得下列几个等式:
(1+1)2=12+2×1+1;(2+1)2=22+2×2+1;(3+1)2=32+2×3+1 …(n+1)2=n2+2×n+1
将这n个等式的左、右两边分别相加,可推出前n个自然数和
1+2+3+4+······+n=
再将这个等式的两边同时乘以2,可推出前n个偶数和:
2+4+6+8+······+2n=
4、下图是某同学在沙滩上用石子摆成的小房子.
观察图形的变化规律,写出第n个小房子用了_________块石子
归纳小结:
规律探索型问题即根据题目的条件(包括有规律算式、图表、图形等信息),从简单或特殊情况入手,进行归纳,并大胆猜想探索,得出结论,再通过具体验证而获得规律。
思考:解决规律探究问题的方法步骤?
三、经典例题
例1:一张白纸引发的规律:将一张长方形的纸对折,可得到两层。继续对折,对折时每次折痕与上次的折痕保持平行
1、连续对折3次后,可以得到几层
对折次数 1 2 3 4 … n
所得层数
2、若这张纸的厚度是0.1毫米,将它对折一次后,厚度为2×0.1毫米,对折3次后厚度为多少毫米 每层楼平均高3米,这张纸对折20次后有多少层楼高?
3、连续对折3次后,可以得到几条折痕
对折次数 1 2 3 4 … n
折痕条数
4、若这张白纸的面积为1,连续对折3次后单层面积是多少?
对折次数 1 2 3 4 … n
面积
例2:由火柴棍引发的规律
1、用火柴棍拼三角形
三角形个数 1 2 3 4 5 …… n
火柴棍根数 3 ……
变式1:用火柴棍拼正方形
(1)搭一搭,填一填:
正方形个数 1 2 3 。。。。。。 n
火柴棒条数
(2)根据你的算法,搭100个这样的正方形需要__根火柴棒。
变式2:拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个小正方形?
变式3:用同样规律的蓝白两色正方形瓷砖铺设地面,如图所示第n个图形中需用蓝色瓷砖__ 块
四、归纳总结
1、探索规律的步骤和方法:形中找数,定规律;图形拼接,拆部分;图形运动,定周期
2、对于与自然数n有关的探索规律的题,可从已知条件入手,寻找所得“结果数”与n(个、次)的变化关系式 。(n的一次式或二次式)
五、深化巩固及作业
1、 搭1条、2条、3条如图所示的小鱼各用几根火柴棒?搭20条这样的小鱼用几根火柴?搭n条这样的小鱼呢?
2、如图拼接瓷砖,如果用了n块灰色瓷砖,需要多少块白瓷砖
3、下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用____和____枚棋子
(2)第n个“上”字需用________枚棋子
4、右边是一个有规律排列的数表,请用含n的代数式(n为正整数)表示数表中第n行第n列的数:_____________
第一列 第二列 第三列 第四列 …
第一行 1 2 5 10
第二行 4 3 6 11
第三行 9 8 7 12
第四行 16 15 14 13
…
5、如图5,已知四边形ABCD是梯形(标注的数字为边长),按图中所示的规律,用n个这样的梯形镶嵌而成的四边形的周长是___________.
6、如图,将边长为1的正△OAP沿着x轴正方向连续翻转2010次, 点P依次落在点P1,P2,P3 ,…,P2010的位置,则点P2010的横坐标是 。
7、如图,是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n根火柴棍时,则摆出的正方形所用的火柴棍的根数为
8、下面是按照一定规律画出的一列“树型”图:
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.
9、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个
10、如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,……,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=________
六、请同学们谈谈上了这节课后的感想……
七、课外拓展
假如我校食堂餐厅要安排40人同时就餐,请设计一种桌椅摆放方案,使没有剩余桌椅(要求选用下列图中的一种方式或两种混合摆放方式)。请说出你的设计方案。
……
……
同课章节目录
