2020-2021学年七年级数学人教版下册课件 8.3实际问题与二元一次方程组(3)(15张)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册课件 8.3实际问题与二元一次方程组(3)(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 157.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 23:44:53 | ||
图片预览



文档简介
8.3 实际问题与二元一次方程组(3)
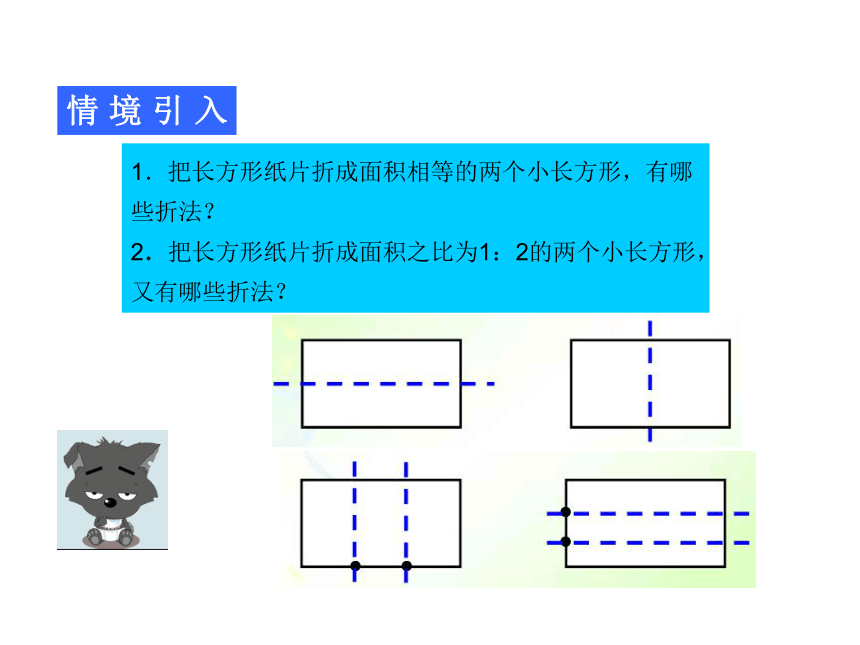
情境引入
1.把长方形纸片折成面积相等的两个小长方形,有哪些折法?
2.把长方形纸片折成面积之比为1:2的两个小长方形, 又有哪些折法?
尝试应用
1.木工厂有28个工人,每个工人一天加工桌子数与加工椅子数的比是9:20,现在如何安排劳动力,使生产的一张桌子与4只椅子配套?
解:设安排x名工人加工桌子,y名工人加工椅子.
找出相等关系列方程组得
解这个方程组,得
答:安排10名工人加工桌子,18名工人加工椅子.
尝试应用
2.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽.
解:设原长方形的长为x,原长方形的宽为y.
根据题意得
解这个方程组,得
答:原长方形的长为8cm,原长方形的宽为2cm.
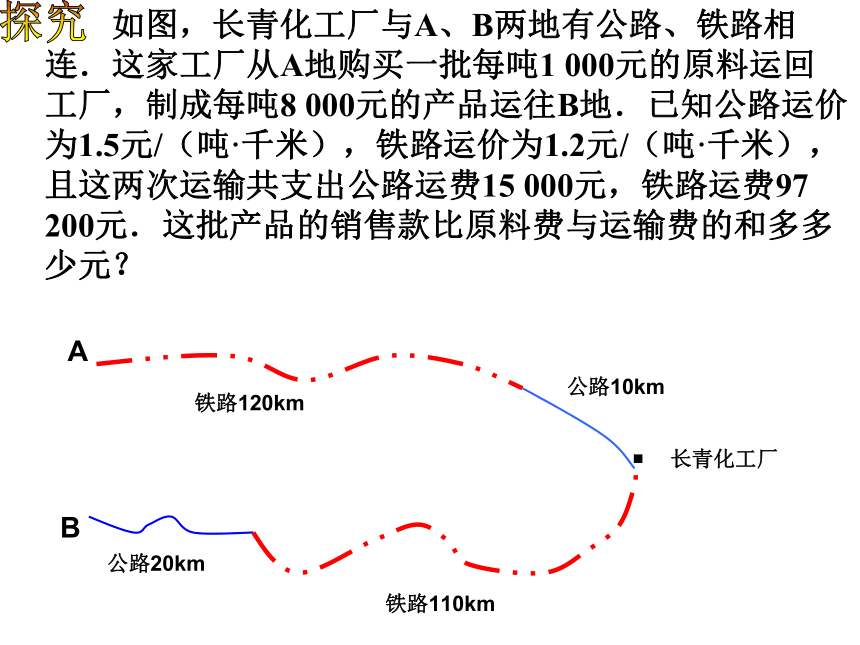
如图,长青化工厂与A、B两地有公路、铁路相
连.这家工厂从A地购买一批每吨1 000元的原料运回
工厂,制成每吨8 000元的产品运往B地.已知公路运价
为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
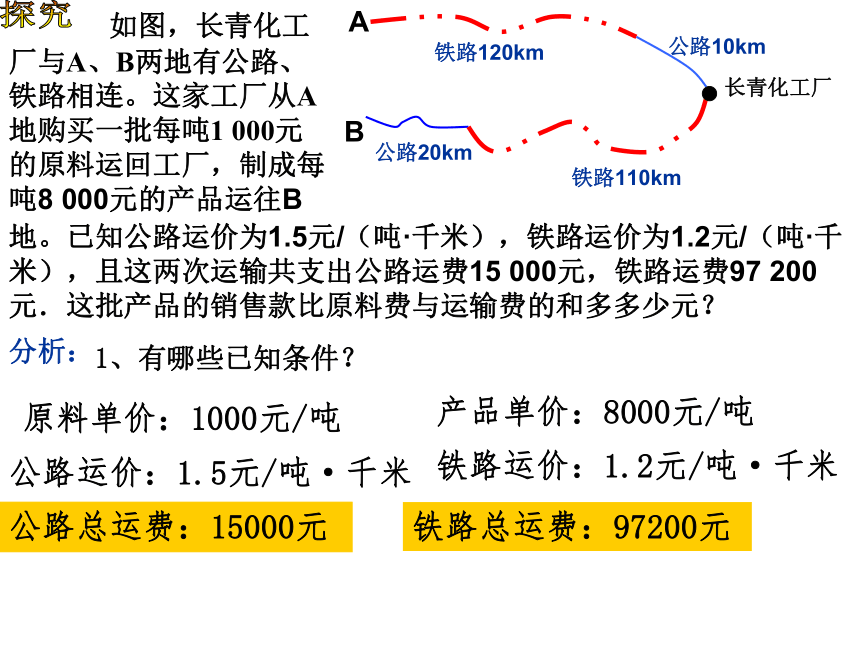
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
1、有哪些已知条件?
原料单价:1000元/吨
产品单价:8000元/吨
公路运价:1.5元/吨·千米
铁路运价:1.2元/吨·千米
公路总运费:15000元
铁路总运费:97200元
公路总运费:15000元
铁路总运费:97200元
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
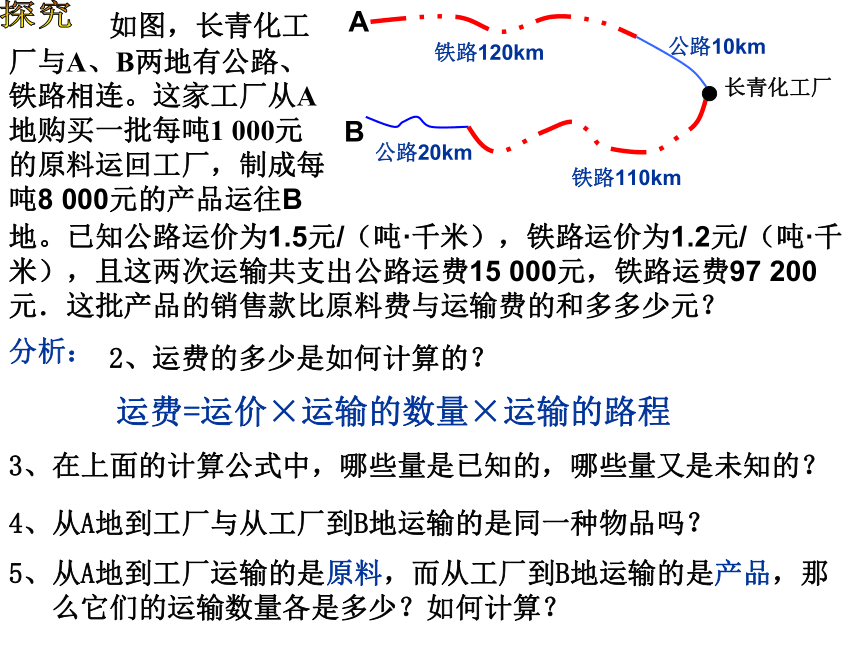
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
2、运费的多少是如何计算的?
运费=运价×运输的数量×运输的路程
3、在上面的计算公式中,哪些量是已知的,哪些量又是未知的?
4、从A地到工厂与从工厂到B地运输的是同一种物品吗?
5、从A地到工厂运输的是原料,而从工厂到B地运输的是产品,那
么它们的运输数量各是多少?如何计算?
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
运费=运价×运输的数量×运输的路程
5、从A地到工厂运输的是原料,而从工厂到B地运输的是产品,那
么它们的运输数量各是多少?如何计算?
6、所求的问题中的销售款大小除了与销售单价有关之外,还与什么量有关?原料费的大小又与哪些量有关呢?
销售款=产品数量×产品单价
原料款=原料数量×原料单价
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
运费=运价×运输的数量×运输的路程
销售款=产品数量×产品单价
原料款=原料数量×原料单价
通过以上分析可以发现,要解决问题,关键是求出原料的数量和产品的数量。如何求出这两个量?
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
设产品重x吨,原料重y吨,运费如何表示?
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
由上表,可列出方程组
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
解:
铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
设产品重x吨,原料重y吨,根据题意可列得方程组
化简,得
解得
所以销售款为
原料费为
=2400000(元)
=400000(元)
8000×300
1000×400
答:这批产品的销售款比原料费与运输费的和多188.78万元。
巩固训练
1、为引导公民节约用水,合理利用资源,各地采用价格调控等手段,某地规定如下用水收费标准,每月的用水不超过10吨,每吨按a元收费,超过10吨,超过的部分每吨按b元收费,小颖家7-8月份的用水记录如下:
月份
用水量(吨)
水费(元)
7
12
15
8
16
21
根据以上信息,你能求出a,b的值吗?
2.从甲地到乙地,先下山然后走平路。某人骑自行车从甲地以每小时12km的速度下山,而以每小时9km的速度通过平路,到乙地用了55min;他回来时以每小时8km的速度通过平路,而以每小时4km的速度上山,回到甲地用了3/2h。求甲乙两地的距离。
设:从甲地到乙地下坡为xkm,平路为ykm。
当堂达标
1.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
A. B.
C. D.
2.一张试卷有25道选择题,做对一题得4分,做错一题或不做扣1分.小英做了全部试题得70分,则她做对了________道题.
3.现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,用多少张铁皮做盒身,多少张铁皮做盒底可以使盒身与盒底正好配套?
“用二元一次方程组分析和解决实际问题”的基本过程
情境引入
1.把长方形纸片折成面积相等的两个小长方形,有哪些折法?
2.把长方形纸片折成面积之比为1:2的两个小长方形, 又有哪些折法?
尝试应用
1.木工厂有28个工人,每个工人一天加工桌子数与加工椅子数的比是9:20,现在如何安排劳动力,使生产的一张桌子与4只椅子配套?
解:设安排x名工人加工桌子,y名工人加工椅子.
找出相等关系列方程组得
解这个方程组,得
答:安排10名工人加工桌子,18名工人加工椅子.
尝试应用
2.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽.
解:设原长方形的长为x,原长方形的宽为y.
根据题意得
解这个方程组,得
答:原长方形的长为8cm,原长方形的宽为2cm.
如图,长青化工厂与A、B两地有公路、铁路相
连.这家工厂从A地购买一批每吨1 000元的原料运回
工厂,制成每吨8 000元的产品运往B地.已知公路运价
为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
1、有哪些已知条件?
原料单价:1000元/吨
产品单价:8000元/吨
公路运价:1.5元/吨·千米
铁路运价:1.2元/吨·千米
公路总运费:15000元
铁路总运费:97200元
公路总运费:15000元
铁路总运费:97200元
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
2、运费的多少是如何计算的?
运费=运价×运输的数量×运输的路程
3、在上面的计算公式中,哪些量是已知的,哪些量又是未知的?
4、从A地到工厂与从工厂到B地运输的是同一种物品吗?
5、从A地到工厂运输的是原料,而从工厂到B地运输的是产品,那
么它们的运输数量各是多少?如何计算?
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
运费=运价×运输的数量×运输的路程
5、从A地到工厂运输的是原料,而从工厂到B地运输的是产品,那
么它们的运输数量各是多少?如何计算?
6、所求的问题中的销售款大小除了与销售单价有关之外,还与什么量有关?原料费的大小又与哪些量有关呢?
销售款=产品数量×产品单价
原料款=原料数量×原料单价
如图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
地。已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
运费=运价×运输的数量×运输的路程
销售款=产品数量×产品单价
原料款=原料数量×原料单价
通过以上分析可以发现,要解决问题,关键是求出原料的数量和产品的数量。如何求出这两个量?
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
分析:
铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
设产品重x吨,原料重y吨,运费如何表示?
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
由上表,可列出方程组
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运往B地.公路运价为1.5元/(吨·千米),
探究
A
B
铁路120km
公路10km
长青化工厂
铁路110km
公路20km
解:
铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
设产品重x吨,原料重y吨,根据题意可列得方程组
化简,得
解得
所以销售款为
原料费为
=2400000(元)
=400000(元)
8000×300
1000×400
答:这批产品的销售款比原料费与运输费的和多188.78万元。
巩固训练
1、为引导公民节约用水,合理利用资源,各地采用价格调控等手段,某地规定如下用水收费标准,每月的用水不超过10吨,每吨按a元收费,超过10吨,超过的部分每吨按b元收费,小颖家7-8月份的用水记录如下:
月份
用水量(吨)
水费(元)
7
12
15
8
16
21
根据以上信息,你能求出a,b的值吗?
2.从甲地到乙地,先下山然后走平路。某人骑自行车从甲地以每小时12km的速度下山,而以每小时9km的速度通过平路,到乙地用了55min;他回来时以每小时8km的速度通过平路,而以每小时4km的速度上山,回到甲地用了3/2h。求甲乙两地的距离。
设:从甲地到乙地下坡为xkm,平路为ykm。
当堂达标
1.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
A. B.
C. D.
2.一张试卷有25道选择题,做对一题得4分,做错一题或不做扣1分.小英做了全部试题得70分,则她做对了________道题.
3.现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,用多少张铁皮做盒身,多少张铁皮做盒底可以使盒身与盒底正好配套?
“用二元一次方程组分析和解决实际问题”的基本过程
