2020-2021学年人教版七年级数学下册6.3实数课件(共49张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册6.3实数课件(共49张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 10:18:53 | ||
图片预览






文档简介
6.3实数(1)
(1)5的平方根是
(2) 的算术平方根是
(3)什么叫有理数?
回顾:
有理数是整数和分数的统称,一切有理数都可以化成分数的形式。
复习
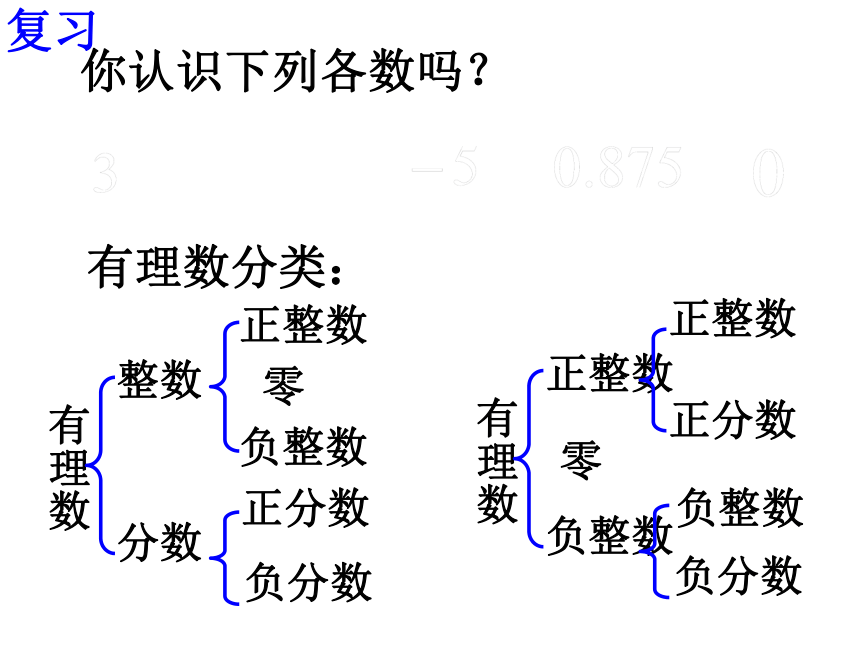
你认识下列各数吗?
有理数分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正整数
负整数
正整数
零
负整数
正分数
负分数
引入
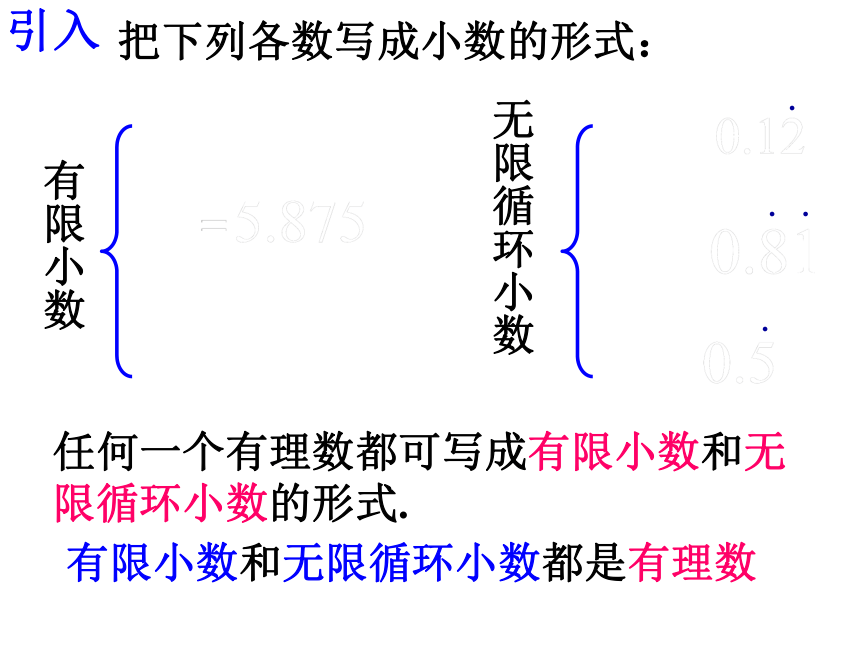
把下列各数写成小数的形式:
有限小数
无限循环小数
有限小数和无限循环小数都是有理数
任何一个有理数都可写成有限小数和无限循环小数的形式.
.
.
.
.
探究
把下列各数写成小数的形式:
无限不循环小数
无限不循环小数叫无理数
有理数和无理数统称为实数
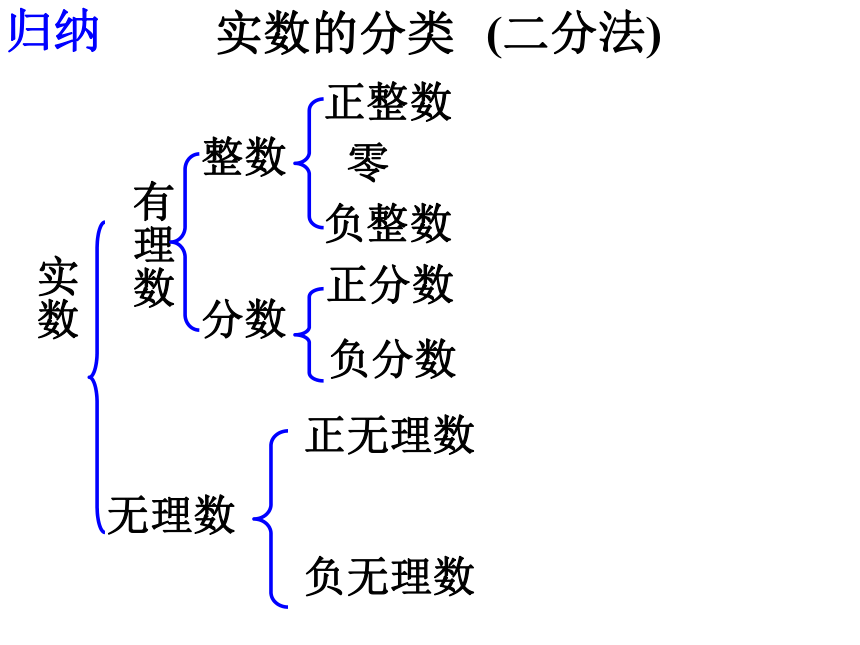
归纳
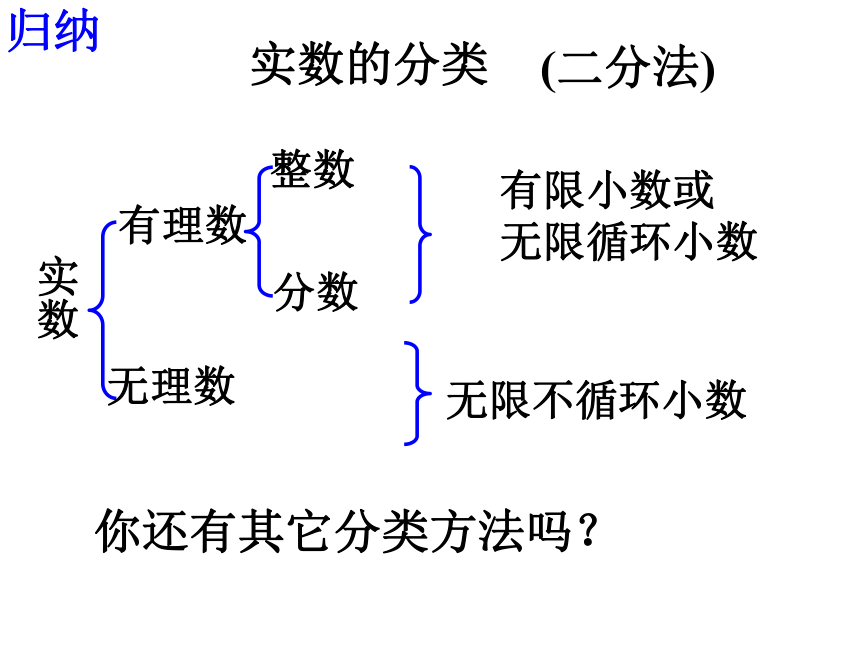
实数的分类
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
你还有其它分类方法吗?
(二分法)
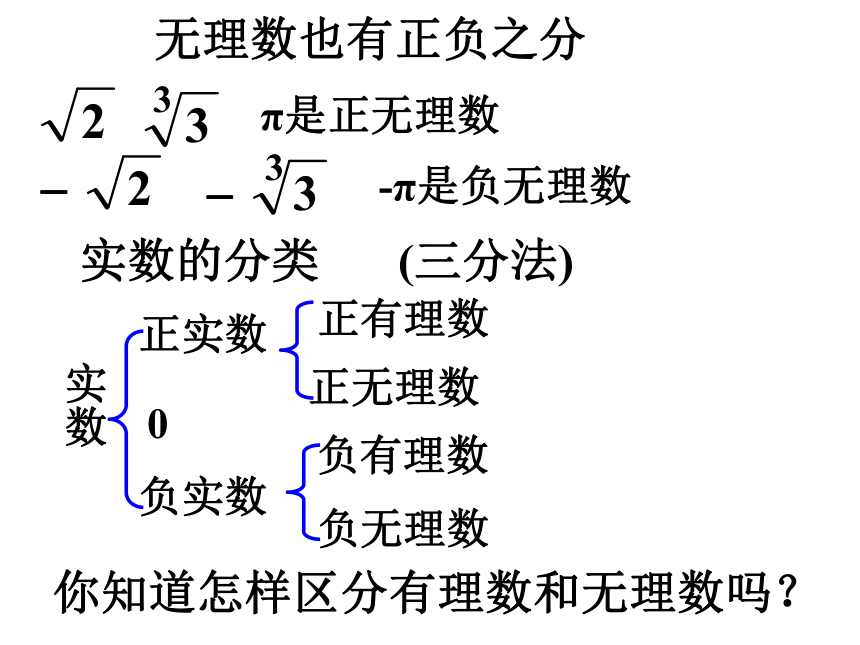
实数
正实数
负实数
正有理数
正无理数
你知道怎样区分有理数和无理数吗?
0
负无理数
负有理数
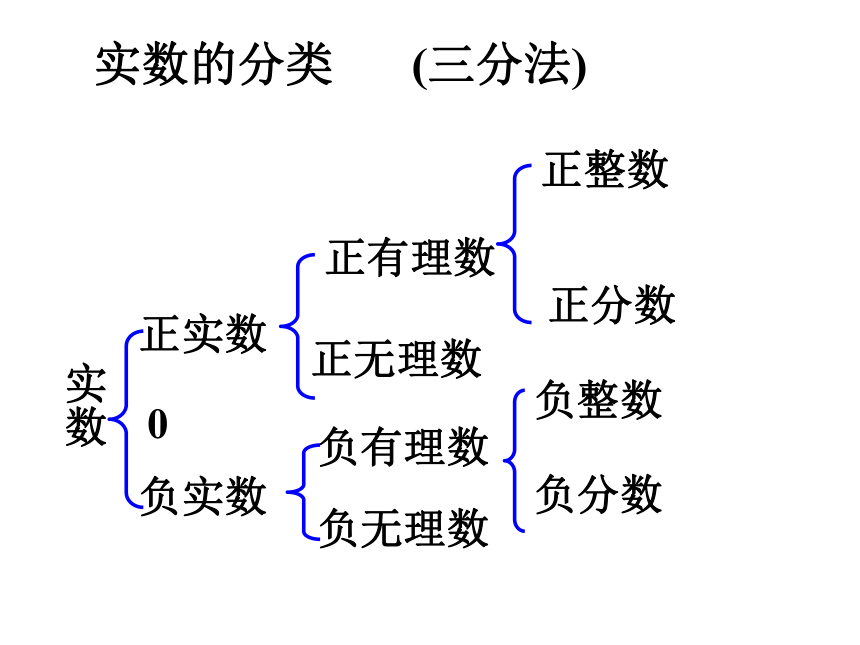
实数的分类
(三分法)
无理数也有正负之分
3
π是正无理数
3
-π是负无理数
归纳
实数的分类
实数
无理数
(二分法)
有理数
整数
分数
正整数
零
负整数
正分数
负分数
正无理数
负无理数
实数
正实数
负实数
正有理数
正无理数
0
负无理数
负有理数
实数的分类
(三分法)
正整数
负整数
正分数
负分数
例1、下列各数中,哪些是有理数,哪
些是无理数?
1.圆周率
2.开不尽的方根
3.人为构造的数
常见的无理数有以下三类:
.
1.探究新知
有理数包括整数和分数,如果将下列分数写成小数的形式,你有什么发现?
.
..
是不是有理数?
是不是整数?
是不是分数?
结论: 既不是整数,也不是分数。
所以, 不是有理数。
议一议
我们把这种无限不循环小数叫做无理数。
圆周率 及一些含有 的数都是无理数
例如:
2)像 的数是无理数。
1)
3) 有一定的规律,但不循环的无限小数都是无理数。
例如:
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
想一想:凡是带有根号的数都是无理数吗?
不一定
实数的分类
有理数和无理数统称实数.
1.圆周率 及一些含有 的数
2.开不尽方的数
3.无限不循环小数
无理数的特征:
判断下列数哪些是有理数?哪些是无理数?
有理数是:
无理数是:
, ,
, ,
练习:
归纳
实数的分类
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
你还有其它分类方法吗?
(定义)
1.探究新知
因为非零有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗?
归纳
实数的分类
实数
正实数
负实数
正有理数
正无理数
你知道怎样区分有理数和无理数吗?
0
负无理数
负有理数
(正负)
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
练一练
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)实数集合:
在数轴上表示下列各数:
-3 -2 -1 0 1 2 3 4
有理数都可以用数轴上的点表示
探究
直径为1个单位长度的圆从原点沿
数轴向右滚动一周,圆上的一点由原点
到达O′,点O′的坐标是多少?
0 1 2 3 4
O′
探究
0 1 2 3 4
你有什么发现?
无理数π可以用数轴上的点表示
O′
再探
以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?
-2 -1 0 1 2
无理数 可以用数轴上的点表示
归纳
0 1 2 3 4
1、每一个有理数都可以用数轴上的点
表示;
2、每一个无理数都可以用数轴上的点
表示;
实数与数轴上的点是一一对应的
每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.
数轴上一个点
有一个实数
点 数
有一个实数
数轴上一个点
数 点
即实数和数轴上点是一一对应的.
随堂练习
判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
2.运用新知
判断正误,并说明理由.
(1)无理数都是无限小数;
(2) 实数包括正实数、0、负实数;
(3)不带根号的数都是有理数;
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.
×
×
6.3实数(2)
探究
的相反数是 ;
的相反数是 ;
的相反数是 ;
-2 -1 0 1 2
a的相反数是-a
探究
-2 -1 0 1 2
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
想一想
a是一个实数,它的相反数为 -a
0的相反数是_______
的相反数是_______
的相反数是_______
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0
想一想
(1)a是一个实数,它的相反数为 ,
绝对值为 ;
(2)如果a 0,那么它的倒数为 。
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
( 3 ) 正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
结合有理数相反数和绝对值的意义,
你能说说实数关于相反数和绝对值的意义吗?
2.探究新知
1.数 的相反数是 ,
2.一个正实数的绝对
值是它本身;
一个负实数的绝对
值是它的相反数;
0的绝对值是0.
例1
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
3.运用新知
解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是4.
(4) 绝对值是 的数是 或 .
3 .运用新知
3、实数的运算:
实数之间可以进行加、减、乘、除(除数不为0)、乘方、非负实数的开方运算,还有任意实数的开立方运算,在进行实数的运算中,交换律、结合律、分配律等运算性质也适用。
3.运用新知
例2 计算下列各式的值:
(1)
(2)
3.运用新知
例3 计算(结果保留小数点后两位):
;
解:
3.运用新知
练习1 求下列各数的相反数与绝对值:
练习2 计算 :
3.运用新知
练习3 计算
练习2、填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________
的平方 是___ .
(6) 比较大小:-7
填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
练习:
5、绝对值等于 的数是 。
实力神枪手——看谁百发百中
填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
3、一个数的绝对值是 ,则这个数是 .
合作学习
请同学们总结有理数的运算律和运算法则
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
实数的运算顺序
先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算
例3:计算
( 1 ) (精确到0.01);
( 2 ) (结果保留3个有效数字)
在实数运算中,当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算。
在中间运算中 ,为了使结果更精确,精确度要比预定的精确度多取一位
解:
(1)5的平方根是
(2) 的算术平方根是
(3)什么叫有理数?
回顾:
有理数是整数和分数的统称,一切有理数都可以化成分数的形式。
复习
你认识下列各数吗?
有理数分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正整数
负整数
正整数
零
负整数
正分数
负分数
引入
把下列各数写成小数的形式:
有限小数
无限循环小数
有限小数和无限循环小数都是有理数
任何一个有理数都可写成有限小数和无限循环小数的形式.
.
.
.
.
探究
把下列各数写成小数的形式:
无限不循环小数
无限不循环小数叫无理数
有理数和无理数统称为实数
归纳
实数的分类
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
你还有其它分类方法吗?
(二分法)
实数
正实数
负实数
正有理数
正无理数
你知道怎样区分有理数和无理数吗?
0
负无理数
负有理数
实数的分类
(三分法)
无理数也有正负之分
3
π是正无理数
3
-π是负无理数
归纳
实数的分类
实数
无理数
(二分法)
有理数
整数
分数
正整数
零
负整数
正分数
负分数
正无理数
负无理数
实数
正实数
负实数
正有理数
正无理数
0
负无理数
负有理数
实数的分类
(三分法)
正整数
负整数
正分数
负分数
例1、下列各数中,哪些是有理数,哪
些是无理数?
1.圆周率
2.开不尽的方根
3.人为构造的数
常见的无理数有以下三类:
.
1.探究新知
有理数包括整数和分数,如果将下列分数写成小数的形式,你有什么发现?
.
..
是不是有理数?
是不是整数?
是不是分数?
结论: 既不是整数,也不是分数。
所以, 不是有理数。
议一议
我们把这种无限不循环小数叫做无理数。
圆周率 及一些含有 的数都是无理数
例如:
2)像 的数是无理数。
1)
3) 有一定的规律,但不循环的无限小数都是无理数。
例如:
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
想一想:凡是带有根号的数都是无理数吗?
不一定
实数的分类
有理数和无理数统称实数.
1.圆周率 及一些含有 的数
2.开不尽方的数
3.无限不循环小数
无理数的特征:
判断下列数哪些是有理数?哪些是无理数?
有理数是:
无理数是:
, ,
, ,
练习:
归纳
实数的分类
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
你还有其它分类方法吗?
(定义)
1.探究新知
因为非零有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗?
归纳
实数的分类
实数
正实数
负实数
正有理数
正无理数
你知道怎样区分有理数和无理数吗?
0
负无理数
负有理数
(正负)
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
练一练
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)实数集合:
在数轴上表示下列各数:
-3 -2 -1 0 1 2 3 4
有理数都可以用数轴上的点表示
探究
直径为1个单位长度的圆从原点沿
数轴向右滚动一周,圆上的一点由原点
到达O′,点O′的坐标是多少?
0 1 2 3 4
O′
探究
0 1 2 3 4
你有什么发现?
无理数π可以用数轴上的点表示
O′
再探
以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?
-2 -1 0 1 2
无理数 可以用数轴上的点表示
归纳
0 1 2 3 4
1、每一个有理数都可以用数轴上的点
表示;
2、每一个无理数都可以用数轴上的点
表示;
实数与数轴上的点是一一对应的
每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.
数轴上一个点
有一个实数
点 数
有一个实数
数轴上一个点
数 点
即实数和数轴上点是一一对应的.
随堂练习
判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
2.运用新知
判断正误,并说明理由.
(1)无理数都是无限小数;
(2) 实数包括正实数、0、负实数;
(3)不带根号的数都是有理数;
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.
×
×
6.3实数(2)
探究
的相反数是 ;
的相反数是 ;
的相反数是 ;
-2 -1 0 1 2
a的相反数是-a
探究
-2 -1 0 1 2
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
想一想
a是一个实数,它的相反数为 -a
0的相反数是_______
的相反数是_______
的相反数是_______
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0
想一想
(1)a是一个实数,它的相反数为 ,
绝对值为 ;
(2)如果a 0,那么它的倒数为 。
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
( 3 ) 正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
结合有理数相反数和绝对值的意义,
你能说说实数关于相反数和绝对值的意义吗?
2.探究新知
1.数 的相反数是 ,
2.一个正实数的绝对
值是它本身;
一个负实数的绝对
值是它的相反数;
0的绝对值是0.
例1
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
3.运用新知
解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是4.
(4) 绝对值是 的数是 或 .
3 .运用新知
3、实数的运算:
实数之间可以进行加、减、乘、除(除数不为0)、乘方、非负实数的开方运算,还有任意实数的开立方运算,在进行实数的运算中,交换律、结合律、分配律等运算性质也适用。
3.运用新知
例2 计算下列各式的值:
(1)
(2)
3.运用新知
例3 计算(结果保留小数点后两位):
;
解:
3.运用新知
练习1 求下列各数的相反数与绝对值:
练习2 计算 :
3.运用新知
练习3 计算
练习2、填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是____,
(3)| |=___________
(4)绝对值等于 的数是 _________
的平方 是___ .
(6) 比较大小:-7
填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
练习:
5、绝对值等于 的数是 。
实力神枪手——看谁百发百中
填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
3、一个数的绝对值是 ,则这个数是 .
合作学习
请同学们总结有理数的运算律和运算法则
1.交换律 : 加法 a+b=b+a
乘法a×b=b×a
2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)
3.分配律: a× (b+c)= a×b+ a×c
注:有理数的运算律和运算法则在实数范围内同样适用
实数的运算顺序
先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算
例3:计算
( 1 ) (精确到0.01);
( 2 ) (结果保留3个有效数字)
在实数运算中,当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算。
在中间运算中 ,为了使结果更精确,精确度要比预定的精确度多取一位
解:
