2.1平面向量的实际背景及基本概念课件(苏教版必修4)
文档属性
| 名称 | 2.1平面向量的实际背景及基本概念课件(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-23 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
在物理和数学中,我们学习了很多“量”,如年龄,
身高,位移,长度,速度,加速度,面积,体积,力,
质量等,大家一起分析一下,这些“量”有什么不同?
* 数学中我们把年龄,身高,长度,面积,
体积,质量等叫数量;
*把位移,力,速度,加速度等叫向量。
数量只有大小,没有方向;
向量有大小,也有方向。
既有大小又有方向的量叫向量.
一. 向量的定义
向量通常用有向线段(带有方向的线段)来表示;
A(起点)
B(终点)
二.向量的表示
有向线段的三个要素:起点、方向、长度
a
以A为起点,B为终点的向量表示为:
或
注意:用a,b,c……表示向量时,
印刷用黑体a,书写用
此重点也,望记住
三.向量的有关概念
单位向量:长度为1个单位长度的向量。
2.两个基本向量:
1.向量的长度(模): 向量 的大小
表示为:
,
零向量:长度为零的向量(方向任意).
表示为:
0
|
0
|
=
0
3. 向量的关系:
规定:零向量与任一向量平行; 记作:
平行向量: 方向相同或相反的非零向量叫平行向量.
表示为:
相等向量: 长度相等且方向相同的向量.
表示为:
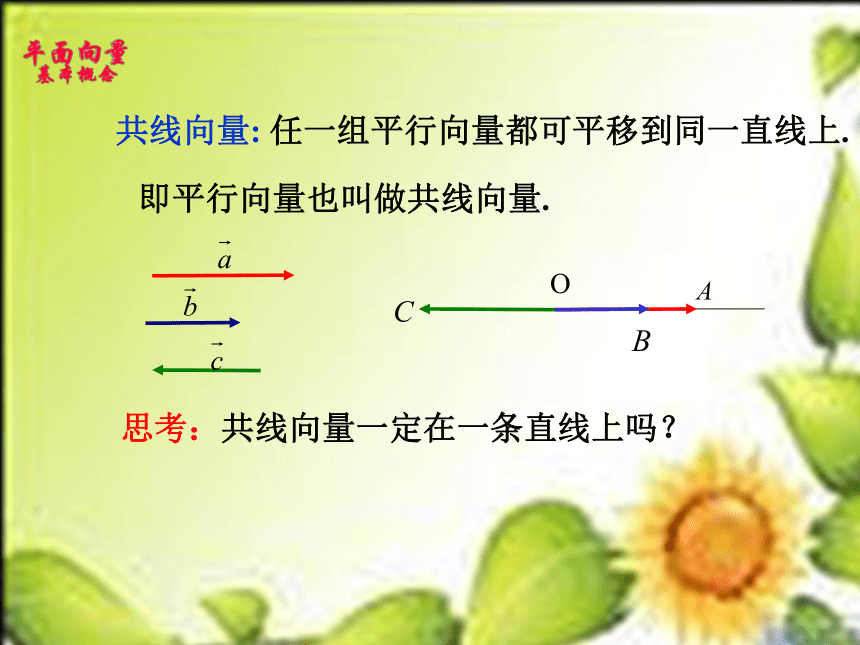
共线向量: 任一组平行向量都可平移到同一直线上.
即平行向量也叫做共线向量.
O
思考:共线向量一定在一条直线上吗?
巩固练习:判断下列结论是否正确。
(1)平行向量方向一定相同; ( )
(2)不相等向量一定不平行; ( )
(3)与零向量相等的向量是零向量; ( )
(4)与任何向量都平行的向量是零向量; ( )
(5)共线向量一定在一条直线上; ( )
(6)若两向量平行,则这两向量的方向相同或相反;
( )
(7)相等向量一定是平行向量。 ( )
×
×
√
√
×
×
√
O
例1.如图,设O是正六边形ABCDEF的中心,分别写
出图中与向量 相等的向量.
问题:
(1) 与 相等吗
(2) 与 相等吗
(3)与 长度相等的向量有几个
(4)与 共线的向量有哪几个
解:
相等的有7个
长度相等的有15个
根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(1)四边形ABCD是平行四边形。
(2)四边形ABCD是菱形。
四.课堂练习
1.判断下列结论是否正确,并说明理由。
(1)单位向量都是相等向量; ( )
(2)物理学中的作用力与反作用力是一对共线向量;( )
(3)方向为南偏西60°的向量与北偏东60°的向量是共线向
量; ( )
(4)直角坐标平面上的x轴、y轴都是向量。( )
×
√
√
×
2.已知边长为3的等边三角形ABC,求BC边上的中线向量
的模 。
向量的相反向量
定义:
※注意:
零向量的相反向量仍是零向量。
(1)下列各量中是向量的是( )
A.时间 B.速度
C.面积 D. 长度
练习:
(2)等腰梯形 中,对角线 与 相交于点 ,点 、
分别在两腰 、 上, 过点 且 ,则下列等式
正确的是( )
A. B.
C. D.
B
D
(3).下列说法正确的是 ( )
A) 方向相同或相反的向量是平行向量.
B) 零向量是 .
C)长度相等的向量叫做相等向量.
D) 共线向量是在一条直线上的向量.
B
(4).已知a、b是任意两个向量,下列条件:
①a=b; ②|a|=|b|; ③a与b的方向相反;
④a=0或b=0; ⑤ a与b都是单位向量.
能判定向量a与b平行的是_____.
①③④
小结:
提问:
1.本节主要介绍了哪些概念
2.向量如何表示
在物理和数学中,我们学习了很多“量”,如年龄,
身高,位移,长度,速度,加速度,面积,体积,力,
质量等,大家一起分析一下,这些“量”有什么不同?
* 数学中我们把年龄,身高,长度,面积,
体积,质量等叫数量;
*把位移,力,速度,加速度等叫向量。
数量只有大小,没有方向;
向量有大小,也有方向。
既有大小又有方向的量叫向量.
一. 向量的定义
向量通常用有向线段(带有方向的线段)来表示;
A(起点)
B(终点)
二.向量的表示
有向线段的三个要素:起点、方向、长度
a
以A为起点,B为终点的向量表示为:
或
注意:用a,b,c……表示向量时,
印刷用黑体a,书写用
此重点也,望记住
三.向量的有关概念
单位向量:长度为1个单位长度的向量。
2.两个基本向量:
1.向量的长度(模): 向量 的大小
表示为:
,
零向量:长度为零的向量(方向任意).
表示为:
0
|
0
|
=
0
3. 向量的关系:
规定:零向量与任一向量平行; 记作:
平行向量: 方向相同或相反的非零向量叫平行向量.
表示为:
相等向量: 长度相等且方向相同的向量.
表示为:
共线向量: 任一组平行向量都可平移到同一直线上.
即平行向量也叫做共线向量.
O
思考:共线向量一定在一条直线上吗?
巩固练习:判断下列结论是否正确。
(1)平行向量方向一定相同; ( )
(2)不相等向量一定不平行; ( )
(3)与零向量相等的向量是零向量; ( )
(4)与任何向量都平行的向量是零向量; ( )
(5)共线向量一定在一条直线上; ( )
(6)若两向量平行,则这两向量的方向相同或相反;
( )
(7)相等向量一定是平行向量。 ( )
×
×
√
√
×
×
√
O
例1.如图,设O是正六边形ABCDEF的中心,分别写
出图中与向量 相等的向量.
问题:
(1) 与 相等吗
(2) 与 相等吗
(3)与 长度相等的向量有几个
(4)与 共线的向量有哪几个
解:
相等的有7个
长度相等的有15个
根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(1)四边形ABCD是平行四边形。
(2)四边形ABCD是菱形。
四.课堂练习
1.判断下列结论是否正确,并说明理由。
(1)单位向量都是相等向量; ( )
(2)物理学中的作用力与反作用力是一对共线向量;( )
(3)方向为南偏西60°的向量与北偏东60°的向量是共线向
量; ( )
(4)直角坐标平面上的x轴、y轴都是向量。( )
×
√
√
×
2.已知边长为3的等边三角形ABC,求BC边上的中线向量
的模 。
向量的相反向量
定义:
※注意:
零向量的相反向量仍是零向量。
(1)下列各量中是向量的是( )
A.时间 B.速度
C.面积 D. 长度
练习:
(2)等腰梯形 中,对角线 与 相交于点 ,点 、
分别在两腰 、 上, 过点 且 ,则下列等式
正确的是( )
A. B.
C. D.
B
D
(3).下列说法正确的是 ( )
A) 方向相同或相反的向量是平行向量.
B) 零向量是 .
C)长度相等的向量叫做相等向量.
D) 共线向量是在一条直线上的向量.
B
(4).已知a、b是任意两个向量,下列条件:
①a=b; ②|a|=|b|; ③a与b的方向相反;
④a=0或b=0; ⑤ a与b都是单位向量.
能判定向量a与b平行的是_____.
①③④
小结:
提问:
1.本节主要介绍了哪些概念
2.向量如何表示
