2020-2021学年 七年级数学苏科版下册 11.5 用一元一次不等式解决问题 教学课件(共23张)
文档属性
| 名称 | 2020-2021学年 七年级数学苏科版下册 11.5 用一元一次不等式解决问题 教学课件(共23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 231.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览







文档简介
第11章 一元一次不等式
11.5 用一元一次不等式解决问题
七年级数学下册苏科版
1
一元一次不等式的应用
1
新知导入
想一想:
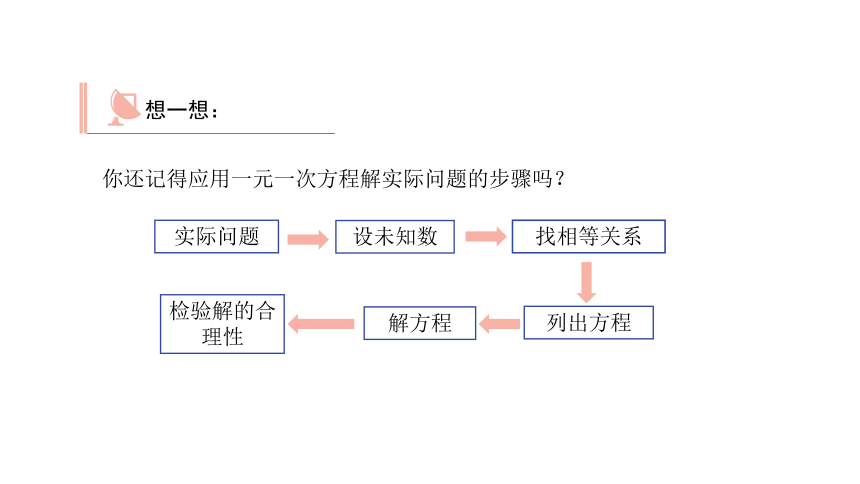
你还记得应用一元一次方程解实际问题的步骤吗?
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2
课程讲授
一元一次不等式的应用
问题1
一只纸箱质量为1 kg,当放入一些苹果(每只苹果的质量为0.25 kg)后,箱子和苹果的总质量为10 kg。这只纸箱内最多能装多少个苹果?
(1) 设纸箱内装x个苹果,则这些苹果的质量为______kg,纸箱和苹果的总质量为________kg.
0.25x
0.25x+1
一元一次不等式的应用
(2)纸箱和苹果的总质量与10 kg有什么关系?
纸箱和苹果的总质量 ≤ 10.
(3)你能用不等式把这种关系表示出来吗?
0.25x+1≤10
(4)解上面列出的不等式,并根据解集确定实际问题的答案.
解得x≤ 36,故这只纸箱内最多能装36个苹果.
一元一次不等式的应用
问题2
某种杜鹃花适宜生长在平均气温为17℃到20 ℃ 之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100m,气温下降0.6 ℃ ,求该山区适宜种植这种杜鹃花最多高多少米的山坡上?
解:设该山区适宜种植杜鹃花山坡的高度为x m.
由题意,得 20- ×0.6≥17
解得 x≤500
答:适宜种植杜鹃花的山坡高度最多为500 m.
一元一次不等式的应用
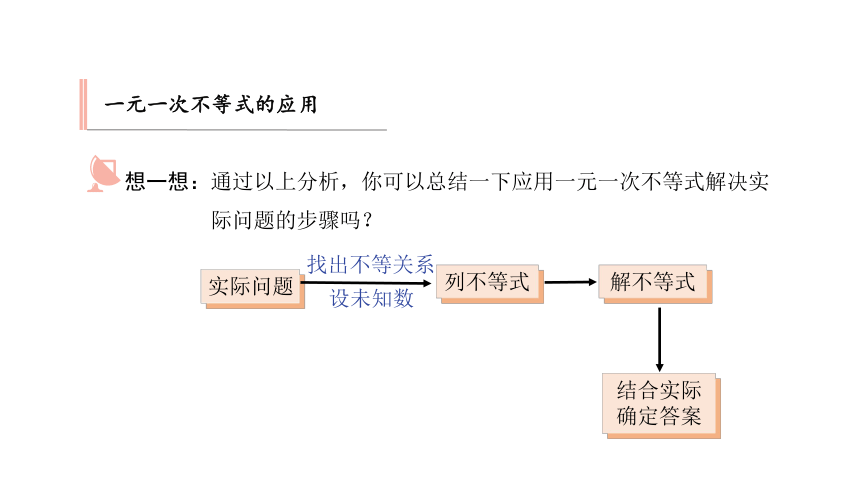
想一想:通过以上分析,你可以总结一下应用一元一次不等式解决实际问题的步骤吗?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
一元一次不等式的应用
归纳:生活中常用的不等关系与数学语言:
超过 ,至少 ,最多 .
>
≥
≤
一元一次不等式的应用
问题3
某人骑一辆变速自行车去舅舅家玩,如果行驶速度增加4 km/h,那么2 h所行驶的路程不少于以原来速度2.5 h所行驶的路程.原来行驶的速度最大是多少?
解:设原来行驶的速度为x km/h.
根据题意,得 2(x+4)≥2.5x.
解这个不等式,得
x≤16
答:原来行驶的速度最大是16 km/h.
一元一次不等式的应用
问题4
小明有些口渴了,想买瓶水喝,发现口袋里有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币?
解:设小明有1元的硬币x枚.
根据题意,得:x+0.5(13-x)<8.5.
解这个不等式,得
答:小明可能有1元硬币0枚,1枚, 2枚,3枚.
x<4
因为x是自然数,所以x可取0,1,2,3.
一元一次不等式的应用
归纳:在用不等式解决实际问题时,当求出解集后,还要根据问题的实际意义确定问题的解.
一元一次不等式的应用
练一练:某班几个同学合影留念,每人交0.7元.已知一张彩色底片0.68元,扩印一张相片0.5元,每人分一张,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人?
解析:题中的等量关系,
收来的钱=0.7元×人数
花去的钱=0.68元+0.5元×人数
题中的不等关系,
花去的钱≤收来的钱
一元一次不等式的应用
解:设这张相片上的同学有x人.
根据题意列不等式,得
0.7x≥0.68+0.5x.
解这个不等式,得
x≥3.4.
因为x为正整数,所以x至少为4.
答:这张相片上的同学至少有4人.
3
随堂练习
1.篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队预计在本赛季32场比 赛中至少得到48分,才有希望进入季后赛.假设这 个队在将要举行的比赛中胜x场,要达到目标,x 应满足的关系式是( )
A. 2x+(32-x)≥48
B. 2x-(32-x)≥48
C. 2x+(32-x)≤48
D. 2x≥48
A
2.有3人携带一批水果乘坐电梯,已知这3人的体重共210 kg,每箱水果重20 kg,电梯最大负荷为1050 kg,则该电梯在此3人乘坐的情况下最多还能搭载 箱水果.
42
3.某次知识竞赛共有20道题,每一题答对10分,答错或不答都扣5分。小明得分要超过90分,他至少要答对多少道题?
解:设小明答对x道题,则他答错或不答的题数为20-x.
根据他的得分要超过90,得10x-5(20-x)>90.
解这个不等式,得
在本题中,x应是整数而且不能超过20,
所以小明至少要答对13道题.
4. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则40x-90×40-40x·10%≥900.
解得x≥125.
答:每套童装的售价至少是125元.
5.小颖准备用21元钱买笔和笔记本。已知每枝笔3元,每个笔记本2.2元,她买了2个笔记本。请你帮她算一算,她还可能买几支笔?
解:设她还可能买x枝笔.
根据题意,得3x+2.2×2≤21.解得x≥ .
在这一问题中x只能取正整数,
所以小颖还可能买1支、2支、3支、4支或5支笔.
4
课堂小结
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
11.5 用一元一次不等式解决问题
七年级数学下册苏科版
1
一元一次不等式的应用
1
新知导入
想一想:
你还记得应用一元一次方程解实际问题的步骤吗?
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2
课程讲授
一元一次不等式的应用
问题1
一只纸箱质量为1 kg,当放入一些苹果(每只苹果的质量为0.25 kg)后,箱子和苹果的总质量为10 kg。这只纸箱内最多能装多少个苹果?
(1) 设纸箱内装x个苹果,则这些苹果的质量为______kg,纸箱和苹果的总质量为________kg.
0.25x
0.25x+1
一元一次不等式的应用
(2)纸箱和苹果的总质量与10 kg有什么关系?
纸箱和苹果的总质量 ≤ 10.
(3)你能用不等式把这种关系表示出来吗?
0.25x+1≤10
(4)解上面列出的不等式,并根据解集确定实际问题的答案.
解得x≤ 36,故这只纸箱内最多能装36个苹果.
一元一次不等式的应用
问题2
某种杜鹃花适宜生长在平均气温为17℃到20 ℃ 之间的山区。已知某山区山脚下的平均气温为20 ℃,并且每上升100m,气温下降0.6 ℃ ,求该山区适宜种植这种杜鹃花最多高多少米的山坡上?
解:设该山区适宜种植杜鹃花山坡的高度为x m.
由题意,得 20- ×0.6≥17
解得 x≤500
答:适宜种植杜鹃花的山坡高度最多为500 m.
一元一次不等式的应用
想一想:通过以上分析,你可以总结一下应用一元一次不等式解决实际问题的步骤吗?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
一元一次不等式的应用
归纳:生活中常用的不等关系与数学语言:
超过 ,至少 ,最多 .
>
≥
≤
一元一次不等式的应用
问题3
某人骑一辆变速自行车去舅舅家玩,如果行驶速度增加4 km/h,那么2 h所行驶的路程不少于以原来速度2.5 h所行驶的路程.原来行驶的速度最大是多少?
解:设原来行驶的速度为x km/h.
根据题意,得 2(x+4)≥2.5x.
解这个不等式,得
x≤16
答:原来行驶的速度最大是16 km/h.
一元一次不等式的应用
问题4
小明有些口渴了,想买瓶水喝,发现口袋里有1元和5角的硬币共13枚,这些硬币的总币值小于8.5元.问小明可能有几枚1元的硬币?
解:设小明有1元的硬币x枚.
根据题意,得:x+0.5(13-x)<8.5.
解这个不等式,得
答:小明可能有1元硬币0枚,1枚, 2枚,3枚.
x<4
因为x是自然数,所以x可取0,1,2,3.
一元一次不等式的应用
归纳:在用不等式解决实际问题时,当求出解集后,还要根据问题的实际意义确定问题的解.
一元一次不等式的应用
练一练:某班几个同学合影留念,每人交0.7元.已知一张彩色底片0.68元,扩印一张相片0.5元,每人分一张,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人?
解析:题中的等量关系,
收来的钱=0.7元×人数
花去的钱=0.68元+0.5元×人数
题中的不等关系,
花去的钱≤收来的钱
一元一次不等式的应用
解:设这张相片上的同学有x人.
根据题意列不等式,得
0.7x≥0.68+0.5x.
解这个不等式,得
x≥3.4.
因为x为正整数,所以x至少为4.
答:这张相片上的同学至少有4人.
3
随堂练习
1.篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队预计在本赛季32场比 赛中至少得到48分,才有希望进入季后赛.假设这 个队在将要举行的比赛中胜x场,要达到目标,x 应满足的关系式是( )
A. 2x+(32-x)≥48
B. 2x-(32-x)≥48
C. 2x+(32-x)≤48
D. 2x≥48
A
2.有3人携带一批水果乘坐电梯,已知这3人的体重共210 kg,每箱水果重20 kg,电梯最大负荷为1050 kg,则该电梯在此3人乘坐的情况下最多还能搭载 箱水果.
42
3.某次知识竞赛共有20道题,每一题答对10分,答错或不答都扣5分。小明得分要超过90分,他至少要答对多少道题?
解:设小明答对x道题,则他答错或不答的题数为20-x.
根据他的得分要超过90,得10x-5(20-x)>90.
解这个不等式,得
在本题中,x应是整数而且不能超过20,
所以小明至少要答对13道题.
4. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则40x-90×40-40x·10%≥900.
解得x≥125.
答:每套童装的售价至少是125元.
5.小颖准备用21元钱买笔和笔记本。已知每枝笔3元,每个笔记本2.2元,她买了2个笔记本。请你帮她算一算,她还可能买几支笔?
解:设她还可能买x枝笔.
根据题意,得3x+2.2×2≤21.解得x≥ .
在这一问题中x只能取正整数,
所以小颖还可能买1支、2支、3支、4支或5支笔.
4
课堂小结
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
