2020-2021学年七年级数学苏科版 下册 12.2 第1课时 证明(1) 教学课件(共26张)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版 下册 12.2 第1课时 证明(1) 教学课件(共26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 771.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 10:40:23 | ||
图片预览








文档简介
第12章 证 明
12.2 证 明
七年级数学下册苏科版
第1课时 证 明(1)
1
推理说明的必要性
2
证明与定理
1
新知导入
看一看:
请猜一猜老师的体重大约是多少公斤?(精确到个位)
(你猜测的依据是什么?可以如何加以验证呢?)
2
课程讲授
推理说明的必要性
问题1
下面两图中的两条线段AB与CD哪一条长一些?看一看,说一说.
D
C
B
A
A
B
C
D
推理说明的必要性
问题2
校园内一矩形草地中间有一笔直的小路(如图1),为了达到“曲径通幽”的效果,现计划修改为弯曲的小道(如图2).这两条小道的面积相等吗?
(2)
(1)
1m
1m
1m
1m
1m
1m
b m
b m
a m
a m
推理说明的必要性
m
b
m
1
b
m
(a-1)
m
如果将图2中小路右边的草坪向左平移1m,那么得到一个长为(a-1)m、宽为bm的新长方形,它的面积为b(a-1)m2.
S直= S弯
因为
所以
S弯= S矩-S草=a×b - (a - 1) ×b
=ab -ab+b=b (m2)
有根有据的说理!
推理说明的必要性
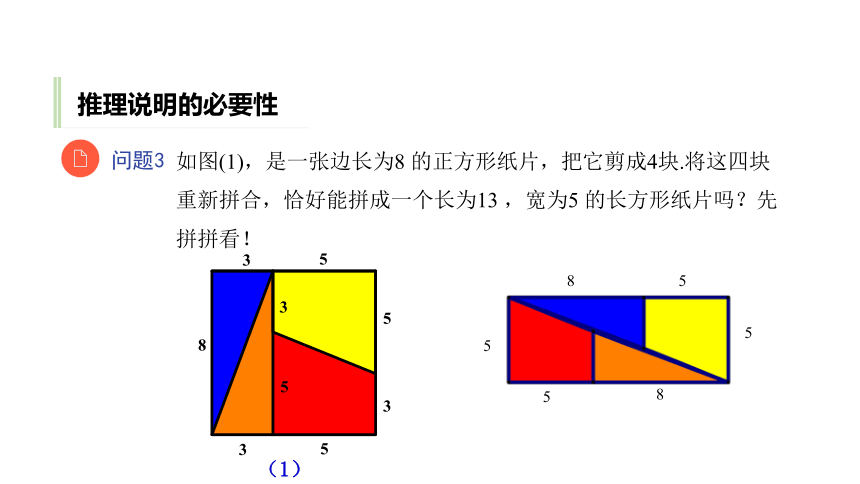
问题3
如图(1),是一张边长为8 的正方形纸片,把它剪成4块.将这四块重新拼合,恰好能拼成一个长为13 ,宽为5 的长方形纸片吗?先拼拼看!
(1)
8
8
5
5
5
5
推理说明的必要性
问题4
如图,已知∠AOB=90°,OC是∠AOB的角平分线OC.
操作1:将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,并比较PE、PF的长度;
推理说明的必要性
问题4
操作2:把三角尺绕点P旋转,再次比较PE与PF的长度.
推理说明的必要性
归纳:
通过刚才的实验、观察、操作活动,我们感受到……
实验、观察、操作是人们认识事物的重要手段.通过实验、观察、操作得到的结论常常是正确的.但是有时实验、观察、操作得到的结论是不深入的、不全面的,甚至是错误的!
很多时候证明很必要!
证明
定义:根据已知的真命题,确定某个命题真实性的过程叫做证明,经过证明的真命题称为定理.
证明
做一做:已知:如图,在直线a、b、c中,a⊥c,b⊥c.求证:a∥b
a
b
c
┐ ┐
1
2
证明:
∵a⊥c(已知),
∴∠1=90°(垂直的定义),
∵b⊥c(已知),
∴∠2=90°(角平分线的定义) ,
∴∠1=∠2 (等量代换),
∴a∥b(同位角相等,两直线平行),
证明
归纳:
证明过程必须做到言必有据.证明过程通常包含几个推理,每个推理应包括因、果和由因得果的依据.其中,“因”是已知事项;“果”是推得的结论;“由因得果的依据”是基本事实、定义、已学过的定理.以及等式性质、不等式性质等.
证明
归纳:
证明与图形有关的命题的一般步骤:
(1) 根据题意,画出图形.
(2) 根据题设、结论,结合图形,写出已知、求证.
(3) 写出证明过程
证明
例1 已知:如图,直线EF分别截AB、CD于点M、N, AB∥CD ,MG、NH分别是∠EMB与∠END的平分线.
求证:MG∥NH.
证明
证明:
∵AB∥CD(已知)
∴∠EMB=∠END(两直线平行,同位角相等)
∵MG平分∠EMB,NH平分∠END(已知)
∴∠EMG= ∠EMB,∠ENH= ∠END(角平分线的定义)
∴∠EMG=∠ENH
∴MG∥NH(同位角相等,两直线平行)
证明
已知:如图,直线l3分别与l1,l2交于点A,点B,且∠1=∠2.
求证:l1∥l2.
A
B
l1
l2
l3
(
1
)
2
)3
证明:∵ ∠1=∠2
∠3=∠2
∴ ∠1=∠3
∴ l1∥l2
(已知),
(对顶角相等),
(等量代换).
(同位角相等,两直线平行).
练一练:
3
随堂练习
1.在括号内填上理由.
已知:如图,∠A+∠B= 180°.
求证:∠C+∠D= 180°.
证明:∵∠A+∠B= 180°(已知),
∴ AD∥BC( ).
∴ ∠C+∠D= 180°
( ).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2.已知:如图,直线AB,CD被直线MN所截,∠1=∠2.
求证:∠2=∠3,∠3+∠4=180°.
证明: ∵ ∠1=∠2,
∴ ∠2 =∠3(两直线平行,内错角相等)
∠3+∠4=180°(两直线平行, 同旁内角互补).
∴ AB∥CD(同位角相等,两直线平行)
3.
A
B
C
E
F
2
1
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
A
B
C
E
F
2
1
证明:∵OE平分∠AOB,
∴∠1= ∠AOB.
∵OF平分 ∠BOC, ∴∠2= ∠BOC.
∴∠1+∠2= (∠AOB+∠BOC)
= ∠AOC = ×180°=90°.
∴OE⊥OF(垂直定义).
4
课堂小结
证明
推理说明的必要性
证明
步骤:
(1) 根据题意,画出图形.
(2) 根据题设、结论,结合图形,写出已知、求证.
(3) 写出证明过程
根据已知的真命题,确定某个命题真实性的过程叫做证明
定理
经过证明的真命题称为定理
12.2 证 明
七年级数学下册苏科版
第1课时 证 明(1)
1
推理说明的必要性
2
证明与定理
1
新知导入
看一看:
请猜一猜老师的体重大约是多少公斤?(精确到个位)
(你猜测的依据是什么?可以如何加以验证呢?)
2
课程讲授
推理说明的必要性
问题1
下面两图中的两条线段AB与CD哪一条长一些?看一看,说一说.
D
C
B
A
A
B
C
D
推理说明的必要性
问题2
校园内一矩形草地中间有一笔直的小路(如图1),为了达到“曲径通幽”的效果,现计划修改为弯曲的小道(如图2).这两条小道的面积相等吗?
(2)
(1)
1m
1m
1m
1m
1m
1m
b m
b m
a m
a m
推理说明的必要性
m
b
m
1
b
m
(a-1)
m
如果将图2中小路右边的草坪向左平移1m,那么得到一个长为(a-1)m、宽为bm的新长方形,它的面积为b(a-1)m2.
S直= S弯
因为
所以
S弯= S矩-S草=a×b - (a - 1) ×b
=ab -ab+b=b (m2)
有根有据的说理!
推理说明的必要性
问题3
如图(1),是一张边长为8 的正方形纸片,把它剪成4块.将这四块重新拼合,恰好能拼成一个长为13 ,宽为5 的长方形纸片吗?先拼拼看!
(1)
8
8
5
5
5
5
推理说明的必要性
问题4
如图,已知∠AOB=90°,OC是∠AOB的角平分线OC.
操作1:将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,并比较PE、PF的长度;
推理说明的必要性
问题4
操作2:把三角尺绕点P旋转,再次比较PE与PF的长度.
推理说明的必要性
归纳:
通过刚才的实验、观察、操作活动,我们感受到……
实验、观察、操作是人们认识事物的重要手段.通过实验、观察、操作得到的结论常常是正确的.但是有时实验、观察、操作得到的结论是不深入的、不全面的,甚至是错误的!
很多时候证明很必要!
证明
定义:根据已知的真命题,确定某个命题真实性的过程叫做证明,经过证明的真命题称为定理.
证明
做一做:已知:如图,在直线a、b、c中,a⊥c,b⊥c.求证:a∥b
a
b
c
┐ ┐
1
2
证明:
∵a⊥c(已知),
∴∠1=90°(垂直的定义),
∵b⊥c(已知),
∴∠2=90°(角平分线的定义) ,
∴∠1=∠2 (等量代换),
∴a∥b(同位角相等,两直线平行),
证明
归纳:
证明过程必须做到言必有据.证明过程通常包含几个推理,每个推理应包括因、果和由因得果的依据.其中,“因”是已知事项;“果”是推得的结论;“由因得果的依据”是基本事实、定义、已学过的定理.以及等式性质、不等式性质等.
证明
归纳:
证明与图形有关的命题的一般步骤:
(1) 根据题意,画出图形.
(2) 根据题设、结论,结合图形,写出已知、求证.
(3) 写出证明过程
证明
例1 已知:如图,直线EF分别截AB、CD于点M、N, AB∥CD ,MG、NH分别是∠EMB与∠END的平分线.
求证:MG∥NH.
证明
证明:
∵AB∥CD(已知)
∴∠EMB=∠END(两直线平行,同位角相等)
∵MG平分∠EMB,NH平分∠END(已知)
∴∠EMG= ∠EMB,∠ENH= ∠END(角平分线的定义)
∴∠EMG=∠ENH
∴MG∥NH(同位角相等,两直线平行)
证明
已知:如图,直线l3分别与l1,l2交于点A,点B,且∠1=∠2.
求证:l1∥l2.
A
B
l1
l2
l3
(
1
)
2
)3
证明:∵ ∠1=∠2
∠3=∠2
∴ ∠1=∠3
∴ l1∥l2
(已知),
(对顶角相等),
(等量代换).
(同位角相等,两直线平行).
练一练:
3
随堂练习
1.在括号内填上理由.
已知:如图,∠A+∠B= 180°.
求证:∠C+∠D= 180°.
证明:∵∠A+∠B= 180°(已知),
∴ AD∥BC( ).
∴ ∠C+∠D= 180°
( ).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2.已知:如图,直线AB,CD被直线MN所截,∠1=∠2.
求证:∠2=∠3,∠3+∠4=180°.
证明: ∵ ∠1=∠2,
∴ ∠2 =∠3(两直线平行,内错角相等)
∠3+∠4=180°(两直线平行, 同旁内角互补).
∴ AB∥CD(同位角相等,两直线平行)
3.
A
B
C
E
F
2
1
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
A
B
C
E
F
2
1
证明:∵OE平分∠AOB,
∴∠1= ∠AOB.
∵OF平分 ∠BOC, ∴∠2= ∠BOC.
∴∠1+∠2= (∠AOB+∠BOC)
= ∠AOC = ×180°=90°.
∴OE⊥OF(垂直定义).
4
课堂小结
证明
推理说明的必要性
证明
步骤:
(1) 根据题意,画出图形.
(2) 根据题设、结论,结合图形,写出已知、求证.
(3) 写出证明过程
根据已知的真命题,确定某个命题真实性的过程叫做证明
定理
经过证明的真命题称为定理
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
