2020-2021学年 七年级数学苏科版下册 12.3 互逆命题 教学课件(共25张)
文档属性
| 名称 | 2020-2021学年 七年级数学苏科版下册 12.3 互逆命题 教学课件(共25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 886.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 12:59:56 | ||
图片预览








文档简介
第12章 证 明
12.3 互逆命题
七年级数学下册苏科版
1
互逆命题
2
反例
1
新知导入
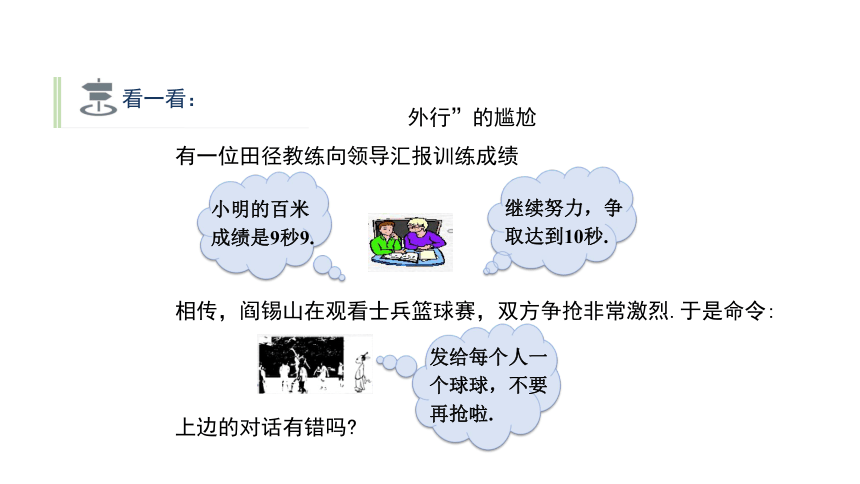
看一看:
外行”的尴尬
有一位田径教练向领导汇报训练成绩
相传,阎锡山在观看士兵篮球赛,双方争抢非常激烈.于是命令:
上边的对话有错吗?
小明的百米成绩是9秒9.
继续努力,争取达到10秒.
发给每个人一个球球,不要再抢啦.
2
课程讲授
互逆命题
问题1 对于平行线,我们知道:
两条直线被第三条直线所截,如果
这两条直线平行,那么同位角相等.
两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行.
结论
条件
条件
结论
在这两个命题中,其中一个命题的条件和结论,与另一个命题的条件和结论有怎样的关系?
互逆命题
定义:两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题是另一个命题逆命题.
互逆命题
做一做:下列各组命题是否是互逆命题:
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
(2)“等于同一个角的两个角相等”与“如果两个角都等于同一个角,那么这两个角相等”;
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
是
不是
是
不是
互逆命题
做一做:写出下列命题的逆命题.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
(4)锐角与钝角互为补角.
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
互逆命题
例 判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
提示:根据题目要求,先判断原命题的真假,再将原命题的条件和结论互换,写出原命题的逆命题,最后判断逆命题的真假.
?
互逆命题
(1)如果两条直线相交,那么它们只有一个交点;
原命题是真命题.
逆命题为:如果两条直线只有一个交点,那么它们相交.
逆命题是真命题.
(2)如果a>b,那么a2>b2;
原命题是假命题.
逆命题为:如果a2>b2,那么a>b.
逆命题是假命题.
解:
互逆命题
(3)如果两个数互为相反数,那么它们的和为零;
原命题是真命题.
逆命题为:如果两个数的和为零,那么它们互为相反数.
逆命题是真命题.
(4)如果ab<0,那么a>0,b<0.
原命题是假命题.
逆命题为:如果a>0,b<0,那么ab<0.
逆命题是真命题.
互逆命题
归纳:写出逆命题的关键是分清楚原命题的条件和结论,然后将它的条件和结论交换位置就得到这个命题的逆命题.判断一个命题是真命题需要进行逻辑推理,判断一个命题是假命题只需要举出一个反例就可以了.
互逆命题
说明:设a=-2,b=-5,(符合命题的条件)
则设a-b=-2-(-5)=3,不是负数.(不符合命题的结论)
所以“两个负数之差是负数”是假命题.
练一练:举例说明“两个负数之差是负数”是假命题.
互逆命题
例 证明:平行于同一条直线的两条直线平行.
已知:如图 ,直线a,b,c,a∥c, b∥c.
求证: a∥b.
a
b
c
作直线a、b、c的截线d.
∵b∥a (已知),
∴∠2=∠1 (两直线平行,同位角相等),
∵c∥a (已知),
∴∠3=∠1 (两直线平行,同位角相等),
∴∠2=∠3 (等量代换),
∴b∥c (同位角相等,两直线平行).
互逆命题
证明:
a
b
c
d
1
2
3
互逆命题
例 证明:直角三角形的两个锐角互余.
已知:如图,在△ABC 中,∠C=90°,
求证:∠A+∠B=90°.
A
B
C
互逆命题
证明:在△ABC 中, ∠A+∠B+∠C =180°
(三角形三个内角的和等于180°),
∴∠A +∠B = 180°- ∠C(等式性质),
∵ ∠C = 90°(已知),
∴∠A +∠B = 180°- 90°(等量代换),
∴ ∠A +∠B = 90°.
A
B
C
互逆命题
归纳:构造一个命题的逆命题,并证明这个命题是真命题,我们就能探索并获得一些新的数学结论.
这是一种逆向思考研究问题的方法.
3
随堂练习
1.(中考·无锡)写出命题“如果a=b,那么3a=3b”的逆命题______________________.
如果3a=3b,那么a=b
2.写出下列命题的逆命题
(1)如果两直线都和第三条直线垂直,那么这两直线平行;
(2)若a+b>0,则a>0,b>0;
(3)等腰三角形的两个底角相等.
(1)如果两直线平行,那么这两直线都和第三条直线垂直;
(2)若a>0,b>0,则a+b>0
(3)有两个角相等的三角形是等腰三角形.
解:
3.指出下列命题的条件和结论,并判断命题的真假,如果是假命题,请举出反例.
如果等腰三角形的两条边长为5和7,那么这个等腰三角形的周长为17.
条件:等腰三角形的两条边长为5和7,结论:这个等腰三角形的周长为17.假命题,腰长为7时,这个等腰三角形的周长为19.
4
课堂小结
互逆命题
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
12.3 互逆命题
七年级数学下册苏科版
1
互逆命题
2
反例
1
新知导入
看一看:
外行”的尴尬
有一位田径教练向领导汇报训练成绩
相传,阎锡山在观看士兵篮球赛,双方争抢非常激烈.于是命令:
上边的对话有错吗?
小明的百米成绩是9秒9.
继续努力,争取达到10秒.
发给每个人一个球球,不要再抢啦.
2
课程讲授
互逆命题
问题1 对于平行线,我们知道:
两条直线被第三条直线所截,如果
这两条直线平行,那么同位角相等.
两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行.
结论
条件
条件
结论
在这两个命题中,其中一个命题的条件和结论,与另一个命题的条件和结论有怎样的关系?
互逆命题
定义:两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题是另一个命题逆命题.
互逆命题
做一做:下列各组命题是否是互逆命题:
(1)“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”;
(2)“等于同一个角的两个角相等”与“如果两个角都等于同一个角,那么这两个角相等”;
(3)“对顶角相等”与“如果两个角相等,那么这两个角是对顶角”;
(4)“同位角相等,两直线平行”与“同位角不相等,两直线不平行” .
是
不是
是
不是
互逆命题
做一做:写出下列命题的逆命题.
(1)如果a2=b2,那么a=b;
(2)如果两个角是对顶角,那么它们的平分线组成一个平角;
(3)末位数字是5的数,能被5整除;
(4)锐角与钝角互为补角.
逆命题:如果a=b,那么a2=b2 .
逆命题:如果两个角的平分线组成一个平角,那么这两个角是对顶角.
逆命题:能被5整除的数的末位数字是5.
逆命题:互为补角的两个角一个是锐角一个是钝角.
互逆命题
例 判断下列命题的真假,写出逆命题,并判断逆命题的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
提示:根据题目要求,先判断原命题的真假,再将原命题的条件和结论互换,写出原命题的逆命题,最后判断逆命题的真假.
?
互逆命题
(1)如果两条直线相交,那么它们只有一个交点;
原命题是真命题.
逆命题为:如果两条直线只有一个交点,那么它们相交.
逆命题是真命题.
(2)如果a>b,那么a2>b2;
原命题是假命题.
逆命题为:如果a2>b2,那么a>b.
逆命题是假命题.
解:
互逆命题
(3)如果两个数互为相反数,那么它们的和为零;
原命题是真命题.
逆命题为:如果两个数的和为零,那么它们互为相反数.
逆命题是真命题.
(4)如果ab<0,那么a>0,b<0.
原命题是假命题.
逆命题为:如果a>0,b<0,那么ab<0.
逆命题是真命题.
互逆命题
归纳:写出逆命题的关键是分清楚原命题的条件和结论,然后将它的条件和结论交换位置就得到这个命题的逆命题.判断一个命题是真命题需要进行逻辑推理,判断一个命题是假命题只需要举出一个反例就可以了.
互逆命题
说明:设a=-2,b=-5,(符合命题的条件)
则设a-b=-2-(-5)=3,不是负数.(不符合命题的结论)
所以“两个负数之差是负数”是假命题.
练一练:举例说明“两个负数之差是负数”是假命题.
互逆命题
例 证明:平行于同一条直线的两条直线平行.
已知:如图 ,直线a,b,c,a∥c, b∥c.
求证: a∥b.
a
b
c
作直线a、b、c的截线d.
∵b∥a (已知),
∴∠2=∠1 (两直线平行,同位角相等),
∵c∥a (已知),
∴∠3=∠1 (两直线平行,同位角相等),
∴∠2=∠3 (等量代换),
∴b∥c (同位角相等,两直线平行).
互逆命题
证明:
a
b
c
d
1
2
3
互逆命题
例 证明:直角三角形的两个锐角互余.
已知:如图,在△ABC 中,∠C=90°,
求证:∠A+∠B=90°.
A
B
C
互逆命题
证明:在△ABC 中, ∠A+∠B+∠C =180°
(三角形三个内角的和等于180°),
∴∠A +∠B = 180°- ∠C(等式性质),
∵ ∠C = 90°(已知),
∴∠A +∠B = 180°- 90°(等量代换),
∴ ∠A +∠B = 90°.
A
B
C
互逆命题
归纳:构造一个命题的逆命题,并证明这个命题是真命题,我们就能探索并获得一些新的数学结论.
这是一种逆向思考研究问题的方法.
3
随堂练习
1.(中考·无锡)写出命题“如果a=b,那么3a=3b”的逆命题______________________.
如果3a=3b,那么a=b
2.写出下列命题的逆命题
(1)如果两直线都和第三条直线垂直,那么这两直线平行;
(2)若a+b>0,则a>0,b>0;
(3)等腰三角形的两个底角相等.
(1)如果两直线平行,那么这两直线都和第三条直线垂直;
(2)若a>0,b>0,则a+b>0
(3)有两个角相等的三角形是等腰三角形.
解:
3.指出下列命题的条件和结论,并判断命题的真假,如果是假命题,请举出反例.
如果等腰三角形的两条边长为5和7,那么这个等腰三角形的周长为17.
条件:等腰三角形的两条边长为5和7,结论:这个等腰三角形的周长为17.假命题,腰长为7时,这个等腰三角形的周长为19.
4
课堂小结
互逆命题
两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
