人教版七年级数学下册 5.3.1 平行线的性质课件(20张)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1 平行线的性质课件(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览








文档简介
5.3.1平行线的性质
判定两条直线平行的方法
同位角相等,两直线平行.
内错角相等,两直线平行.
平行于同一直线的两条直线平行.
同旁内角互补,两直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
你学会了哪些判定两条直线平行的方法?
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
E
A
C
D
B
1
2
3
4
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
平行于同一直线的两条直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
利用同位角相等,或者内错角相等,或者
同旁内角互补可以判定两条直线平行.反过来如果两条
直线平行,同位角、内错角、同旁内角各有什么关系呢?
a
b
c
1
3
2
4
8
5
7
6
动手操作,归纳性质
观察与猜想:
两条平行线被第三条直线截得的各对同位角的度数之间有什么关系?说出你的猜想:
猜想:
两条平行线被第三条直线所截,同位角___.
再任意画一条截线d,同样度量并计算
各个角的度数,你的猜想还成立吗?
相等
平行线的性质:
2.动手操作,归纳性质
性质1 两条平行线被第三条直线所截,同位角相等.
两直线平行,同位角相等.
?1
?2
3?
a
b
思考:
如右图,已知:a// b ,那么
(1)?3与?2有什么关系?为什么?
(2) ?2与?4有什么关系?为什么?
你能根据性质1,推出性质2、3吗?
?
4
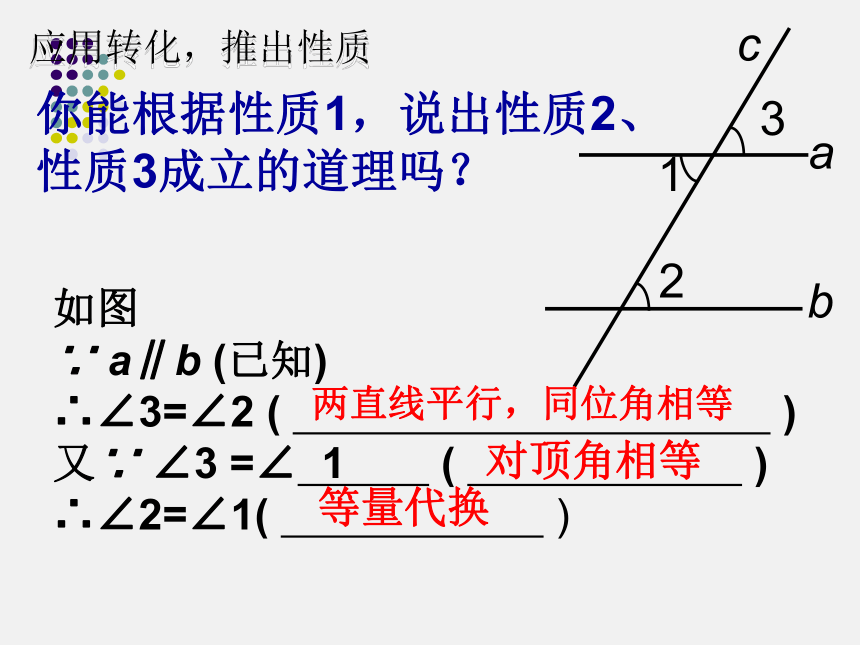
应用转化,推出性质
b
a
c
1
2
3
你能根据性质1,说出性质2、
性质3成立的道理吗?
如图
∵ a∥b (已知)
∴∠3=∠2 ( )
又∵ ∠3 =∠ 1 ( )
∴∠2=∠1( )
两直线平行,同位角相等
等量代换
对顶角相等
应用转化,推出性质
应用转化,推出性质
性质2 两条平行线被第三条直线所截,内错角相等.
平行线的性质:
两直线平行,内错角相等.
思考:
如右图,已知:a// b ,那么
(2) ?2与?4有什么关系?为什么?
你能根据性质1,推出性质2、3吗?
?1
?2
3?
a
b
?
4
应用转化,推出性质
如图
∵ a∥b (已知)
∴∠1=∠2 ( )
又∵ ∠1 +∠4=180° ( )
∴∠2+∠4=180°( )
两直线平行,同位角相等
等量代换
邻补角互补
应用转化,推出性质
性质3 两条平行线被第三条直线所截,同旁内角互补.
两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系?
两直线平行,同旁内角互补.
(1)从∠1=110?.可以知道∠2是多少度吗?为什么?
4.巩固新知,深化理解
例1 如图,平行线AB,CD被直线AE所截.
∵ AB∥CD (已知)
∴∠1=∠2 ( )
又∵ ∠1 =110? ( )
∴∠2= 110?( )
两直线平行,内错角相等
等量代换
已知
性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
平行线的性质:
简单说成:
性质1:两直线平行,同位角相等.
如果a∥b,那么∠1=∠2
性质2:两直线平行,内错角相等.
如果a∥b,那么∠2=∠3
性质3:两直线平行,同旁内角互补.
如果a∥b,那么∠2+∠4=180°
a
b
c
1
2
3
4
例 如图所示是一块梯形铁片的残余部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
解决问题:
解:
∵四边形ABCD是梯形
∴AB∥DC
(梯形的性质)
(已知)
∴∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
∴∠D =180°—∠A = 180°— 100°= 80°
∵∠A=100?, ∠B=115°
(已知)
(等量代换)
∴∠C =180°—∠B = 180°— 115°= 65°
(等量代换)
2.在下图所示的3个图中,a∥b,
分别计算∠1的度数.
D
C
A
B
1
a
a
a
b
b
b
1
1
1
36°
120°
1.如图1,AB∥CD, ∠1=45°
且∠D=∠C,
求出∠D, ∠C, ∠B的度数.
试试看:
36°
120°
巩固练习:
1.如图,直线a∥b, ∠ 1=54?,
那么∠2、∠3、∠4各是多少度?
1
2
3
4
答:∠2 = ∠ 1=54?( ),
∠4 = ∠ 1=54?( ),
∠3=180°-∠4
=180°-54°=126°( )
对顶角相等
两直线平行,同位角相等
邻补角的定义
2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )
同位角相等,两直线平行
(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.
两直线平行,同位角相等
两直线平行
判定
性质
已知
得到
得到
已知
(1)请你谈谈本节课的收获和感受。
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补
类比
直线平行的
条件
平行线的
性质
由角的大小关系转化为直线的位置关系
由直线的位置关系转化为角的大小关系
作业设计
P22 3
P23 4
判定两条直线平行的方法
同位角相等,两直线平行.
内错角相等,两直线平行.
平行于同一直线的两条直线平行.
同旁内角互补,两直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
你学会了哪些判定两条直线平行的方法?
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
E
A
C
D
B
1
2
3
4
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
平行于同一直线的两条直线平行.
在同一平面内,垂直于
同一直线的两直线平行.
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
利用同位角相等,或者内错角相等,或者
同旁内角互补可以判定两条直线平行.反过来如果两条
直线平行,同位角、内错角、同旁内角各有什么关系呢?
a
b
c
1
3
2
4
8
5
7
6
动手操作,归纳性质
观察与猜想:
两条平行线被第三条直线截得的各对同位角的度数之间有什么关系?说出你的猜想:
猜想:
两条平行线被第三条直线所截,同位角___.
再任意画一条截线d,同样度量并计算
各个角的度数,你的猜想还成立吗?
相等
平行线的性质:
2.动手操作,归纳性质
性质1 两条平行线被第三条直线所截,同位角相等.
两直线平行,同位角相等.
?1
?2
3?
a
b
思考:
如右图,已知:a// b ,那么
(1)?3与?2有什么关系?为什么?
(2) ?2与?4有什么关系?为什么?
你能根据性质1,推出性质2、3吗?
?
4
应用转化,推出性质
b
a
c
1
2
3
你能根据性质1,说出性质2、
性质3成立的道理吗?
如图
∵ a∥b (已知)
∴∠3=∠2 ( )
又∵ ∠3 =∠ 1 ( )
∴∠2=∠1( )
两直线平行,同位角相等
等量代换
对顶角相等
应用转化,推出性质
应用转化,推出性质
性质2 两条平行线被第三条直线所截,内错角相等.
平行线的性质:
两直线平行,内错角相等.
思考:
如右图,已知:a// b ,那么
(2) ?2与?4有什么关系?为什么?
你能根据性质1,推出性质2、3吗?
?1
?2
3?
a
b
?
4
应用转化,推出性质
如图
∵ a∥b (已知)
∴∠1=∠2 ( )
又∵ ∠1 +∠4=180° ( )
∴∠2+∠4=180°( )
两直线平行,同位角相等
等量代换
邻补角互补
应用转化,推出性质
性质3 两条平行线被第三条直线所截,同旁内角互补.
两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系?
两直线平行,同旁内角互补.
(1)从∠1=110?.可以知道∠2是多少度吗?为什么?
4.巩固新知,深化理解
例1 如图,平行线AB,CD被直线AE所截.
∵ AB∥CD (已知)
∴∠1=∠2 ( )
又∵ ∠1 =110? ( )
∴∠2= 110?( )
两直线平行,内错角相等
等量代换
已知
性质1:两条平行线被第三条直线所截,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
平行线的性质:
简单说成:
性质1:两直线平行,同位角相等.
如果a∥b,那么∠1=∠2
性质2:两直线平行,内错角相等.
如果a∥b,那么∠2=∠3
性质3:两直线平行,同旁内角互补.
如果a∥b,那么∠2+∠4=180°
a
b
c
1
2
3
4
例 如图所示是一块梯形铁片的残余部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
解决问题:
解:
∵四边形ABCD是梯形
∴AB∥DC
(梯形的性质)
(已知)
∴∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
∴∠D =180°—∠A = 180°— 100°= 80°
∵∠A=100?, ∠B=115°
(已知)
(等量代换)
∴∠C =180°—∠B = 180°— 115°= 65°
(等量代换)
2.在下图所示的3个图中,a∥b,
分别计算∠1的度数.
D
C
A
B
1
a
a
a
b
b
b
1
1
1
36°
120°
1.如图1,AB∥CD, ∠1=45°
且∠D=∠C,
求出∠D, ∠C, ∠B的度数.
试试看:
36°
120°
巩固练习:
1.如图,直线a∥b, ∠ 1=54?,
那么∠2、∠3、∠4各是多少度?
1
2
3
4
答:∠2 = ∠ 1=54?( ),
∠4 = ∠ 1=54?( ),
∠3=180°-∠4
=180°-54°=126°( )
对顶角相等
两直线平行,同位角相等
邻补角的定义
2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )
同位角相等,两直线平行
(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.
两直线平行,同位角相等
两直线平行
判定
性质
已知
得到
得到
已知
(1)请你谈谈本节课的收获和感受。
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补
类比
直线平行的
条件
平行线的
性质
由角的大小关系转化为直线的位置关系
由直线的位置关系转化为角的大小关系
作业设计
P22 3
P23 4
