第二十六章 反比例函数的复习 课件 -人教版九年级数学下册(共20页)
文档属性
| 名称 | 第二十六章 反比例函数的复习 课件 -人教版九年级数学下册(共20页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览





文档简介
反比例函数复习
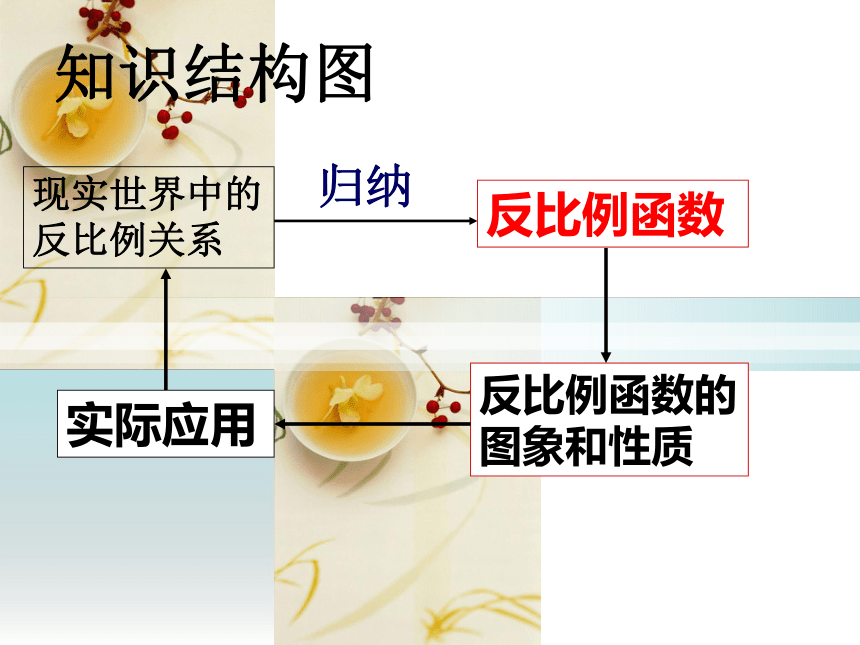
反比例函数
反比例函数的图象和性质
现实世界中的反比例关系
归纳
知识结构图
实际应用
kx-1
≠
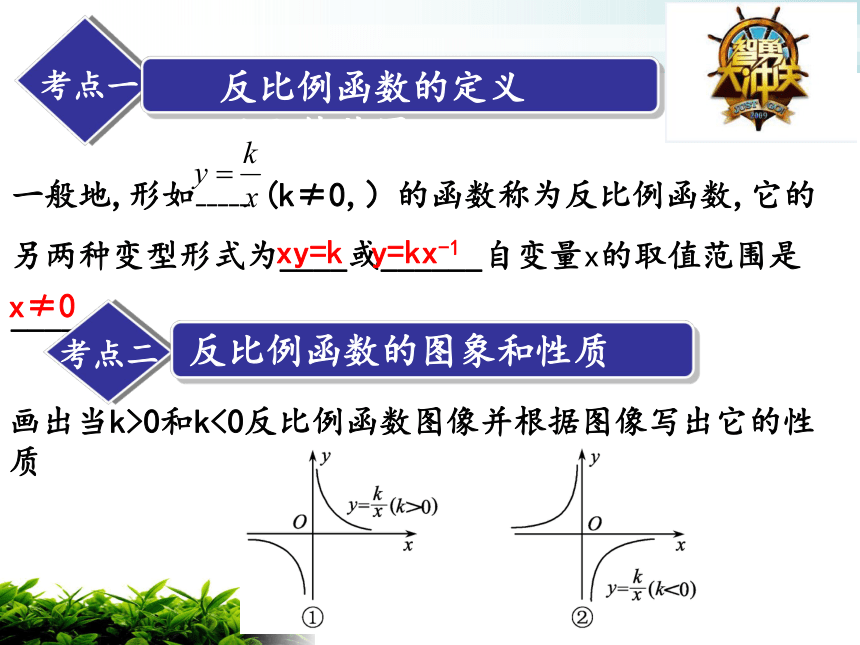
一般地,形如----- (k≠0,)的函数称为反比例函数,它的另两种变型形式为____或______自变量x的取值范围是____
考点一
反比例函数的定义及取值范围
考点二
反比例函数的图象和性质
画出当k>0和k<0反比例函数图像并根据图像写出它的性质
xy=k
y=kx-1
x≠0
●反比例函数 (k≠0)的图像是_____
因为x≠0,k≠0,相应的y值也不能为0,所以反比例函数的图像无限接近x轴和y轴,但永不与x轴、y轴____
●反比例函数 (k≠0)的图像总是关于___ 中心对称的,它的位置受k的符号影响.
●增减性:k>0,在每个象限内,图像从左到右呈___趋势,y随x的增大而___ ;k<0,在每个象限内,图像从左到右呈____趋势,y随x的增大而____.
_______
双曲线
相交
原点
下降
减小
上升
增大
反比例函数解析式的确定
考点三
反比例函数图象中比例系数k的几何意义
P(x,y)
M
o
y
x
N
反比例函数 (k≠0)中k的几何意义:双曲线 (k≠0)上任意一点P向两坐标轴作垂线,垂足分别为M、N则两垂线与坐标轴围成的矩形PNOM面积为 连接PO,则△POM(或△PON)的面积为___
基础闯关
第一关
1.已知点P(1,-3)在反比例函数 (k≠0)的图像上,则k的值是( )
A.3 B.-3 C. D.
2.对于反比例函数 ,下列说法正确的是( )
A.图像经过点(1,-3) B.图像在二、四象限
C.x>0时y随x的增大而增大 D.x<0时y随x的增大而减小
B
D
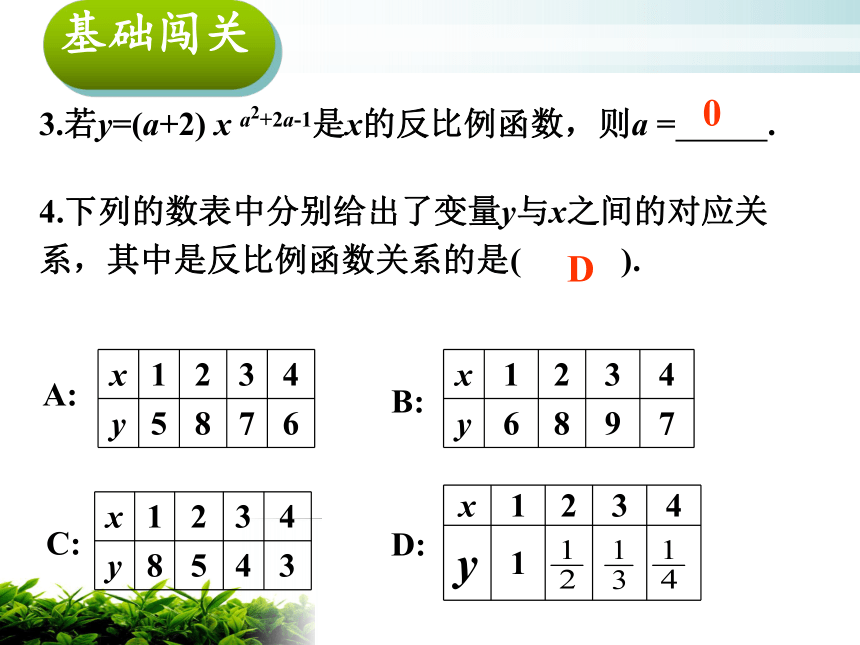
3.若y=(a+2) x a2+2a-1是x的反比例函数,则a = .
0
4.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是( ).
x
1
2
3
4
y
6
8
9
7
x
1
2
3
4
y
8
5
4
3
x
1
2
3
4
y
5
8
7
6
x
1
2
3
4
y
1
A:
C:
D:
B:
D
基础闯关
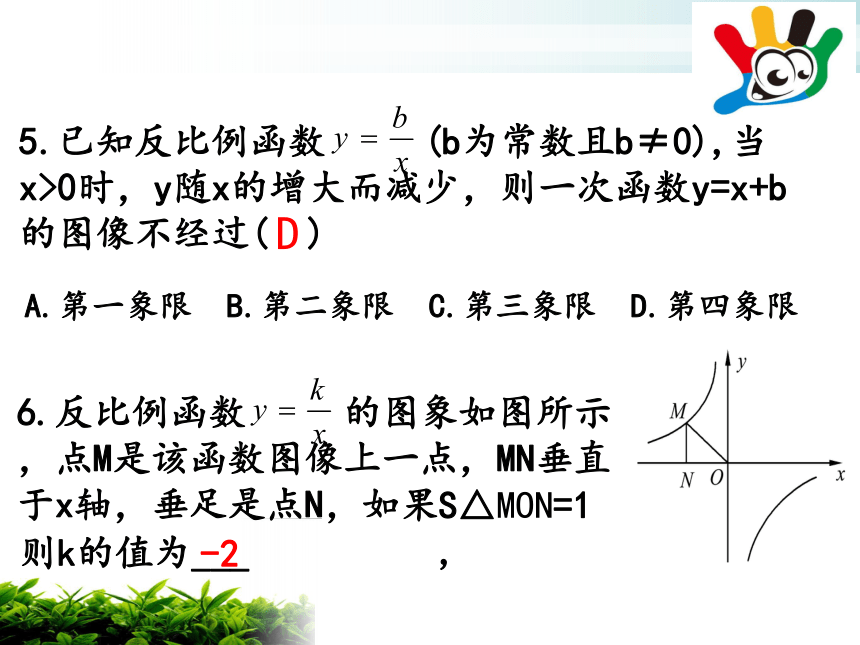
6.反比例函数 的图象如图所示,点M是该函数图像上一点,MN垂直于x轴,垂足是点N,如果
S△MON=1,
则k的值为___
-2
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知反比例函数 (b为常数且b≠0),当x>0时,y随x的增大而减少,则一次函数y=x+b的图像不经过( )
D
方法:待定系数法
由于解析式 (k≠0)因此只需已知一对对应值或一个点的坐标
考点三
考点四
反比例函数解析式的确定
7.已知y是关于x的反比例函数,当x = -3时,y = 0.6;求函数解析式和自变量x的取值范围。
因为当 x = -3 时y = 0.6,
∴y与x的函数关系式为
解:设
所以有
解得: k = -1.8
8.已知y与x+1成反比例,当x = 2时,y = -1,求函数解析式和自变量x的取值范围。
解:设
因为当 x =2 时y = -1,
所以有
解得:k = - 3
∴y与x的函数关系式为
中考闯关
已知点A(-2,y1),B(3,y2)是反比例函数 图象上的两点,则有( )
变式训练:
1
A.y1<0C.y1已知点A(-2,y1),B(-3,y2),C(4,y3)是反比例函数 (k>0)图象上的三点,则__<__<__
(比较y1,y2,y3的大小)
第二关
y1
y2
y3
B
2.考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1x<-2或x>0
解:由性质(1)得
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
双曲线
相交
减小
解决反比例函数的实际问题时,先确定函数解析式,再利用图象找出解决问题的方案,特别注意自变量的_________.
取值范围
考点五
反比例函数的应用
4.已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
o
A B C D
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
(挑战实际问题)
C
例
分析:
1、S△OPQ=S△OAP-S△OAQ或S△OPQ=S△AOB-S△OAQ-S△OBP
2、联立方程组求点P的坐标
3、代值计算
终极挑战
(成都●中考)如图所示,已知反比例函数 (k≠0)的图象经过点 ,直线y=-x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和一次函数的表达式。
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接OP、OQ、,求△OPQ的面积。
定义
图象与性质
解析式
反比例函数k的几何意义
应用
反比例函数
小结
两种方法:1、代值法 2、数形结合
一种思想:转化的思想
课后作业
1、中考数学面对面《反比例函数》
反比例函数
反比例函数的图象和性质
现实世界中的反比例关系
归纳
知识结构图
实际应用
kx-1
≠
一般地,形如----- (k≠0,)的函数称为反比例函数,它的另两种变型形式为____或______自变量x的取值范围是____
考点一
反比例函数的定义及取值范围
考点二
反比例函数的图象和性质
画出当k>0和k<0反比例函数图像并根据图像写出它的性质
xy=k
y=kx-1
x≠0
●反比例函数 (k≠0)的图像是_____
因为x≠0,k≠0,相应的y值也不能为0,所以反比例函数的图像无限接近x轴和y轴,但永不与x轴、y轴____
●反比例函数 (k≠0)的图像总是关于___ 中心对称的,它的位置受k的符号影响.
●增减性:k>0,在每个象限内,图像从左到右呈___趋势,y随x的增大而___ ;k<0,在每个象限内,图像从左到右呈____趋势,y随x的增大而____.
_______
双曲线
相交
原点
下降
减小
上升
增大
反比例函数解析式的确定
考点三
反比例函数图象中比例系数k的几何意义
P(x,y)
M
o
y
x
N
反比例函数 (k≠0)中k的几何意义:双曲线 (k≠0)上任意一点P向两坐标轴作垂线,垂足分别为M、N则两垂线与坐标轴围成的矩形PNOM面积为 连接PO,则△POM(或△PON)的面积为___
基础闯关
第一关
1.已知点P(1,-3)在反比例函数 (k≠0)的图像上,则k的值是( )
A.3 B.-3 C. D.
2.对于反比例函数 ,下列说法正确的是( )
A.图像经过点(1,-3) B.图像在二、四象限
C.x>0时y随x的增大而增大 D.x<0时y随x的增大而减小
B
D
3.若y=(a+2) x a2+2a-1是x的反比例函数,则a = .
0
4.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是( ).
x
1
2
3
4
y
6
8
9
7
x
1
2
3
4
y
8
5
4
3
x
1
2
3
4
y
5
8
7
6
x
1
2
3
4
y
1
A:
C:
D:
B:
D
基础闯关
6.反比例函数 的图象如图所示,点M是该函数图像上一点,MN垂直于x轴,垂足是点N,如果
S△MON=1,
则k的值为___
-2
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知反比例函数 (b为常数且b≠0),当x>0时,y随x的增大而减少,则一次函数y=x+b的图像不经过( )
D
方法:待定系数法
由于解析式 (k≠0)因此只需已知一对对应值或一个点的坐标
考点三
考点四
反比例函数解析式的确定
7.已知y是关于x的反比例函数,当x = -3时,y = 0.6;求函数解析式和自变量x的取值范围。
因为当 x = -3 时y = 0.6,
∴y与x的函数关系式为
解:设
所以有
解得: k = -1.8
8.已知y与x+1成反比例,当x = 2时,y = -1,求函数解析式和自变量x的取值范围。
解:设
因为当 x =2 时y = -1,
所以有
解得:k = - 3
∴y与x的函数关系式为
中考闯关
已知点A(-2,y1),B(3,y2)是反比例函数 图象上的两点,则有( )
变式训练:
1
A.y1<0
(比较y1,y2,y3的大小)
第二关
y1
y2
y3
B
2.考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1
解:由性质(1)得
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
双曲线
相交
减小
解决反比例函数的实际问题时,先确定函数解析式,再利用图象找出解决问题的方案,特别注意自变量的_________.
取值范围
考点五
反比例函数的应用
4.已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
o
A B C D
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
o
r/cm
h/cm
(挑战实际问题)
C
例
分析:
1、S△OPQ=S△OAP-S△OAQ或S△OPQ=S△AOB-S△OAQ-S△OBP
2、联立方程组求点P的坐标
3、代值计算
终极挑战
(成都●中考)如图所示,已知反比例函数 (k≠0)的图象经过点 ,直线y=-x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和一次函数的表达式。
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接OP、OQ、,求△OPQ的面积。
定义
图象与性质
解析式
反比例函数k的几何意义
应用
反比例函数
小结
两种方法:1、代值法 2、数形结合
一种思想:转化的思想
课后作业
1、中考数学面对面《反比例函数》
