6.1平行四边形的性质 课件-青岛版八年级数学下册(共14页)
文档属性
| 名称 | 6.1平行四边形的性质 课件-青岛版八年级数学下册(共14页) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览





文档简介
导学案+双色笔+课本+典
题本
还有你的激情!
课堂因你而变得精彩!
你来评一评!
1.认真研读教材,说出平行四边形的概念及其性质定理并能运用其进行计算与证明;
2.帮助老伯解决合理分地的问题,并说明依据;
3.举出一例平行四边形的性质在生活中的应用,并与同学分享.
学习目标
把握生命里的每一分钟,体验成功与感动
核心探
1.具有什么特征的四边形是平行四边形?你对 平行四边形还有哪些理解?
2.平行四边形具有哪些性质?平行四边形性质3个定理怎样推导出来的?
3.结合探究1、2,说出其中运用了平行四边形的哪些性质?你还有其它的证明方法吗?
学习指导
1.在组内交流分享自己的疑惑和见解,及时分享自己的生成.
2.针对核心重点问题运用271BAY(将探究成果修改完善后,拍照上传)+黑板自由展示;
3.展示完毕后进行小组互看;
4.针对展示较好的小组进行实时拍照、截屏保存.
5.根据提供的资源对所学内容深入探究。
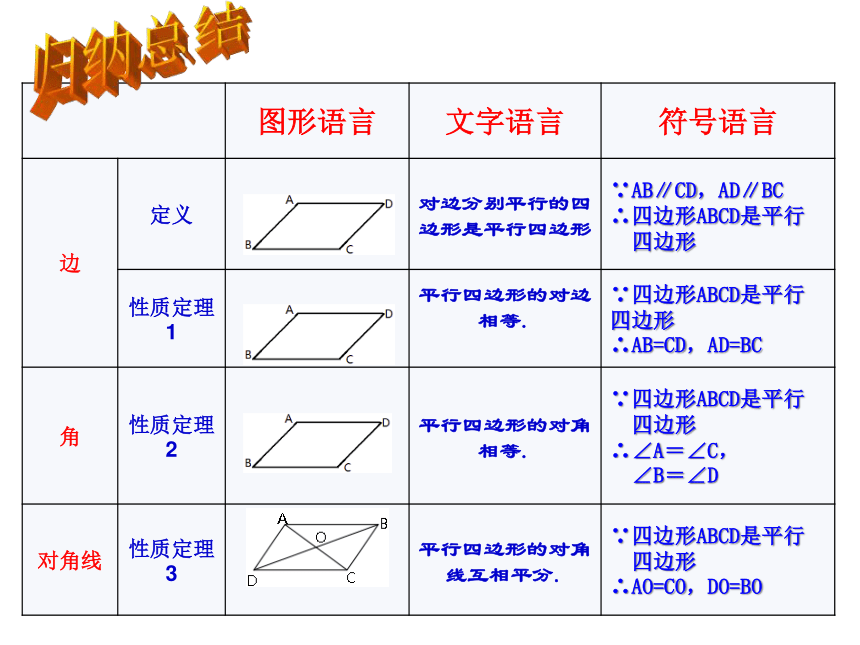
图形语言
文字语言
符号语言
边
定义
对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行
四边形
性质定理1
平行四边形的对边相等.
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
角
性质定理2
平行四边形的对角相等.
∵四边形ABCD是平行
四边形
∴∠A=∠C,
∠B=∠D
对角线
性质定理3
平行四边形的对角线互相平分.
∵四边形ABCD是平行
四边形
∴AO=CO,DO=BO
归纳总结
你来评一评!
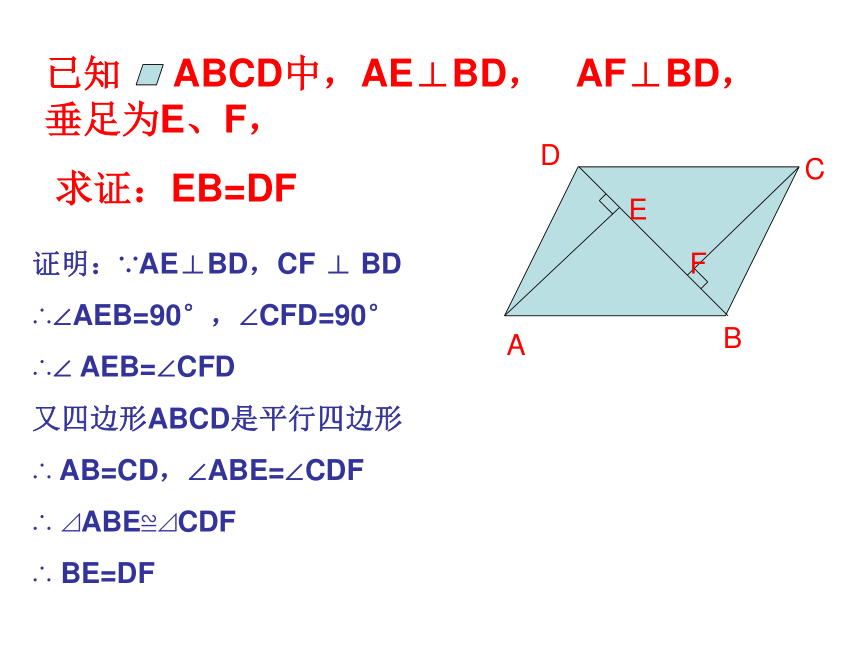
已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DF
A
B
C
D
E
F
证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF
如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF
A
B
C
D
O
E
F
证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
12
跟踪练习
如图,在平行四边形ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论.
变式训练
硕果累累
一路下来,我们学习了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
如图,在平行四边形中,对角线AC,BD交于点O,AC+BD=20,△AOB的周长等于15,则CD=____________.
5
挑战自我
如图,在平行四边形ABCD中,点E为AD的中点,CE交BA的延长线于点F,若BC=2AB,∠FBC=70°,则∠EBC的度数为多少度
当堂检测
题本
还有你的激情!
课堂因你而变得精彩!
你来评一评!
1.认真研读教材,说出平行四边形的概念及其性质定理并能运用其进行计算与证明;
2.帮助老伯解决合理分地的问题,并说明依据;
3.举出一例平行四边形的性质在生活中的应用,并与同学分享.
学习目标
把握生命里的每一分钟,体验成功与感动
核心探
1.具有什么特征的四边形是平行四边形?你对 平行四边形还有哪些理解?
2.平行四边形具有哪些性质?平行四边形性质3个定理怎样推导出来的?
3.结合探究1、2,说出其中运用了平行四边形的哪些性质?你还有其它的证明方法吗?
学习指导
1.在组内交流分享自己的疑惑和见解,及时分享自己的生成.
2.针对核心重点问题运用271BAY(将探究成果修改完善后,拍照上传)+黑板自由展示;
3.展示完毕后进行小组互看;
4.针对展示较好的小组进行实时拍照、截屏保存.
5.根据提供的资源对所学内容深入探究。
图形语言
文字语言
符号语言
边
定义
对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行
四边形
性质定理1
平行四边形的对边相等.
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
角
性质定理2
平行四边形的对角相等.
∵四边形ABCD是平行
四边形
∴∠A=∠C,
∠B=∠D
对角线
性质定理3
平行四边形的对角线互相平分.
∵四边形ABCD是平行
四边形
∴AO=CO,DO=BO
归纳总结
你来评一评!
已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DF
A
B
C
D
E
F
证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF
如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
O
D
B
A
C
●
1<AD<9
已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF
A
B
C
D
O
E
F
证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
12
跟踪练习
如图,在平行四边形ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论.
变式训练
硕果累累
一路下来,我们学习了很多新知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
如图,在平行四边形中,对角线AC,BD交于点O,AC+BD=20,△AOB的周长等于15,则CD=____________.
5
挑战自我
如图,在平行四边形ABCD中,点E为AD的中点,CE交BA的延长线于点F,若BC=2AB,∠FBC=70°,则∠EBC的度数为多少度
当堂检测
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
