_ 2020-2021学年北师大版九年级下册3.3 垂径定理课件(共25张)
文档属性
| 名称 | _ 2020-2021学年北师大版九年级下册3.3 垂径定理课件(共25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 199.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 14:00:22 | ||
图片预览




文档简介
§3.3 垂径定理
学习目标:(1分钟)
掌握垂径定理及其推论,并能运其解题.
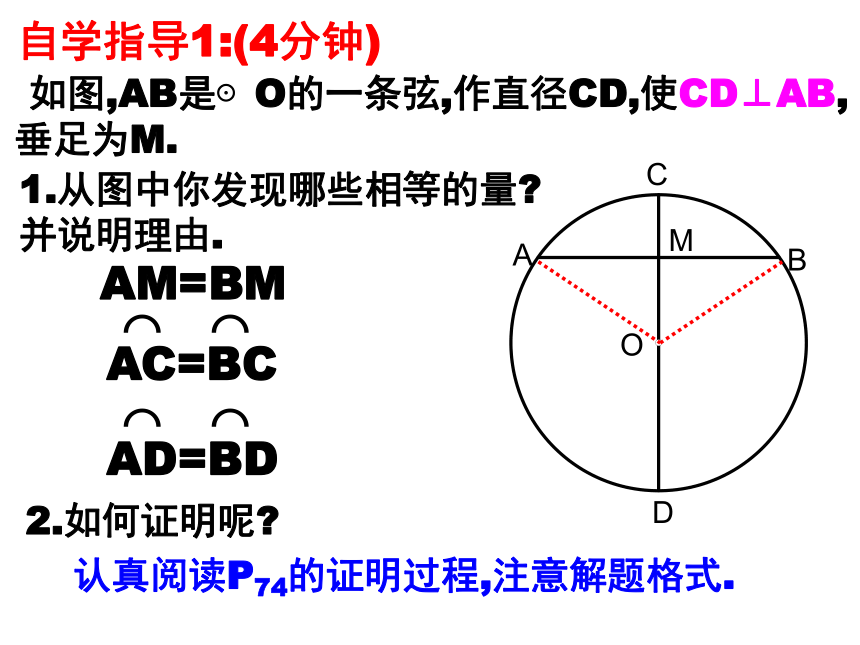
自学指导1:(4分钟)
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
1.从图中你发现哪些相等的量?并说明理由.
AM=BM
⌒
⌒
AD=BD
⌒
⌒
AC=BC
2.如何证明呢?
认真阅读P74的证明过程,注意解题格式.
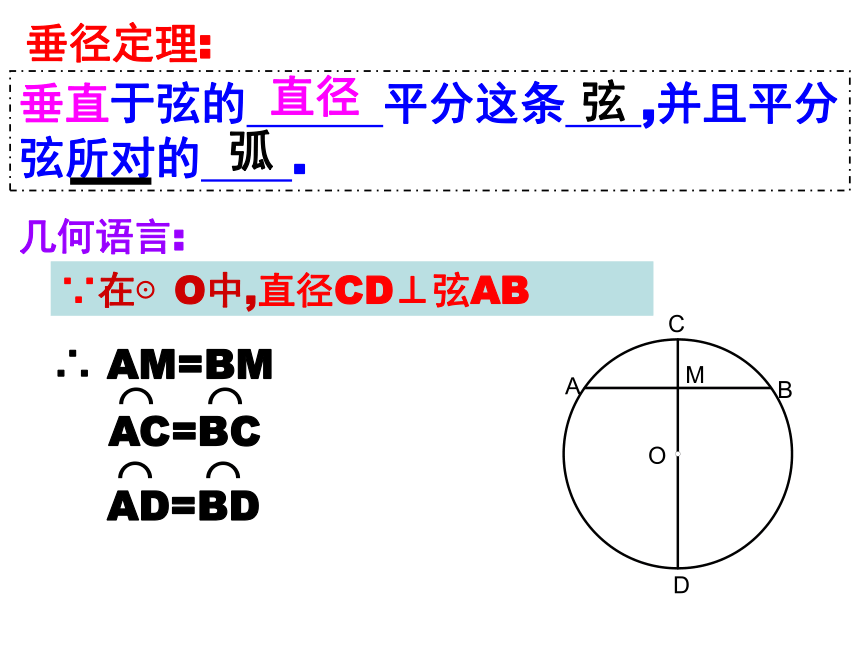
∴ AM=BM
垂直于弦的 平分这条 ,并且平分弦所对的 .
⌒
⌒
AD=BD
⌒
⌒
AC=BC
垂径定理:
直径
弦
弧
几何语言:
∵在⊙O中,CD是直径,CD⊥弦AB
∵在⊙O中,直径CD⊥弦AB
1.(2019?温州)如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是 .
应用:
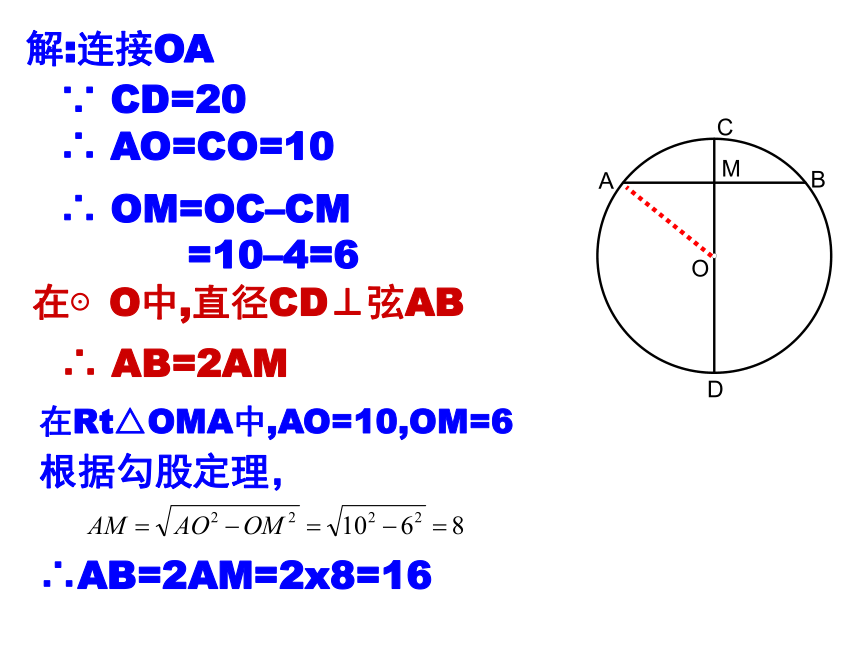
2.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=20,CM=4,则AB的长为 .
方法:围绕已知弦构造直角三角形.
解:连接OA
在⊙O中,直径CD⊥弦AB
∴ AB=2AM
∵ CD=20
∴ AO=CO=10
∴ OM=OC–CM
=10–4=6
在Rt△OMA中,AO=10,OM=6
根据勾股定理,
∴AB=2AM=2x8=16
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为 .
自学检测1:(12分钟)
2.如图为直径是52cm圆柱形油槽,装入油后,
油深CD为16cm,那么油面宽度AB= cm.
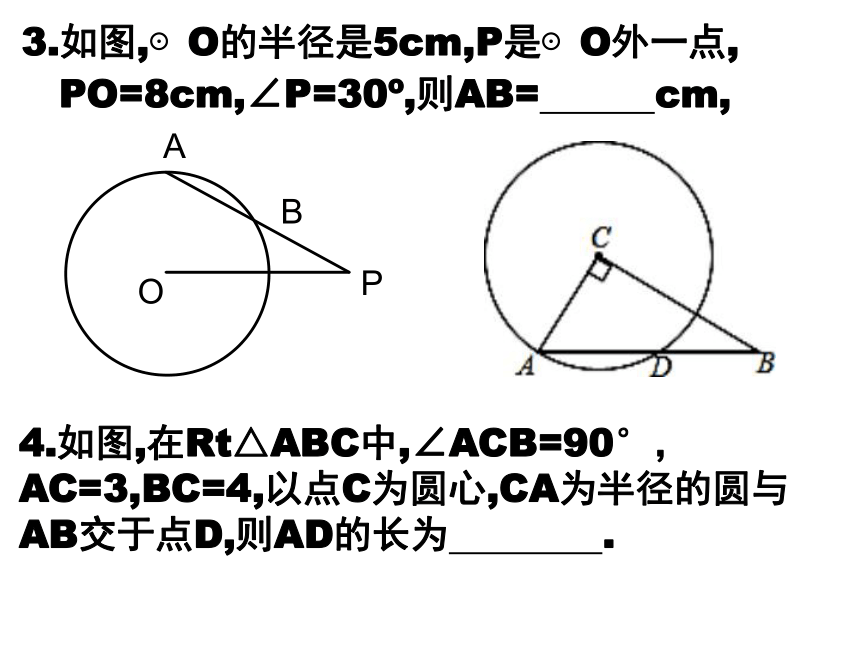
3.如图,⊙O的半径是5cm,P是⊙O外一点,
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
PO=8cm,∠P=30?,则AB= cm,
G
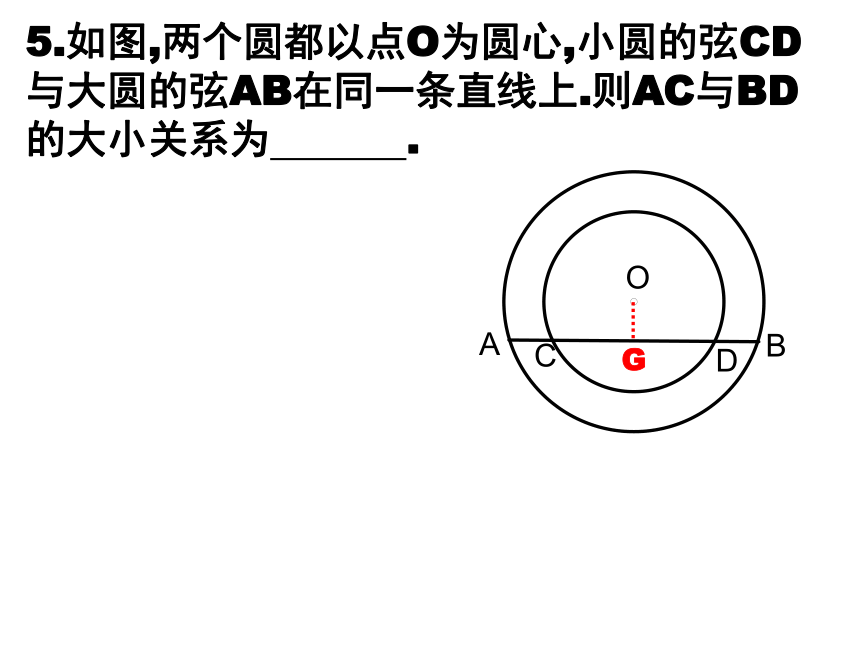
5.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.则AC与BD的大小关系为 .
变式1:如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,
求证:△OCD为等腰三角形.
E
F
E
G
变式2:如图,AB、CD是⊙O的弦,且AB∥CD.
⌒
⌒
求证:AC=BD.
自学指导2:(4+2分钟)
(一)如图,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M. 1.你能发现图中有哪些相等的量?并说明理由.
AB⊥CD
⌒
⌒
AD=BD
⌒
⌒
AC=BC
2.如何证明呢?
平分弦(不是直径)的 垂直于弦,
并且平分弦所对的弧.
垂径定理逆定理:
直径
∴AB⊥CD
⌒
⌒
AD=BD
⌒
⌒
AC=BC
∵在⊙O中,直径CD平分AB
几何语言:
1.过圆心;
2.垂直于弦;
3.平分弦;
4.平分优弧;
5.平分劣弧.
五取二有三
1.按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径, 则________,________,________;
(2)若AC=BC,MN为直径,AB不是直径, 则________,________,________;
(3)若MN⊥AB,AC=BC, 则________,________,________;
C
B
A
N
M
O
应用:(3分钟)
2.如图,AB是⊙O的一条弦,点C为弦AB的中点,OC=3,AB=8,则OA的长为 .
解得:R=545.
例:如图,一条公路的转弯处是一段圆弧(即图中弧CD,点0是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE垂直于CD,垂足为EF=90m.求这段弯路的半径.
E
O
D
C
F
解:连接OC,
设弯路的半径为Rm,则OF=(R-90)m。
∵ OE ⊥ CD
∴CF= CD= x600=300(m).
根据勾股定理,得 OC?=CF? +OF?
即 R?=300?+(R-90)?.
∴这段弯路的半径为545m.
自学检测2:(10分钟)
C
D
1.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油 后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( ) A.6分米 B.8分米
C.10分米 D.12分米
2.1300多年前,我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图).经测量,桥拱下的水面距拱顶6m时,水面宽20 m,已知桥拱跨度是14 m,运用你所学的知识计算出赵州桥的大致拱高.
2.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3, 那么BC=_______.
1.如图所示,若⊙O的半径为13cm,点是弦上一动点,且到圆心的最短距离为5cm,则弦的长为_______cm.
当堂训练:
3.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是 .
4.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
5.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,则弦AB和CD之间的距离为 .
变式:在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为 .
6.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6, 则PA+PB的最小值是 .
7.如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D,EO:OC=1:2,CD=4,求圆O的半径.
8.如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A、B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A、B,试确定此二次函数的解析式.
学习目标:(1分钟)
掌握垂径定理及其推论,并能运其解题.
自学指导1:(4分钟)
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
1.从图中你发现哪些相等的量?并说明理由.
AM=BM
⌒
⌒
AD=BD
⌒
⌒
AC=BC
2.如何证明呢?
认真阅读P74的证明过程,注意解题格式.
∴ AM=BM
垂直于弦的 平分这条 ,并且平分弦所对的 .
⌒
⌒
AD=BD
⌒
⌒
AC=BC
垂径定理:
直径
弦
弧
几何语言:
∵在⊙O中,CD是直径,CD⊥弦AB
∵在⊙O中,直径CD⊥弦AB
1.(2019?温州)如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是 .
应用:
2.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=20,CM=4,则AB的长为 .
方法:围绕已知弦构造直角三角形.
解:连接OA
在⊙O中,直径CD⊥弦AB
∴ AB=2AM
∵ CD=20
∴ AO=CO=10
∴ OM=OC–CM
=10–4=6
在Rt△OMA中,AO=10,OM=6
根据勾股定理,
∴AB=2AM=2x8=16
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为 .
自学检测1:(12分钟)
2.如图为直径是52cm圆柱形油槽,装入油后,
油深CD为16cm,那么油面宽度AB= cm.
3.如图,⊙O的半径是5cm,P是⊙O外一点,
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为 .
PO=8cm,∠P=30?,则AB= cm,
G
5.如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.则AC与BD的大小关系为 .
变式1:如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,
求证:△OCD为等腰三角形.
E
F
E
G
变式2:如图,AB、CD是⊙O的弦,且AB∥CD.
⌒
⌒
求证:AC=BD.
自学指导2:(4+2分钟)
(一)如图,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M. 1.你能发现图中有哪些相等的量?并说明理由.
AB⊥CD
⌒
⌒
AD=BD
⌒
⌒
AC=BC
2.如何证明呢?
平分弦(不是直径)的 垂直于弦,
并且平分弦所对的弧.
垂径定理逆定理:
直径
∴AB⊥CD
⌒
⌒
AD=BD
⌒
⌒
AC=BC
∵在⊙O中,直径CD平分AB
几何语言:
1.过圆心;
2.垂直于弦;
3.平分弦;
4.平分优弧;
5.平分劣弧.
五取二有三
1.按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径, 则________,________,________;
(2)若AC=BC,MN为直径,AB不是直径, 则________,________,________;
(3)若MN⊥AB,AC=BC, 则________,________,________;
C
B
A
N
M
O
应用:(3分钟)
2.如图,AB是⊙O的一条弦,点C为弦AB的中点,OC=3,AB=8,则OA的长为 .
解得:R=545.
例:如图,一条公路的转弯处是一段圆弧(即图中弧CD,点0是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE垂直于CD,垂足为EF=90m.求这段弯路的半径.
E
O
D
C
F
解:连接OC,
设弯路的半径为Rm,则OF=(R-90)m。
∵ OE ⊥ CD
∴CF= CD= x600=300(m).
根据勾股定理,得 OC?=CF? +OF?
即 R?=300?+(R-90)?.
∴这段弯路的半径为545m.
自学检测2:(10分钟)
C
D
1.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油 后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( ) A.6分米 B.8分米
C.10分米 D.12分米
2.1300多年前,我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图).经测量,桥拱下的水面距拱顶6m时,水面宽20 m,已知桥拱跨度是14 m,运用你所学的知识计算出赵州桥的大致拱高.
2.如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3, 那么BC=_______.
1.如图所示,若⊙O的半径为13cm,点是弦上一动点,且到圆心的最短距离为5cm,则弦的长为_______cm.
当堂训练:
3.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是 .
4.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
5.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,则弦AB和CD之间的距离为 .
变式:在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为 .
6.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6, 则PA+PB的最小值是 .
7.如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D,EO:OC=1:2,CD=4,求圆O的半径.
8.如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A、B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A、B,试确定此二次函数的解析式.
