2020—2021学年人教版八年级下册数学18.1.1平行四边形的性质(2) 教学课件(共16张)
文档属性
| 名称 | 2020—2021学年人教版八年级下册数学18.1.1平行四边形的性质(2) 教学课件(共16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 521.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 14:04:16 | ||
图片预览




文档简介
18.1.1平行四边形的性质
(2)
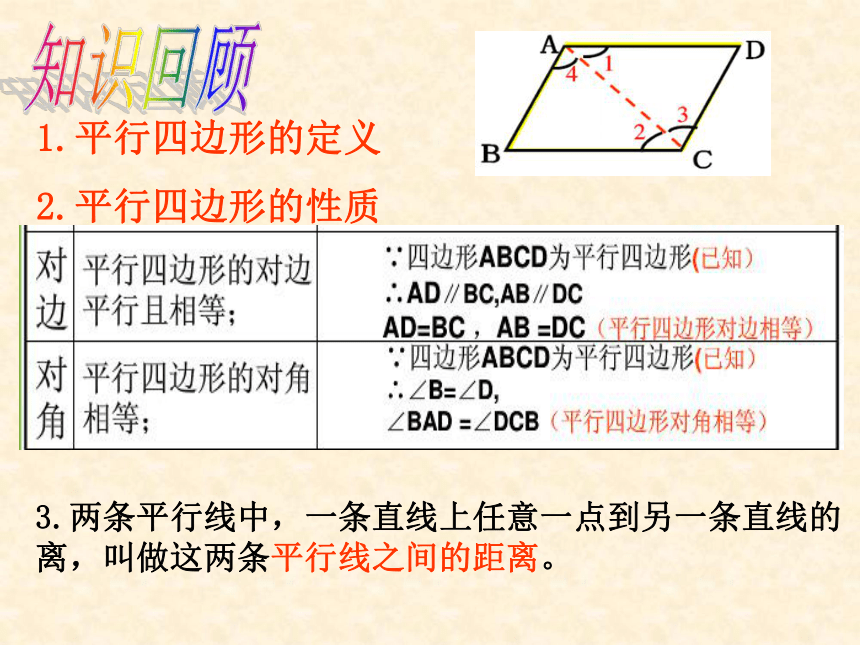
知识回顾
3.两条平行线中,一条直线上任意一点到另一条直线的
离,叫做这两条平行线之间的距离。
1.平行四边形的定义
2.平行四边形的性质
●
A
D
O
C
B
D
B
O
C
A
看一看
你有什么猜想?
结论
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是 中心对称图形,点O叫对称中心。
平行四边形的对角线互相平分.
●
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
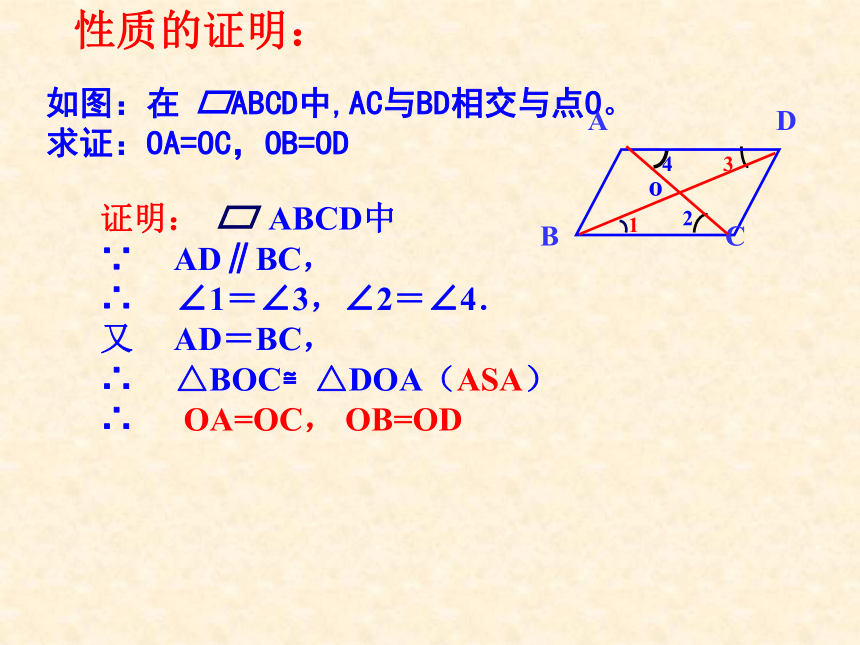
如图:在 ABCD中,AC与BD相交与点O。
求证:OA=OC,OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC, OB=OD
性质的证明:
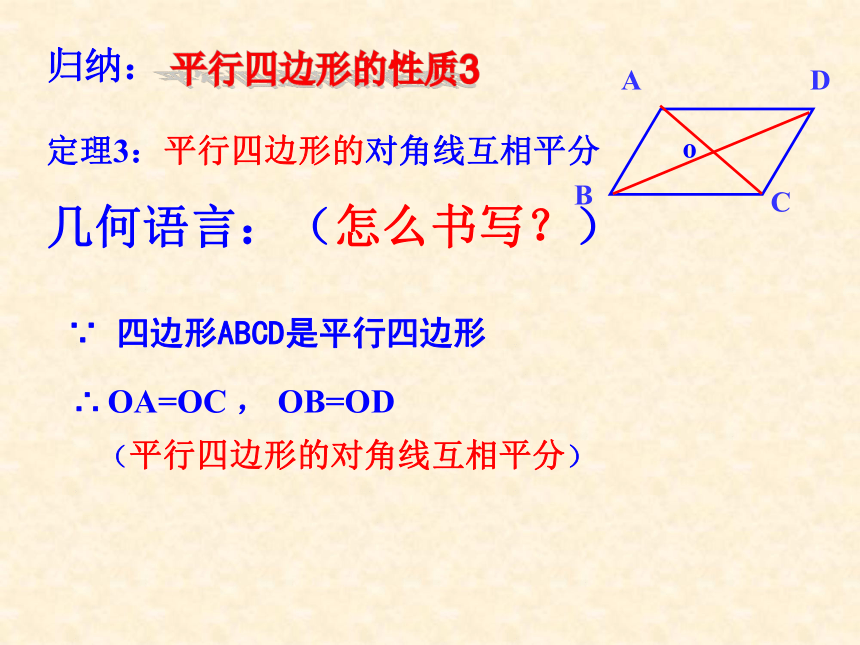
平行四边形的性质3
几何语言:(怎么书写?)
∵ 四边形ABCD是平行四边形
定理3:平行四边形的对角线互相平分
A
D
C
B
∴ OA=OC , OB=OD
(平行四边形的对角线互相平分)
o
归纳:
研究对象
研究结果
几何表示法
边
对边
邻边
角
对角
邻角
对角线
归纳:平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠BAD=∠BCD,
∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥
BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
解: 四边形ABCD是平行四边形,
BC=AD=8,CD=AB=10,
AC ⊥ BD
ABC是直角三角形。
AC= = =6
又 OA=OC,
OA= AC=3
=BC AC=8×6=48
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
AB--BC
2
2
10 -- 8
2
2
2
1
ABCD
S
·
△
E
F
图中还有哪些量相等?
变式 在上题中,直线EF过点O,且与AB,CD分
别相交于点E,F.求证:OE=OF.
A
B
C
D
O
1.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_______.
O
B
A
C
D
26cm
5
9
12
12
2. 如图:在 ABCD中,BC=10,AC=8,BD=14,△AOD的周长是 , △ABC与 △DBC的周长哪个长?
随堂练习
A
B
C
D
O
3. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
C
A
D
O
B
E
C
4.如图: ABCD的对角线AC、BD相交于点O,EF过点O与AB 、CD分别相交于点E、F。求证:OE=OF
A
B
C
D
O
E
F
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
(2)
知识回顾
3.两条平行线中,一条直线上任意一点到另一条直线的
离,叫做这两条平行线之间的距离。
1.平行四边形的定义
2.平行四边形的性质
●
A
D
O
C
B
D
B
O
C
A
看一看
你有什么猜想?
结论
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是 中心对称图形,点O叫对称中心。
平行四边形的对角线互相平分.
●
根据刚才的旋转,你知道平行四边形的对角线有什么性质吗?
猜一猜
如图:在 ABCD中,AC与BD相交与点O。
求证:OA=OC,OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC, OB=OD
性质的证明:
平行四边形的性质3
几何语言:(怎么书写?)
∵ 四边形ABCD是平行四边形
定理3:平行四边形的对角线互相平分
A
D
C
B
∴ OA=OC , OB=OD
(平行四边形的对角线互相平分)
o
归纳:
研究对象
研究结果
几何表示法
边
对边
邻边
角
对角
邻角
对角线
归纳:平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠BAD=∠BCD,
∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥
BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
解: 四边形ABCD是平行四边形,
BC=AD=8,CD=AB=10,
AC ⊥ BD
ABC是直角三角形。
AC= = =6
又 OA=OC,
OA= AC=3
=BC AC=8×6=48
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
AB--BC
2
2
10 -- 8
2
2
2
1
ABCD
S
·
△
E
F
图中还有哪些量相等?
变式 在上题中,直线EF过点O,且与AB,CD分
别相交于点E,F.求证:OE=OF.
A
B
C
D
O
1.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_______.
O
B
A
C
D
26cm
5
9
12
12
2. 如图:在 ABCD中,BC=10,AC=8,BD=14,△AOD的周长是 , △ABC与 △DBC的周长哪个长?
随堂练习
A
B
C
D
O
3. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
C
A
D
O
B
E
C
4.如图: ABCD的对角线AC、BD相交于点O,EF过点O与AB 、CD分别相交于点E、F。求证:OE=OF
A
B
C
D
O
E
F
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
