2020-2021学年八年级数学人教版下册第十八章平行四边形18.2特殊的平行四边形课后练习(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第十八章平行四边形18.2特殊的平行四边形课后练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 111.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 14:10:42 | ||
图片预览

文档简介
人教版初中数学八年级下册第十八章平行四边形18.2节特殊的平行四边形课后练习
一、单选题
1.若一个圆内接正多边形的内角是
,则这个多边形是(??
)
A.?正五边形???????????????????????????B.?正六边形???????????????????????????C.?正八边形???????????????????????????D.?正十边形
2.下列条件中,能判定一个四边形为矩形的条件是(?????
)
A.?对角线互相平分的四边形????????????????????????????????????B.?对角线相等且平分的四边形
C.?对角线相等的四边形???????????????????????????????????????????D.?对角线相等且互相垂直的四边形
3.下列说法正确的是(???
)
A.?一组对边相等,另一组对边平行的四边形是平行四边形
B.?一组邻边相等的平行四边形是矩形
C.?菱形有四条对称轴
D.?对角线相等且互相垂直平分的四边形是正方形
4.菱形的两条对角线分别为8和6,则菱形的周长和面积分别是
A.?20,48???????????????????????????????B.?14,48???????????????????????????????C.?24,20???????????????????????????????D.?20,24
5.菱形具有而矩形不具有的性质是(??
)
A.?两组对边分别平行???????????B.?对角线互相垂直???????????C.?对角线互相平分???????????D.?两组对角分别相等
6.在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为(?
)
A.?(0,﹣1)???????????????????????B.?(﹣2,1)???????????????????????C.?(2,1)???????????????????????D.?(0,﹣2)
7.正方形ABCD中,对角线AC、BD交于点O,则∠CBO等于(???
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?75°
8.若菱形的周长为8,高为1,则菱形两邻角的度数比为(??
)
A.?3∶1?????????????????????????????????????B.?4∶1?????????????????????????????????????C.?5∶1?????????????????????????????????????D.?6∶1
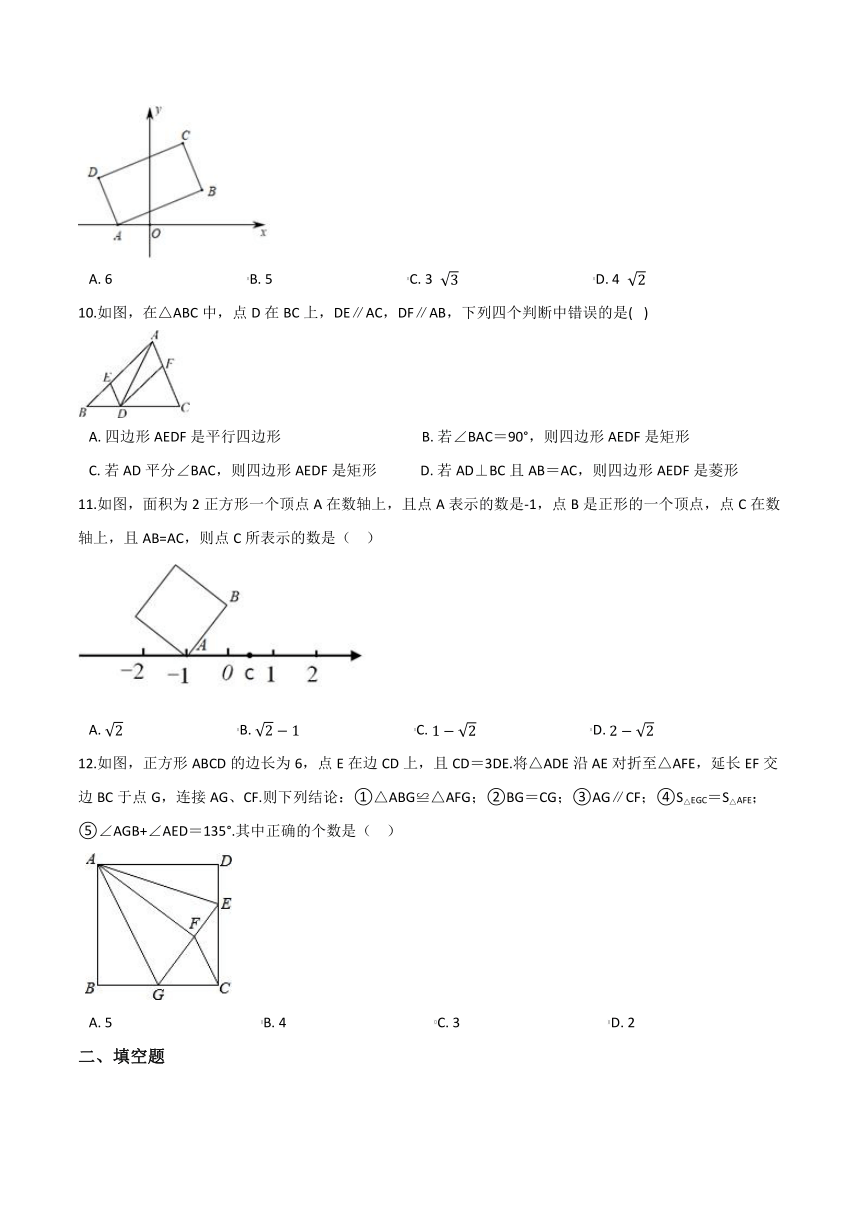
9.如图,在矩形ABCD中,点A的坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是( )
A.?6???????????????????????????????????????B.?5???????????????????????????????????????C.?3
???????????????????????????????????????D.?4
10.如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中错误的是(?
)
A.?四边形AEDF是平行四边形??????????????????????????????????
B.?若∠BAC=90°,则四边形AEDF是矩形
C.?若AD平分∠BAC,则四边形AEDF是矩形????????????D.?若AD⊥BC且AB=AC,则四边形AEDF是菱形
11.如图,面积为2正方形一个顶点A在数轴上,且点A表示的数是-1,点B是正形的一个顶点,点C在数轴上,且AB=AC,则点C所表示的数是(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
12.如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=135°.其中正确的个数是(??
)
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
二、填空题
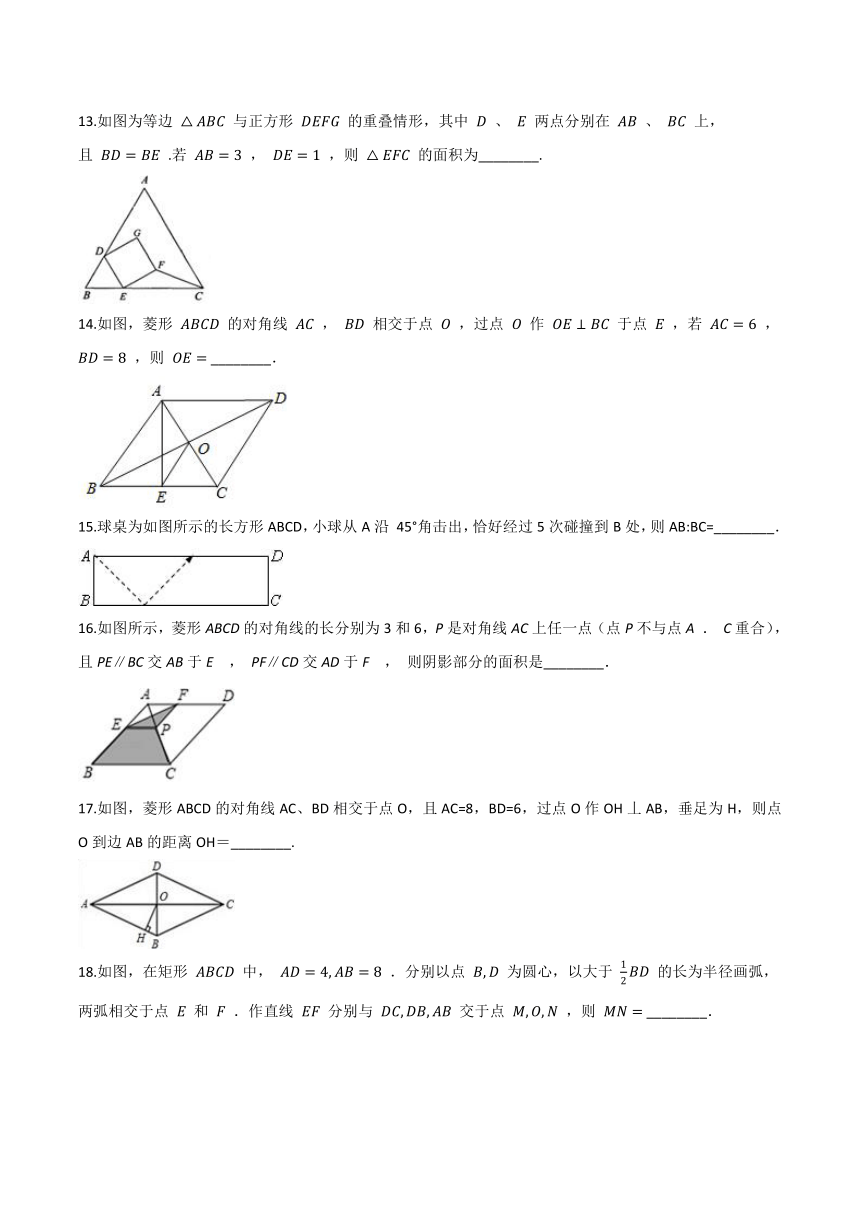
13.如图为等边
与正方形
的重叠情形,其中
、
两点分别在
、
上,且
.若
,
,则
的面积为________.
14.如图,菱形
的对角线
,
相交于点
,过点
作
于点
,若
,
,则
________.
15.球桌为如图所示的长方形ABCD,小球从A沿
45°角击出,恰好经过5次碰撞到B处,则AB:BC=________.
16.如图所示,菱形ABCD的对角线的长分别为3和6,P是对角线AC上任一点(点P不与点A
.
C重合),且PE∥BC交AB于E
,
PF∥CD交AD于F
,
则阴影部分的面积是________.
17.如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点O到边AB的距离OH=________.
18.如图,在矩形
中,
.分别以点
为圆心,以大于
的长为半径画弧,两弧相交于点
和
.作直线
分别与
交于点
,则
________.
三、解答题
19.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?为什么?
20.如图,已知
正方形
的面积为
,求
的面积.
21.如图,在
中,∠ACB=90?,∠B=60?,作边AC的垂直平分线
交AB于点D,过点C作AB的平行线交
于点E,判断四边形DBCE的形状,并说明理由.
22.如图,四边形ABCD是正方形,M为BC上一点,连接AM,延长AD至点E,使得AE=AM,过点E作EF⊥AM,垂足为F,求证:AB=EF.
参考答案
1.
A
2.
B
3.
D
4.
D
5.
B
6.
A
7.
B
8.
C
9.
B
10.
C
11.
B
12.
A
13.
14.
2.4
15.
2:5
16.
17.
18.
2
.
19.
依题意可知AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,所以纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC.
∴平行四边形ABCD为菱形;
20.
解:∵
∴∠ABC=90°
∵
∴AC=
∵正方形
的面积为
,
∴正方形
的边长FC=13cm
∵
∴
∴△AFC是直角三角形,
∴
的面积=
21.
解:四边形DBCE是菱形,理由如下:
DE垂直平分AC,
,
,即
,
,
,
四边形DBCE是平行四边形,
,
,
是
的中位线,
点D是AB的中点,
,
又
在
中,
,
,
,
平行四边形DBCE是菱形.
22.
证明:∵四边形ABCD为正方形,
∴∠B=90°,AD∥BC,
∴∠EAF=∠BMA,
∵EF⊥AM,
∴∠AFE=90°=∠B,
在△ABM和△EFA中,
∵
,
∴△ABM≌△EFA(AAS),
∴AB=EF.
一、单选题
1.若一个圆内接正多边形的内角是
,则这个多边形是(??
)
A.?正五边形???????????????????????????B.?正六边形???????????????????????????C.?正八边形???????????????????????????D.?正十边形
2.下列条件中,能判定一个四边形为矩形的条件是(?????
)
A.?对角线互相平分的四边形????????????????????????????????????B.?对角线相等且平分的四边形
C.?对角线相等的四边形???????????????????????????????????????????D.?对角线相等且互相垂直的四边形
3.下列说法正确的是(???
)
A.?一组对边相等,另一组对边平行的四边形是平行四边形
B.?一组邻边相等的平行四边形是矩形
C.?菱形有四条对称轴
D.?对角线相等且互相垂直平分的四边形是正方形
4.菱形的两条对角线分别为8和6,则菱形的周长和面积分别是
A.?20,48???????????????????????????????B.?14,48???????????????????????????????C.?24,20???????????????????????????????D.?20,24
5.菱形具有而矩形不具有的性质是(??
)
A.?两组对边分别平行???????????B.?对角线互相垂直???????????C.?对角线互相平分???????????D.?两组对角分别相等
6.在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为(?
)
A.?(0,﹣1)???????????????????????B.?(﹣2,1)???????????????????????C.?(2,1)???????????????????????D.?(0,﹣2)
7.正方形ABCD中,对角线AC、BD交于点O,则∠CBO等于(???
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?75°
8.若菱形的周长为8,高为1,则菱形两邻角的度数比为(??
)
A.?3∶1?????????????????????????????????????B.?4∶1?????????????????????????????????????C.?5∶1?????????????????????????????????????D.?6∶1
9.如图,在矩形ABCD中,点A的坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是( )
A.?6???????????????????????????????????????B.?5???????????????????????????????????????C.?3
???????????????????????????????????????D.?4
10.如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中错误的是(?
)
A.?四边形AEDF是平行四边形??????????????????????????????????
B.?若∠BAC=90°,则四边形AEDF是矩形
C.?若AD平分∠BAC,则四边形AEDF是矩形????????????D.?若AD⊥BC且AB=AC,则四边形AEDF是菱形
11.如图,面积为2正方形一个顶点A在数轴上,且点A表示的数是-1,点B是正形的一个顶点,点C在数轴上,且AB=AC,则点C所表示的数是(??
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
12.如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=135°.其中正确的个数是(??
)
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
二、填空题
13.如图为等边
与正方形
的重叠情形,其中
、
两点分别在
、
上,且
.若
,
,则
的面积为________.
14.如图,菱形
的对角线
,
相交于点
,过点
作
于点
,若
,
,则
________.
15.球桌为如图所示的长方形ABCD,小球从A沿
45°角击出,恰好经过5次碰撞到B处,则AB:BC=________.
16.如图所示,菱形ABCD的对角线的长分别为3和6,P是对角线AC上任一点(点P不与点A
.
C重合),且PE∥BC交AB于E
,
PF∥CD交AD于F
,
则阴影部分的面积是________.
17.如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点O到边AB的距离OH=________.
18.如图,在矩形
中,
.分别以点
为圆心,以大于
的长为半径画弧,两弧相交于点
和
.作直线
分别与
交于点
,则
________.
三、解答题
19.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?为什么?
20.如图,已知
正方形
的面积为
,求
的面积.
21.如图,在
中,∠ACB=90?,∠B=60?,作边AC的垂直平分线
交AB于点D,过点C作AB的平行线交
于点E,判断四边形DBCE的形状,并说明理由.
22.如图,四边形ABCD是正方形,M为BC上一点,连接AM,延长AD至点E,使得AE=AM,过点E作EF⊥AM,垂足为F,求证:AB=EF.
参考答案
1.
A
2.
B
3.
D
4.
D
5.
B
6.
A
7.
B
8.
C
9.
B
10.
C
11.
B
12.
A
13.
14.
2.4
15.
2:5
16.
17.
18.
2
.
19.
依题意可知AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,所以纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC.
∴平行四边形ABCD为菱形;
20.
解:∵
∴∠ABC=90°
∵
∴AC=
∵正方形
的面积为
,
∴正方形
的边长FC=13cm
∵
∴
∴△AFC是直角三角形,
∴
的面积=
21.
解:四边形DBCE是菱形,理由如下:
DE垂直平分AC,
,
,即
,
,
,
四边形DBCE是平行四边形,
,
,
是
的中位线,
点D是AB的中点,
,
又
在
中,
,
,
,
平行四边形DBCE是菱形.
22.
证明:∵四边形ABCD为正方形,
∴∠B=90°,AD∥BC,
∴∠EAF=∠BMA,
∵EF⊥AM,
∴∠AFE=90°=∠B,
在△ABM和△EFA中,
∵
,
∴△ABM≌△EFA(AAS),
∴AB=EF.
