_ 2020-2021学年北师大版九年级数学下册3.5 确定圆的条件课件 (26张)
文档属性
| 名称 | _ 2020-2021学年北师大版九年级数学下册3.5 确定圆的条件课件 (26张) |  | |
| 格式 | ppt | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 14:29:33 | ||
图片预览




文档简介
1.过一点可以作几条直线?
2.过几点可确定一条直线?
知识回顾:1分钟
●A
●A
●B
无数条
一条
经过几点能确定一个圆?
3.5 确定圆的条件
学习目标:(1分钟)
1.经历不在同一直线上的三个点确定一个圆的探索过程;
2.了解不在同一直线上的三个点确定一个圆,掌握作图方法;
3.了解外接圆、外心概念及其性质.
阅读P85-86的内容,并思考:
1.探索不在同一直线上的三个点如何确定一个圆;
2.掌握过不在同一直线上的三个点作一个圆的作图方法;
自学指导1:(4分钟)
A
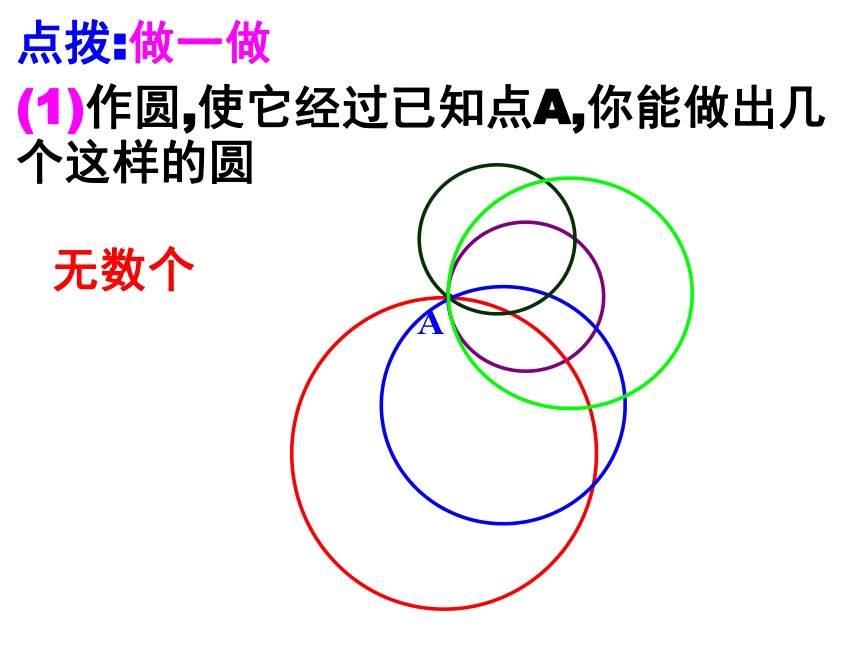
(1)作圆,使它经过已知点A,你能做出几个这样的圆
点拨:做一做
无数个
●A
●B
●O
●O
●O
●O
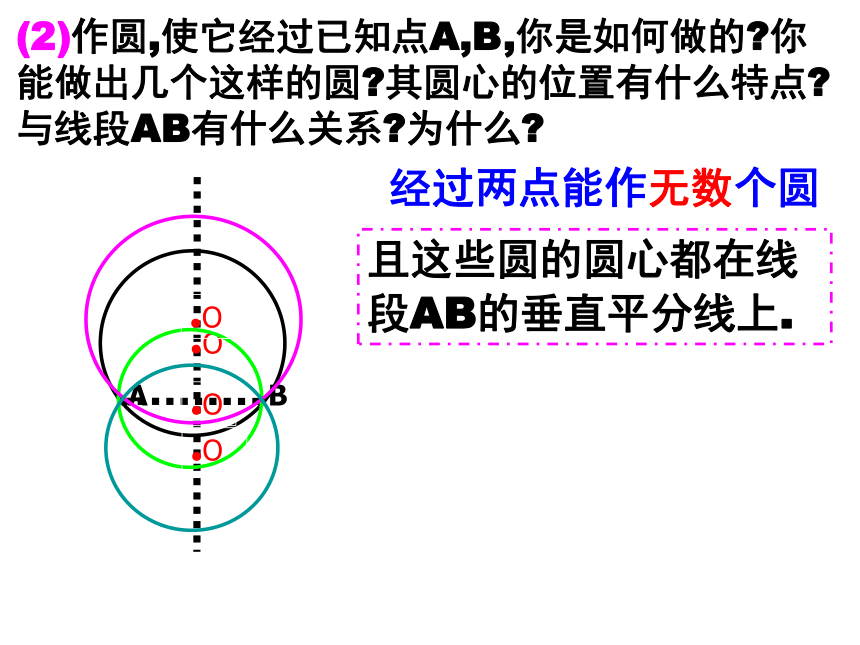
(2)作圆,使它经过已知点A,B,你是如何做的?你能做出几个这样的圆?其圆心的位置有什么特点?与线段AB有什么关系?为什么?
经过两点能作无数个圆
且这些圆的圆心都在线段AB的垂直平分线上.
O
N
M
F
E
A
B
C
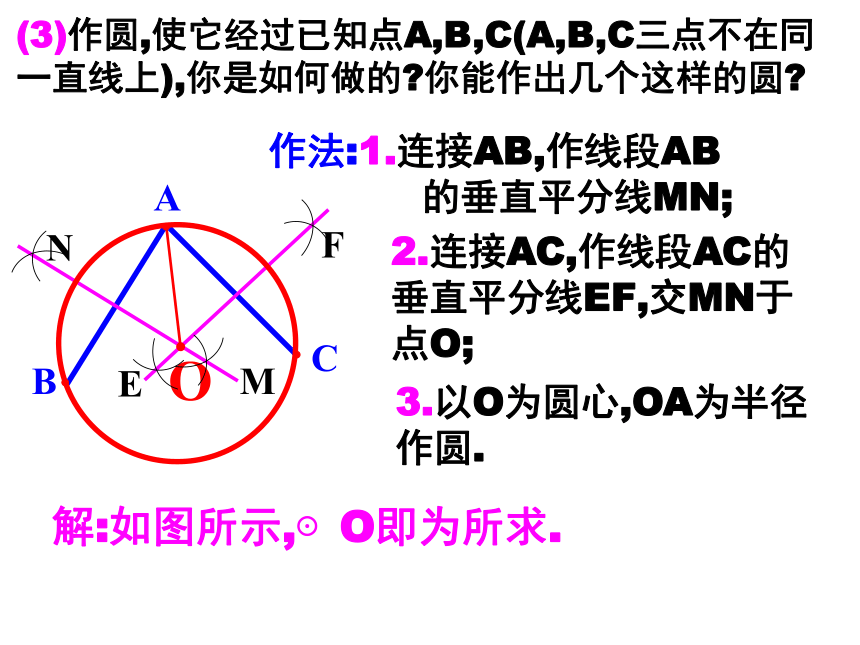
解:如图所示,⊙O即为所求.
作法:1.连接AB,作线段AB
的垂直平分线MN;
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OA为半径 作圆.
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一直线上),你是如何做的?你能作出几个这样的圆?
A
B
C
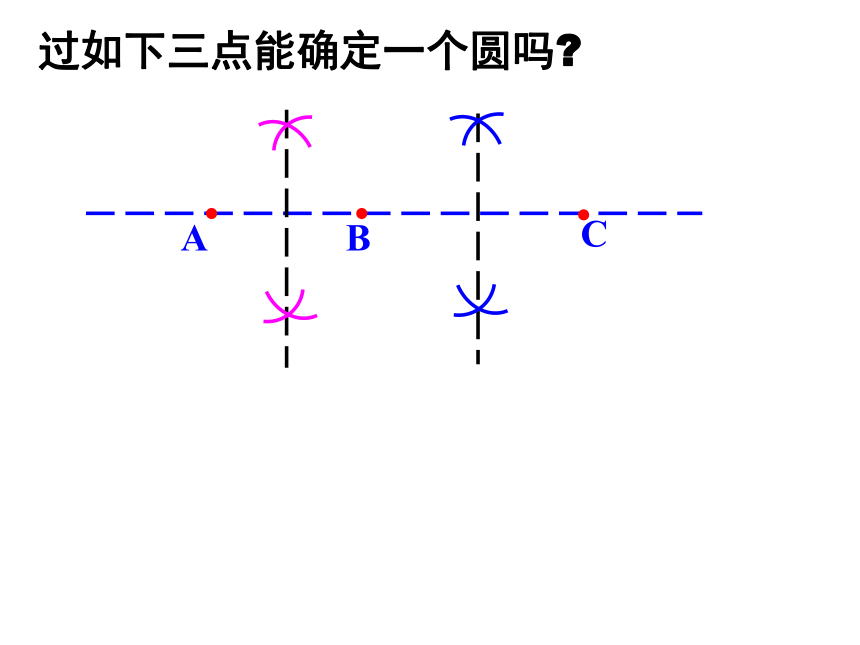
过如下三点能确定一个圆吗?
定理: 的 确定一个圆.
不在同一直线上
三点
O
A
B
C
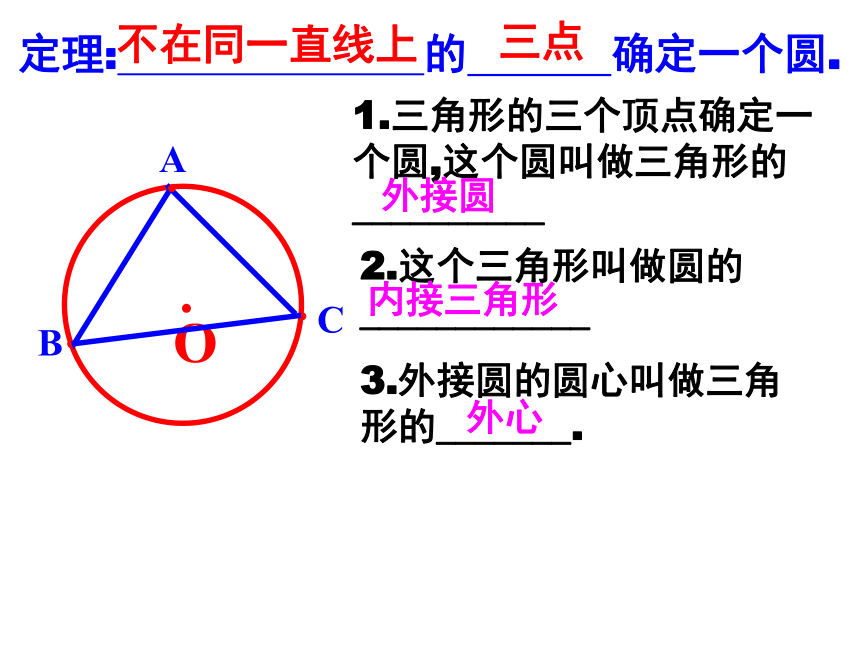
1.三角形的三个顶点确定一个圆,这个圆叫做三角形的__________
外接圆
2.这个三角形叫做圆的____________
内接三角形
3.外接圆的圆心叫做三角形的_______.
外心
C
A
B
(4)你能用尺规作图作出△ABC的外心O吗?
O
解:如图所示,点O即为所求
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
1.锐角三角形的外心位于三角形内.
2.直角三角形的外心位于直角三角形斜边中点.
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
归纳:
1.现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1.在圆弧上任取三点A、B、C;
A
B
C
O
2.作线段AB、BC的垂直平分线,其交点O即为圆心;
3.以点O为圆心,OC长为半径作圆.
解:如图所示,⊙O即为所求.
自学检测1:(10分钟)
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
B
3.如图,破残的圆形轮片上,弦AB的垂直平分线交圆于点C,交AB于点D,已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
o
4.如图,在5×5正方形网格中,一条圆弧经过A,B.C三点,那么这条圆弧所在圆的圆心是 .
变式1:如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为 (-2,4),则该圆弧所在圆的圆心坐标是 .
A
C
B
O
P
(-1,1)
变式2:如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,-2),则△ABC外接圆的圆心坐标是 .
5.图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心.
C
A
B
D
1.下面四个命题中真命题的个数是( )
①经过三点一定可以做圆;
②任意一个三角形一定有一个外接圆,而且只有一个外接圆;
③任意一个圆一定有一个内接三角形,而且只有一个内接三角形;
④三角形的外心到三角形三个顶点的距离相等.
A.4个 B.3个 C.2个 D.1个
C
自学检测2:(15分钟)
2.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1
B.a=5, b=12,c=12
C.a=5, b=12,c=13
D.a=5, b=12,c=14
C
求出△ABC外接圆的半径.
B
C
A
M
变式1:若直角三角形的两直角边长分别为6,8, 则这个三角形的外接圆直径是 .
变式2:若直角三角形的两边长分别为6,8,则这个三角形的外接圆直径是 .
3.等边△ABC边长为4,则△ABC外接圆的 面积为 .
4.在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
5.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是_________.
6.已知等腰△ABC内接于半径为5的⊙O,如果底边BC的长为6,则底角的正切值为________.
7.已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,
BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
1.如图,在Rt△ABC中,∠ACB=90°,AC=5,
CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE; (2)求BE的长; (3)求△ACD外接圆的直径.
中考链接
2.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为BD弧的中点,AC、BD交于点E.
(1)求证:△CBE∽△CAB;
(2)若S△CBE:S△CAB=1:4,求sin∠ABD的值.
2.过几点可确定一条直线?
知识回顾:1分钟
●A
●A
●B
无数条
一条
经过几点能确定一个圆?
3.5 确定圆的条件
学习目标:(1分钟)
1.经历不在同一直线上的三个点确定一个圆的探索过程;
2.了解不在同一直线上的三个点确定一个圆,掌握作图方法;
3.了解外接圆、外心概念及其性质.
阅读P85-86的内容,并思考:
1.探索不在同一直线上的三个点如何确定一个圆;
2.掌握过不在同一直线上的三个点作一个圆的作图方法;
自学指导1:(4分钟)
A
(1)作圆,使它经过已知点A,你能做出几个这样的圆
点拨:做一做
无数个
●A
●B
●O
●O
●O
●O
(2)作圆,使它经过已知点A,B,你是如何做的?你能做出几个这样的圆?其圆心的位置有什么特点?与线段AB有什么关系?为什么?
经过两点能作无数个圆
且这些圆的圆心都在线段AB的垂直平分线上.
O
N
M
F
E
A
B
C
解:如图所示,⊙O即为所求.
作法:1.连接AB,作线段AB
的垂直平分线MN;
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OA为半径 作圆.
(3)作圆,使它经过已知点A,B,C(A,B,C三点不在同一直线上),你是如何做的?你能作出几个这样的圆?
A
B
C
过如下三点能确定一个圆吗?
定理: 的 确定一个圆.
不在同一直线上
三点
O
A
B
C
1.三角形的三个顶点确定一个圆,这个圆叫做三角形的__________
外接圆
2.这个三角形叫做圆的____________
内接三角形
3.外接圆的圆心叫做三角形的_______.
外心
C
A
B
(4)你能用尺规作图作出△ABC的外心O吗?
O
解:如图所示,点O即为所求
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
1.锐角三角形的外心位于三角形内.
2.直角三角形的外心位于直角三角形斜边中点.
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
归纳:
1.现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1.在圆弧上任取三点A、B、C;
A
B
C
O
2.作线段AB、BC的垂直平分线,其交点O即为圆心;
3.以点O为圆心,OC长为半径作圆.
解:如图所示,⊙O即为所求.
自学检测1:(10分钟)
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
B
3.如图,破残的圆形轮片上,弦AB的垂直平分线交圆于点C,交AB于点D,已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
o
4.如图,在5×5正方形网格中,一条圆弧经过A,B.C三点,那么这条圆弧所在圆的圆心是 .
变式1:如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为 (-2,4),则该圆弧所在圆的圆心坐标是 .
A
C
B
O
P
(-1,1)
变式2:如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,-2),则△ABC外接圆的圆心坐标是 .
5.图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心.
C
A
B
D
1.下面四个命题中真命题的个数是( )
①经过三点一定可以做圆;
②任意一个三角形一定有一个外接圆,而且只有一个外接圆;
③任意一个圆一定有一个内接三角形,而且只有一个内接三角形;
④三角形的外心到三角形三个顶点的距离相等.
A.4个 B.3个 C.2个 D.1个
C
自学检测2:(15分钟)
2.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1
B.a=5, b=12,c=12
C.a=5, b=12,c=13
D.a=5, b=12,c=14
C
求出△ABC外接圆的半径.
B
C
A
M
变式1:若直角三角形的两直角边长分别为6,8, 则这个三角形的外接圆直径是 .
变式2:若直角三角形的两边长分别为6,8,则这个三角形的外接圆直径是 .
3.等边△ABC边长为4,则△ABC外接圆的 面积为 .
4.在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
5.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是_________.
6.已知等腰△ABC内接于半径为5的⊙O,如果底边BC的长为6,则底角的正切值为________.
7.已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,
BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
1.如图,在Rt△ABC中,∠ACB=90°,AC=5,
CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE; (2)求BE的长; (3)求△ACD外接圆的直径.
中考链接
2.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,C为BD弧的中点,AC、BD交于点E.
(1)求证:△CBE∽△CAB;
(2)若S△CBE:S△CAB=1:4,求sin∠ABD的值.
