_2020-2021学年北师大版九年级数学下册3.2圆的对称性课件(23张)
文档属性
| 名称 | _2020-2021学年北师大版九年级数学下册3.2圆的对称性课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览




文档简介
§3.2 圆的对称性
学习目标:(1分钟)
1.理解圆的对称性; 2.掌握圆心角、弧、弦、弦心距间的关系,并能用其解题.
认真阅读P70-71例题前的内容,并思考:
1.圆是轴对称图形,对称轴是 ,有 __条对称轴;
2.圆是中心对称图形吗?对称中心是______;
3.理解圆的旋转不变性; 4.理解:圆心角、弧、弦、弦心距间的关系.
自学指导1:(4分钟)
1.圆是轴对称图形吗?
2.如果是,它的对称轴是什么?你能找到多少条对称轴?
●O
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
3.圆是中心对称图形吗?
圆是中心对称图形.
对称中心为圆心
点拨:
圆绕圆心旋转任意角度与原图形重合.
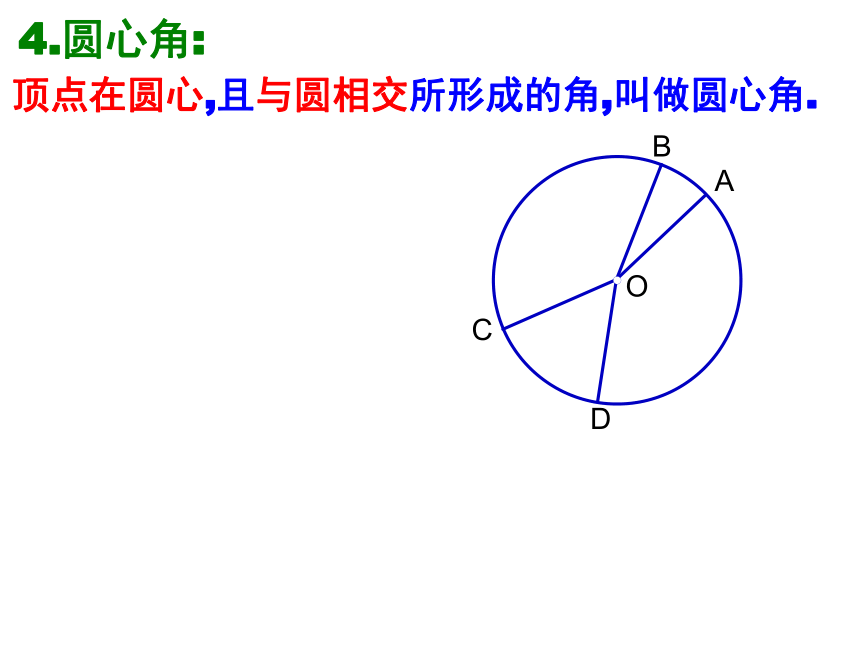
4.圆心角:
顶点在圆心,且与圆相交所形成的角,叫做圆心角.
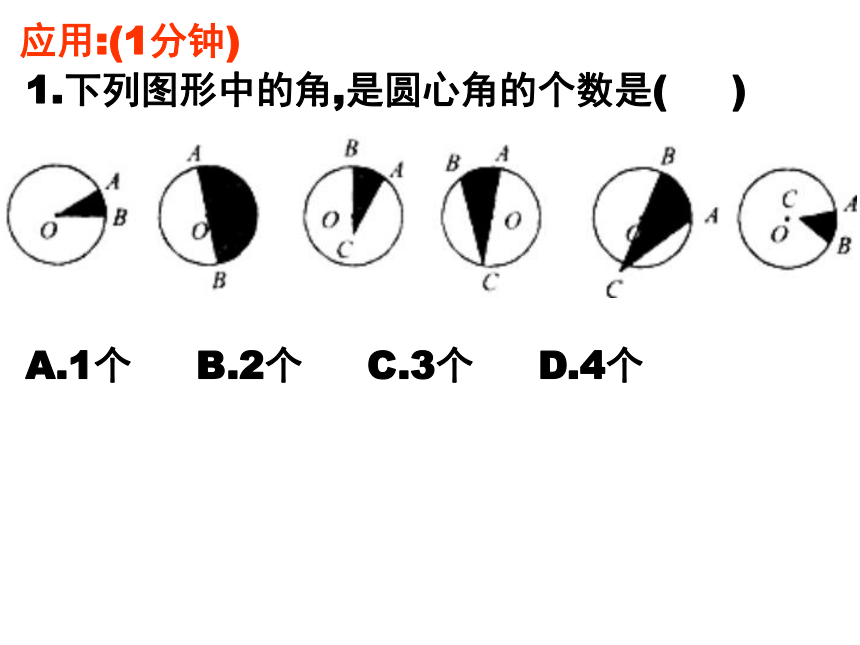
1.下列图形中的角,是圆心角的个数是( )
A.1个 B.2个 C.3个 D.4个
应用:(1分钟)
1°圆心角
1°弧
C
D
n°圆心角
n°弧
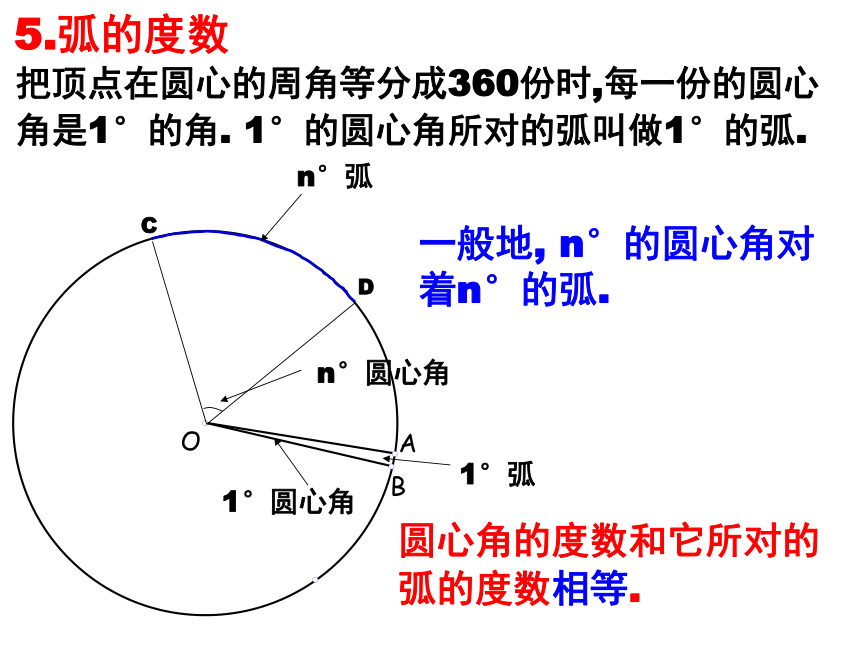
把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. 1°的圆心角所对的弧叫做1°的弧.
圆心角的度数和它所对的弧的度数相等.
一般地, n°的圆心角对着n°的弧.
5.弧的度数
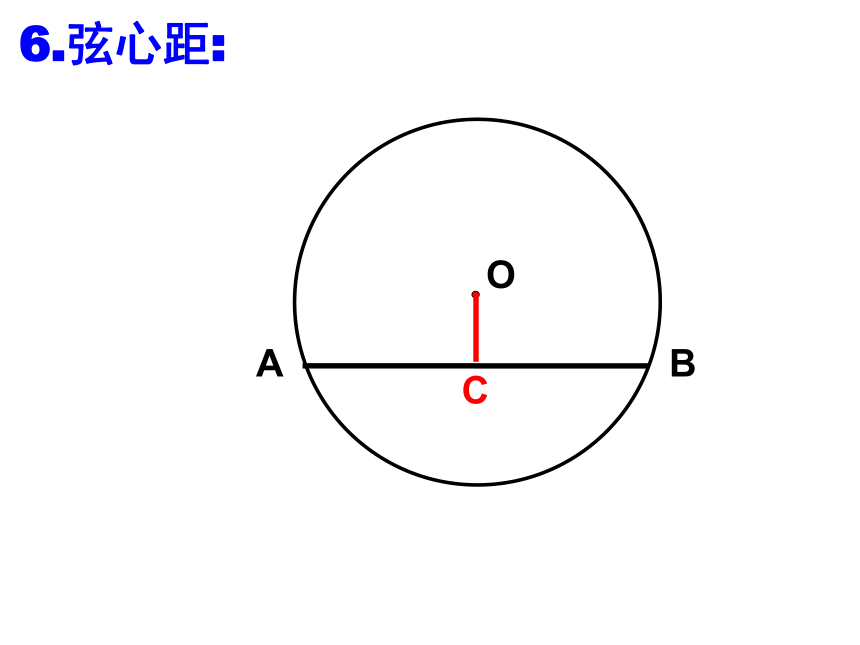
6.弦心距:
O
B
A
C
·
O
A
B
·
O
A
B
A′
B′
A′
B′
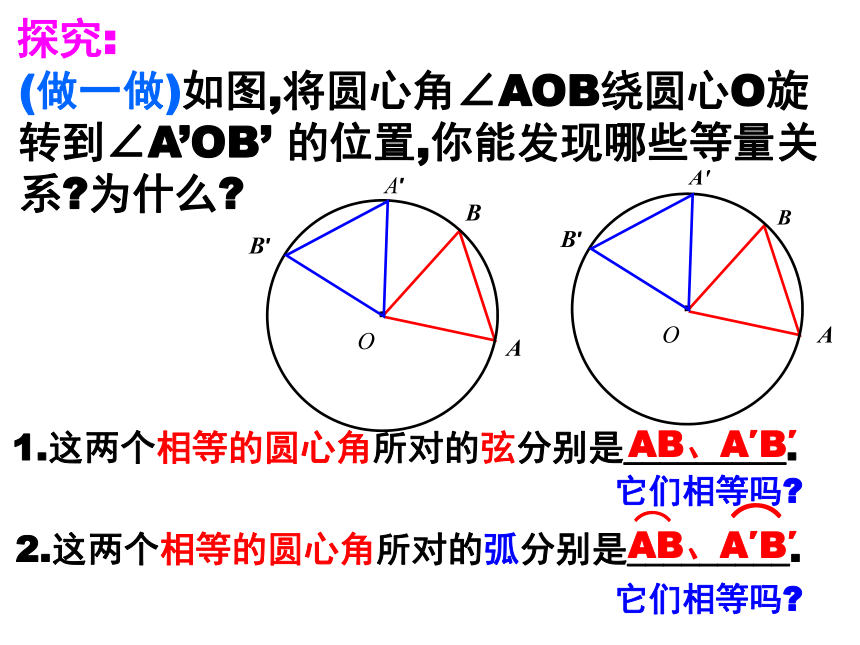
(做一做)如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’ 的位置,你能发现哪些等量关系?为什么?
探究:
1.这两个相等的圆心角所对的弦分别是_________.
2.这两个相等的圆心角所对的弧分别是_________.
AB、A′B′
AB、A′B′
︵
︵
它们相等吗?
它们相等吗?
α
A
B
A1
B1
α
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
∵∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
O
几何语言:
E
E1
OE=OE1
(不能直接用,需证明)
思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?
相等
E
E1
圆心角、弧、弦之间的关系
C
A
F
B
E
O
D
C
C′
在同圆或等圆中
两个圆心角
两条弧
两条弦
两条弦的弦心距
有一组量相等
它们所对应的其余各组量都分别相等
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等.
所对的弦心距相等.
?
反例:
1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等
B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等
D.以上答案都不对
D
自学检测1:(8分钟)
2.(2019?厦门)如图,在⊙O中,AB= AC,∠A=30°,则∠B= .
3.如图,已知:AB是⊙O的直径,C、D是BE上的三等分点,∠AOE=60°,则∠COB= .
4.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
若弧AC的度数为100°,则∠AOE=______.
例:如图,AB,DE是⊙O的直径,C是⊙O上一点, 且AD=CE,BE与CE的大小有什么关系?为什么?
自学指导2:(4分钟)
认真阅读P71-72的例2,注意: 1.解题方法解题格式; 2.圆心角、弧、弦间的关系的应用.
仿例题,做习题:(3分钟)
1.完成P72的知识技能-1T;
?
?
自学检测2:(10分钟)
小结:以圆为背景,利用圆的性质寻找条件 证全等或相似.
2.完成P73的数学理解-3T;
C
D
变式:如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD、BC于E、F,延长BA交⊙A于G,求证:GE=EF.
3.完成P72的随堂练习-3T;
1.如图,量角器边缘上有P、Q两点,它们表示的读数分别为60°,30°,已知直径AB=4 ,连接PB交OQ于M,则QM的长为 .
当谈训练:(10分钟)
2.如图,⊙O中弦AB⊥AC,OD⊥AB,OE⊥AC. 若AB=AC,则四边形OEAD的形状是 ;
3.如图,AB是⊙O的直径, AC=CD,
(1)求证:△AOC是等边三角形;
(2)求证:OC∥BD.
∠COD=60°.
4.如图,已知AB是⊙O的直径,M、N分别是AO和BO的中点,CM⊥AB,DN⊥AB, 求证:AC=BD.
学习目标:(1分钟)
1.理解圆的对称性; 2.掌握圆心角、弧、弦、弦心距间的关系,并能用其解题.
认真阅读P70-71例题前的内容,并思考:
1.圆是轴对称图形,对称轴是 ,有 __条对称轴;
2.圆是中心对称图形吗?对称中心是______;
3.理解圆的旋转不变性; 4.理解:圆心角、弧、弦、弦心距间的关系.
自学指导1:(4分钟)
1.圆是轴对称图形吗?
2.如果是,它的对称轴是什么?你能找到多少条对称轴?
●O
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
3.圆是中心对称图形吗?
圆是中心对称图形.
对称中心为圆心
点拨:
圆绕圆心旋转任意角度与原图形重合.
4.圆心角:
顶点在圆心,且与圆相交所形成的角,叫做圆心角.
1.下列图形中的角,是圆心角的个数是( )
A.1个 B.2个 C.3个 D.4个
应用:(1分钟)
1°圆心角
1°弧
C
D
n°圆心角
n°弧
把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角. 1°的圆心角所对的弧叫做1°的弧.
圆心角的度数和它所对的弧的度数相等.
一般地, n°的圆心角对着n°的弧.
5.弧的度数
6.弦心距:
O
B
A
C
·
O
A
B
·
O
A
B
A′
B′
A′
B′
(做一做)如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’ 的位置,你能发现哪些等量关系?为什么?
探究:
1.这两个相等的圆心角所对的弦分别是_________.
2.这两个相等的圆心角所对的弧分别是_________.
AB、A′B′
AB、A′B′
︵
︵
它们相等吗?
它们相等吗?
α
A
B
A1
B1
α
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
∵∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
O
几何语言:
E
E1
OE=OE1
(不能直接用,需证明)
思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?
相等
E
E1
圆心角、弧、弦之间的关系
C
A
F
B
E
O
D
C
C′
在同圆或等圆中
两个圆心角
两条弧
两条弦
两条弦的弦心距
有一组量相等
它们所对应的其余各组量都分别相等
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等.
所对的弦心距相等.
?
反例:
1.如果两条弦相等,那么( )
A.这两条弦所对的弧相等
B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等
D.以上答案都不对
D
自学检测1:(8分钟)
2.(2019?厦门)如图,在⊙O中,AB= AC,∠A=30°,则∠B= .
3.如图,已知:AB是⊙O的直径,C、D是BE上的三等分点,∠AOE=60°,则∠COB= .
4.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
若弧AC的度数为100°,则∠AOE=______.
例:如图,AB,DE是⊙O的直径,C是⊙O上一点, 且AD=CE,BE与CE的大小有什么关系?为什么?
自学指导2:(4分钟)
认真阅读P71-72的例2,注意: 1.解题方法解题格式; 2.圆心角、弧、弦间的关系的应用.
仿例题,做习题:(3分钟)
1.完成P72的知识技能-1T;
?
?
自学检测2:(10分钟)
小结:以圆为背景,利用圆的性质寻找条件 证全等或相似.
2.完成P73的数学理解-3T;
C
D
变式:如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD、BC于E、F,延长BA交⊙A于G,求证:GE=EF.
3.完成P72的随堂练习-3T;
1.如图,量角器边缘上有P、Q两点,它们表示的读数分别为60°,30°,已知直径AB=4 ,连接PB交OQ于M,则QM的长为 .
当谈训练:(10分钟)
2.如图,⊙O中弦AB⊥AC,OD⊥AB,OE⊥AC. 若AB=AC,则四边形OEAD的形状是 ;
3.如图,AB是⊙O的直径, AC=CD,
(1)求证:△AOC是等边三角形;
(2)求证:OC∥BD.
∠COD=60°.
4.如图,已知AB是⊙O的直径,M、N分别是AO和BO的中点,CM⊥AB,DN⊥AB, 求证:AC=BD.
