2020-2021学年北师大版初中数学八年级下册6.4节多边形的内角与外角和同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版初中数学八年级下册6.4节多边形的内角与外角和同步练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览

文档简介
北师大版初中数学八年级下册第六章平行四边形第4节多边形的内角与外角和同步练习
一、单选题
1.如果一个多边形的每个内角都为150°,那么这个多边形的边数是(???
)
A.?6?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?18
2.一个n边形的内角和比外角和多540°,则n等于(??
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3.如图,已知
中,
,则
(??
).
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
4.一个多边形内角和是720?,则这个多边形的对角线条数为(???
)
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
5.利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点
为旋转中心,顺时针(或逆时针)旋转角度
,依次旋转五次而组成,则旋转角
的值不可能是(
??)
A.?36°?????????????????????????????????????B.?72°?????????????????????????????????????C.?144°?????????????????????????????????????D.?216°
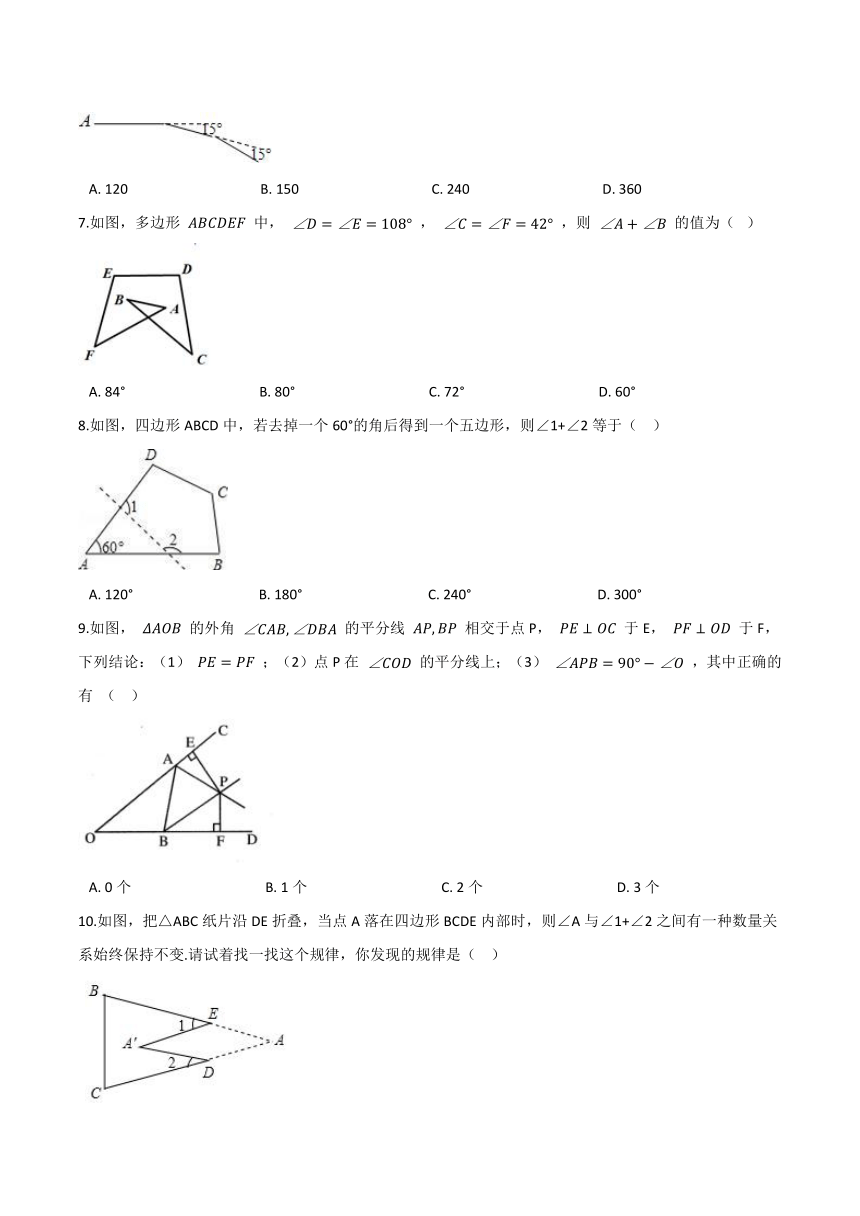
6.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,这样一直走下去,他第一次回到出发点A时,一共走了米数是(??
)
A.?120??????????????????????????????????????B.?150??????????????????????????????????????C.?240??????????????????????????????????????D.?360
7.如图,多边形
中,
,
,则
的值为(?
)
A.?84°???????????????????????????????????????B.?80°???????????????????????????????????????C.?72°???????????????????????????????????????D.?60°
8.如图,四边形ABCD中,若去掉一个60°的角后得到一个五边形,则∠1+∠2等于(??
)
A.?120°????????????????????????????????????B.?180°????????????????????????????????????C.?240°????????????????????????????????????D.?300°
9.如图,
的外角
的平分线
相交于点P,
于E,
于F,下列结论:(1)
;(2)点P在
的平分线上;(3)
,其中正确的有
(??
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是(??
)
A.?∠A=∠1+∠2???????????????B.?2∠A=∠1+∠2???????????????C.?3∠A=2∠1+∠2???????????????D.?3∠A=2(∠1+∠2)
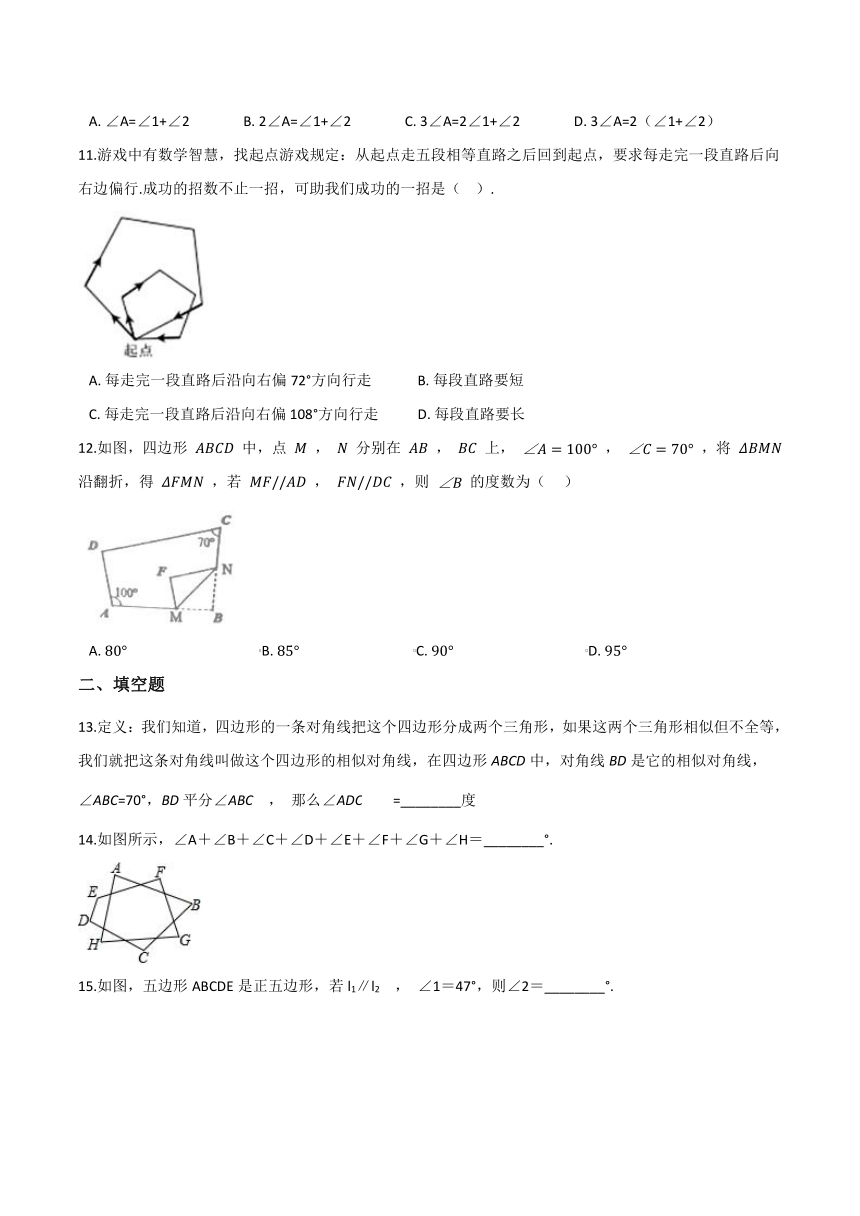
11.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是(??
).
A.?每走完一段直路后沿向右偏72°方向行走?????????????B.?每段直路要短
C.?每走完一段直路后沿向右偏108°方向行走???????????D.?每段直路要长
12.如图,四边形
中,点
,
分别在
,
上,
,
,将
沿翻折,得
,若
,
,则
的度数为(???
)
A.?
????????????????????????????????????B.??????????????????????????????????C.?
????????????????????????????????????D.?
二、填空题
13.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC
,
那么∠ADC=________度
14.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=________°.
15.如图,五边形ABCDE是正五边形,若l1∥l2
,
∠1=47°,则∠2=________°.
16.如图1,作
∠
BPC平分线的反向延长线PA,以
∠
APB,∠APC,∠BPC为内角可以分别作三个边长相等的正多边形.
例如:若∠BPC=90°,则∠APB=∠APC=135°,图2就是一个符合要求的图形.
在所有符合要求的图形中,∠BPC的度数是________.(∠BPC=90°除外)
17.如图,直线
,等边△ABC的顶点C在直线
上,若边AB与直线
的夹角
,则边AC与直线
的夹角∠2=________
.
18.如图,已知
,点D、C分别是EM、BN上的点,连接BD、CE交于点F
,
满足
,
,过点F作
交BN于点G
,
若
,则
________
.
三、解答题
19.如图,一个三角形的纸片ABC
,
其中∠A=∠C
.
①把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕.说明BC//DF;________
②把△ABC纸片沿DE折叠,当点A落在四边形BCED内时(如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;________
③当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是________.(直接写出结论)
20.如图,求
∠A+∠B+∠C+∠D+∠E+∠F的大小.
21.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
参考答案
1.
C
2.
C
3.
B
4.
C
5.
A
6.
C
7.
D
8.
C
9.
C
10.
B
11.
A
12.
D
13.
145
14.
720°
15.
119
16.
60°、120°、144°
17.
100
18.
36
19.
解:根据折叠的性质得:∠DFE=∠A,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
;解:2∠C=∠1+∠2,理由如下:
∵四边形的内角和等于360°,
∴∠A+∠A′+∠ADA′+∠AEA′=360°.
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2.
又∵∠A=∠A′,
∴2∠A=∠1+∠2,
∵∠A=∠C,
∴2∠C=∠1+∠2;
;2∠C=∠2?∠1
20.解:连结AD,如图,
在△EFG中,∠E+∠F+∠EGF=180°,
在△ADG中,∠1+∠2+∠AGD=180°,
∵∠EGF=∠AGD,
∴∠E+∠F=∠1+∠2,
∴∠A+
∠B+
∠C+
∠D+
∠E+∠F,
=∠BAF+∠B+
∠C
+∠CDE+
∠
1+
∠
2,
=∠BAD+
∠B+
∠C
+∠CDA,
=360°.
21.
解:∵在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠B,DF平分∠D,
∴∠ABE=∠EBC,∠ADF=∠FDC,
∴∠EBC+∠FDC=90°,
∵∠C=90°,
∴∠DFC+∠FDC=90°,
∴∠EBF=∠DFC,
∴BE∥DF
一、单选题
1.如果一个多边形的每个内角都为150°,那么这个多边形的边数是(???
)
A.?6?????????????????????????????????????????B.?11?????????????????????????????????????????C.?12?????????????????????????????????????????D.?18
2.一个n边形的内角和比外角和多540°,则n等于(??
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3.如图,已知
中,
,则
(??
).
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
4.一个多边形内角和是720?,则这个多边形的对角线条数为(???
)
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
5.利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点
为旋转中心,顺时针(或逆时针)旋转角度
,依次旋转五次而组成,则旋转角
的值不可能是(
??)
A.?36°?????????????????????????????????????B.?72°?????????????????????????????????????C.?144°?????????????????????????????????????D.?216°
6.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,这样一直走下去,他第一次回到出发点A时,一共走了米数是(??
)
A.?120??????????????????????????????????????B.?150??????????????????????????????????????C.?240??????????????????????????????????????D.?360
7.如图,多边形
中,
,
,则
的值为(?
)
A.?84°???????????????????????????????????????B.?80°???????????????????????????????????????C.?72°???????????????????????????????????????D.?60°
8.如图,四边形ABCD中,若去掉一个60°的角后得到一个五边形,则∠1+∠2等于(??
)
A.?120°????????????????????????????????????B.?180°????????????????????????????????????C.?240°????????????????????????????????????D.?300°
9.如图,
的外角
的平分线
相交于点P,
于E,
于F,下列结论:(1)
;(2)点P在
的平分线上;(3)
,其中正确的有
(??
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是(??
)
A.?∠A=∠1+∠2???????????????B.?2∠A=∠1+∠2???????????????C.?3∠A=2∠1+∠2???????????????D.?3∠A=2(∠1+∠2)
11.游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是(??
).
A.?每走完一段直路后沿向右偏72°方向行走?????????????B.?每段直路要短
C.?每走完一段直路后沿向右偏108°方向行走???????????D.?每段直路要长
12.如图,四边形
中,点
,
分别在
,
上,
,
,将
沿翻折,得
,若
,
,则
的度数为(???
)
A.?
????????????????????????????????????B.??????????????????????????????????C.?
????????????????????????????????????D.?
二、填空题
13.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC
,
那么∠ADC=________度
14.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=________°.
15.如图,五边形ABCDE是正五边形,若l1∥l2
,
∠1=47°,则∠2=________°.
16.如图1,作
∠
BPC平分线的反向延长线PA,以
∠
APB,∠APC,∠BPC为内角可以分别作三个边长相等的正多边形.
例如:若∠BPC=90°,则∠APB=∠APC=135°,图2就是一个符合要求的图形.
在所有符合要求的图形中,∠BPC的度数是________.(∠BPC=90°除外)
17.如图,直线
,等边△ABC的顶点C在直线
上,若边AB与直线
的夹角
,则边AC与直线
的夹角∠2=________
.
18.如图,已知
,点D、C分别是EM、BN上的点,连接BD、CE交于点F
,
满足
,
,过点F作
交BN于点G
,
若
,则
________
.
三、解答题
19.如图,一个三角形的纸片ABC
,
其中∠A=∠C
.
①把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕.说明BC//DF;________
②把△ABC纸片沿DE折叠,当点A落在四边形BCED内时(如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;________
③当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是________.(直接写出结论)
20.如图,求
∠A+∠B+∠C+∠D+∠E+∠F的大小.
21.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
参考答案
1.
C
2.
C
3.
B
4.
C
5.
A
6.
C
7.
D
8.
C
9.
C
10.
B
11.
A
12.
D
13.
145
14.
720°
15.
119
16.
60°、120°、144°
17.
100
18.
36
19.
解:根据折叠的性质得:∠DFE=∠A,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
;解:2∠C=∠1+∠2,理由如下:
∵四边形的内角和等于360°,
∴∠A+∠A′+∠ADA′+∠AEA′=360°.
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2.
又∵∠A=∠A′,
∴2∠A=∠1+∠2,
∵∠A=∠C,
∴2∠C=∠1+∠2;
;2∠C=∠2?∠1
20.解:连结AD,如图,
在△EFG中,∠E+∠F+∠EGF=180°,
在△ADG中,∠1+∠2+∠AGD=180°,
∵∠EGF=∠AGD,
∴∠E+∠F=∠1+∠2,
∴∠A+
∠B+
∠C+
∠D+
∠E+∠F,
=∠BAF+∠B+
∠C
+∠CDE+
∠
1+
∠
2,
=∠BAD+
∠B+
∠C
+∠CDA,
=360°.
21.
解:∵在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠B,DF平分∠D,
∴∠ABE=∠EBC,∠ADF=∠FDC,
∴∠EBC+∠FDC=90°,
∵∠C=90°,
∴∠DFC+∠FDC=90°,
∴∠EBF=∠DFC,
∴BE∥DF
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
