2020-2021学年北师大版初中数学八年级下册3.2节图形的旋转同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版初中数学八年级下册3.2节图形的旋转同步练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 10:59:33 | ||
图片预览

文档简介
北师大版初中数学八年级下册第三章图形的平移与旋转第2节图形的旋转同步练习
一、单选题
1.如图,是国旗中的一颗五角星图案,绕着它的中心旋转,要使旋转后的五角星能与自身重合,则旋转角的度数至少为(??
).
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?72°
2.经过以下变化后所得到的三角形不能和
全等的是(??
)
A.?????????????B.?????????????C.?????????????D.?
3.如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是(
??)
A.?????????????????????B.?BC=DE????????????????????C.?BC//AE????????????????????D.?AC平分
4.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=(??
)
A.?1.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?4??????????????????????????????????????????D.?5
5.在平面直角坐标系
中,将点
绕原点O逆时针旋转180°,得到的对应点的坐标是(???
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
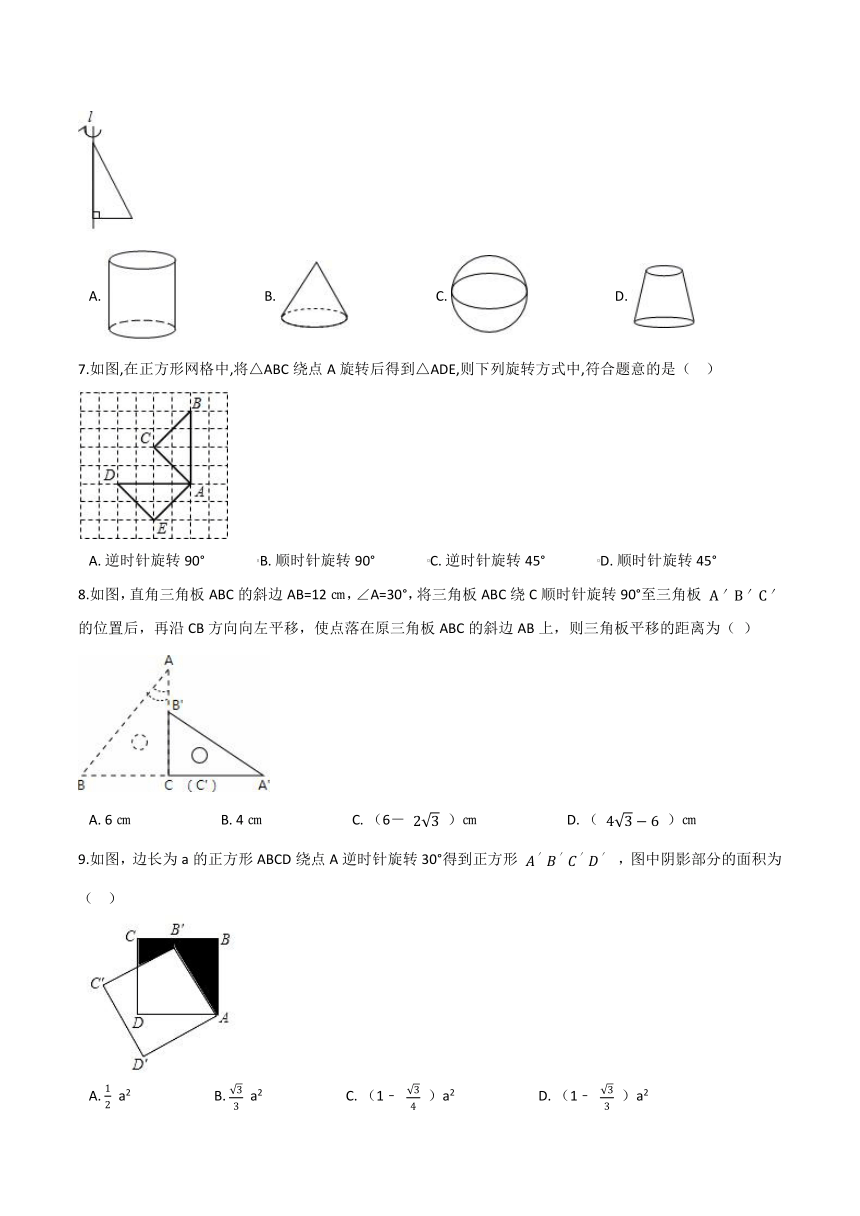
6.如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
7.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是(??
)
A.?逆时针旋转90°???????????????B.?顺时针旋转90°???????????????C.?逆时针旋转45°???????????????D.?顺时针旋转45°
8.如图,直角三角板ABC的斜边AB=12㎝,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板
的位置后,再沿CB方向向左平移,使点落在原三角板ABC的斜边AB上,则三角板平移的距离为(
)
A.?6㎝??????????????????????????B.?4㎝??????????????????????????C.?(6-
)㎝??????????????????????????D.?(
)㎝
9.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形
,图中阴影部分的面积为(??
)
A.?
a2????????????????????????B.?
a2????????????????????????C.?(1﹣
)a2????????????????????????D.?(1﹣
)a2
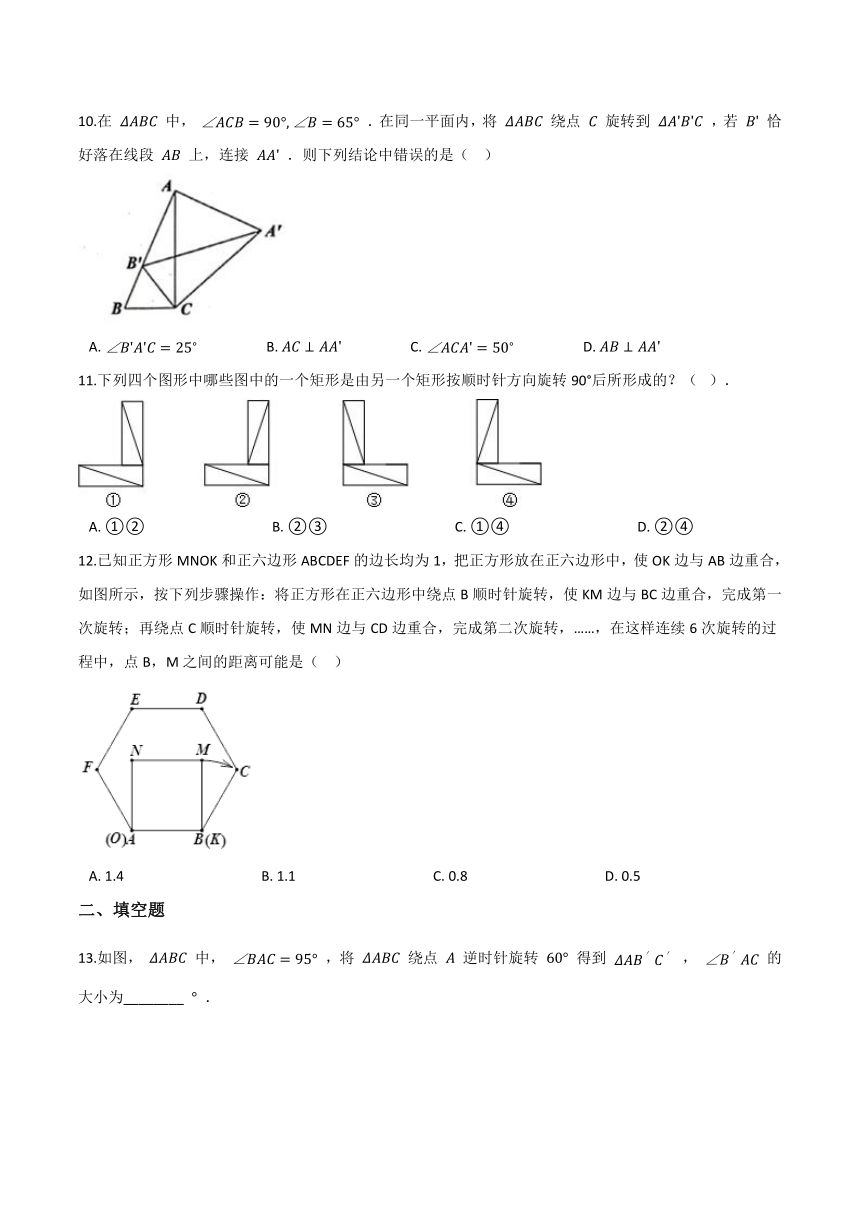
10.在
中,
.在同一平面内,将
绕点
旋转到
,若
恰好落在线段
上,连接
.则下列结论中错误的是(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
11.下列四个图形中哪些图中的一个矩形是由另一个矩形按顺时针方向旋转90°后所形成的?(?
).
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
12.已知正方形MNOK和正六边形ABCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是(??
)
A.?1.4????????????????????????????????????????B.?1.1????????????????????????????????????????C.?0.8????????????????????????????????????????D.?0.5
二、填空题
13.如图,
中,
,将
绕点
逆时针旋转
得到
,
的大小为________
.
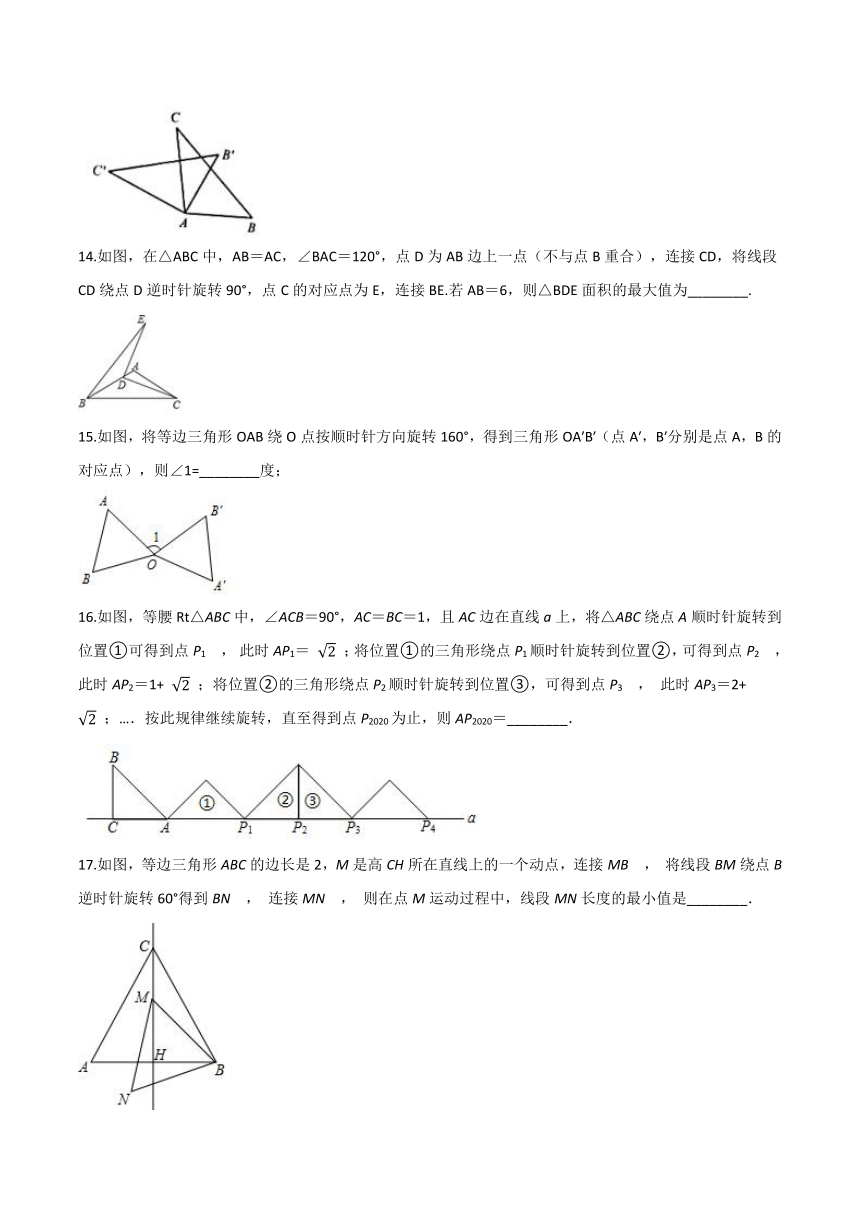
14.如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=6,则△BDE面积的最大值为________.
15.如图,将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA′B′(点A′,B′分别是点A,B的对应点),则∠1=________度;
16.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1
,
此时AP1=
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2
,
此时AP2=1+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3
,
此时AP3=2+
;….按此规律继续旋转,直至得到点P2020为止,则AP2020=________.
17.如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB
,
将线段BM绕点B逆时针旋转60°得到BN
,
连接MN
,
则在点M运动过程中,线段MN长度的最小值是________.
18.等边△ABC的边长为2,等边△DEF的边长为1,把△DEF放在△ABC中,使∠D与∠A重合,点E在AB边上,如图所示,此时点E是AB的中点,在△ABC内部将△DEF按照下列的方式旋转:绕点E顺时针旋转,使点F与点B重合,完成一次操作,此时点D是BC的中点,△DEF旋转了________°;再绕点D顺时针旋转,使点E与点C重合,完成第二次操作;…每次绕△DEF的某个顶点连续旋转下去,第11次操作完成时,CD=________.
三、解答题
19.己知,如图,点P是等边△ABC
内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点
处,求
的度数.
20.将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?
21.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
22.长江汛期即将来临,为r便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是3度/秒,灯B转动的速度是1度/秒.假定这一带长江两岸河堤是平行的,即PQ∥MN.如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,求∠BAC与∠BCD的比值,并说明理由。
参考答案
1.
D
2.
D
3.
C
4.
A
5.
B
6.
B
7.
A
8.
C
9.
D
10.
B
11.
D
12.
C
13.
35
14.
15.
100
16.
1346+674
17.
1.
18.
120;1
19.
解∶∵△APB≌AP'C,
∴∠AP'C=∠APB=112°,
且AP'=AP,∠BAP=∠CAP',
又∵∠BAP+∠PAC=60°,
∴∠CAP'+∠PAC=60°,
即∠PAP'=60°,
∴△PAP'是等边三角形,
∴∠PP'C=∠AP'C-∠AP'P=112°-60°=52°.
20.
(1)解:∵△BCN绕点C逆时针旋转90°得到△ACF,
∴CF=CN,∠ACF=∠BCN,
∵∠DCE=45°,
∴∠ACM+∠BCN=45°,
∴∠ACM+∠ACF=45°,
即∠MCF=45°,
∴∠MCF=∠MCN,
在△CMF和△CMN中,
,
∴△CMF≌△CMN(SAS)
(2)解:①∵△CMF≌△CMN,
∴FM=MN,
又∵∠CAF=∠B=45°,
∴∠FAM=∠CAF+∠BAC=45°+45°=90°,
∴AM2+AF2=FM2
,
∴AM2+BN2=MN2;
②如图,把△BCN绕点C逆时针旋转90°得到△ACF,
则AF=BN,CF=CN,∠BCN=∠ACF,
∵∠MCF=∠ACB-∠MCB-∠ACF=90°-(45°-∠BCN)-∠ACF=45°+∠BCN-∠ACF=45°,
∴∠MCF=∠MCN,
在△CMF和△CMN中,
,
∴△CMF≌△CMN(SAS),
∴FM=MN,
∵∠ABC=45°,
∴∠CAF=∠CBN=135°,
又∵∠BAC=45°,
∴∠FAM=∠CAF-∠BAC=135°-45°=90°,
∴AM2+AF2=FM2
,
∴AM2+BN2=MN2
.
21.解:∵菱形ABCD,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°﹣∠DCE,在△BCE和△DCF中,∵BC=CD,∠BCE=∠DCF,CE=CF,∴△BCE≌△DCF,∴∠F=∠E=86°
22.
解:设A灯转动时间为t秒,
∵∠CAN=180°﹣3t,
∴∠BAC=45°﹣(180°﹣3t)=3t﹣135°,
又∵PQ∥MN,
∴∠BCA=∠CBD+∠CAN=t+180°﹣3t=180°﹣2t,
而∠ACD=90°,
∴∠BCD=90°﹣∠BCA=90°﹣(180°﹣2t)=2t﹣90°,
即2∠BAC=3∠BCD
或者∠BAC=
∠BCD.
一、单选题
1.如图,是国旗中的一颗五角星图案,绕着它的中心旋转,要使旋转后的五角星能与自身重合,则旋转角的度数至少为(??
).
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?72°
2.经过以下变化后所得到的三角形不能和
全等的是(??
)
A.?????????????B.?????????????C.?????????????D.?
3.如图,将△ABC绕点A顺时针旋转到△ADE的位置,且点D恰好落在AC边上,则下列结论不一定成立的是(
??)
A.?????????????????????B.?BC=DE????????????????????C.?BC//AE????????????????????D.?AC平分
4.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=(??
)
A.?1.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?4??????????????????????????????????????????D.?5
5.在平面直角坐标系
中,将点
绕原点O逆时针旋转180°,得到的对应点的坐标是(???
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
6.如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
7.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是(??
)
A.?逆时针旋转90°???????????????B.?顺时针旋转90°???????????????C.?逆时针旋转45°???????????????D.?顺时针旋转45°
8.如图,直角三角板ABC的斜边AB=12㎝,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板
的位置后,再沿CB方向向左平移,使点落在原三角板ABC的斜边AB上,则三角板平移的距离为(
)
A.?6㎝??????????????????????????B.?4㎝??????????????????????????C.?(6-
)㎝??????????????????????????D.?(
)㎝
9.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形
,图中阴影部分的面积为(??
)
A.?
a2????????????????????????B.?
a2????????????????????????C.?(1﹣
)a2????????????????????????D.?(1﹣
)a2
10.在
中,
.在同一平面内,将
绕点
旋转到
,若
恰好落在线段
上,连接
.则下列结论中错误的是(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
11.下列四个图形中哪些图中的一个矩形是由另一个矩形按顺时针方向旋转90°后所形成的?(?
).
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
12.已知正方形MNOK和正六边形ABCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是(??
)
A.?1.4????????????????????????????????????????B.?1.1????????????????????????????????????????C.?0.8????????????????????????????????????????D.?0.5
二、填空题
13.如图,
中,
,将
绕点
逆时针旋转
得到
,
的大小为________
.
14.如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=6,则△BDE面积的最大值为________.
15.如图,将等边三角形OAB绕O点按顺时针方向旋转160°,得到三角形OA′B′(点A′,B′分别是点A,B的对应点),则∠1=________度;
16.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1
,
此时AP1=
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2
,
此时AP2=1+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3
,
此时AP3=2+
;….按此规律继续旋转,直至得到点P2020为止,则AP2020=________.
17.如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB
,
将线段BM绕点B逆时针旋转60°得到BN
,
连接MN
,
则在点M运动过程中,线段MN长度的最小值是________.
18.等边△ABC的边长为2,等边△DEF的边长为1,把△DEF放在△ABC中,使∠D与∠A重合,点E在AB边上,如图所示,此时点E是AB的中点,在△ABC内部将△DEF按照下列的方式旋转:绕点E顺时针旋转,使点F与点B重合,完成一次操作,此时点D是BC的中点,△DEF旋转了________°;再绕点D顺时针旋转,使点E与点C重合,完成第二次操作;…每次绕△DEF的某个顶点连续旋转下去,第11次操作完成时,CD=________.
三、解答题
19.己知,如图,点P是等边△ABC
内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点
处,求
的度数.
20.将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?
21.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
22.长江汛期即将来临,为r便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是3度/秒,灯B转动的速度是1度/秒.假定这一带长江两岸河堤是平行的,即PQ∥MN.如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,求∠BAC与∠BCD的比值,并说明理由。
参考答案
1.
D
2.
D
3.
C
4.
A
5.
B
6.
B
7.
A
8.
C
9.
D
10.
B
11.
D
12.
C
13.
35
14.
15.
100
16.
1346+674
17.
1.
18.
120;1
19.
解∶∵△APB≌AP'C,
∴∠AP'C=∠APB=112°,
且AP'=AP,∠BAP=∠CAP',
又∵∠BAP+∠PAC=60°,
∴∠CAP'+∠PAC=60°,
即∠PAP'=60°,
∴△PAP'是等边三角形,
∴∠PP'C=∠AP'C-∠AP'P=112°-60°=52°.
20.
(1)解:∵△BCN绕点C逆时针旋转90°得到△ACF,
∴CF=CN,∠ACF=∠BCN,
∵∠DCE=45°,
∴∠ACM+∠BCN=45°,
∴∠ACM+∠ACF=45°,
即∠MCF=45°,
∴∠MCF=∠MCN,
在△CMF和△CMN中,
,
∴△CMF≌△CMN(SAS)
(2)解:①∵△CMF≌△CMN,
∴FM=MN,
又∵∠CAF=∠B=45°,
∴∠FAM=∠CAF+∠BAC=45°+45°=90°,
∴AM2+AF2=FM2
,
∴AM2+BN2=MN2;
②如图,把△BCN绕点C逆时针旋转90°得到△ACF,
则AF=BN,CF=CN,∠BCN=∠ACF,
∵∠MCF=∠ACB-∠MCB-∠ACF=90°-(45°-∠BCN)-∠ACF=45°+∠BCN-∠ACF=45°,
∴∠MCF=∠MCN,
在△CMF和△CMN中,
,
∴△CMF≌△CMN(SAS),
∴FM=MN,
∵∠ABC=45°,
∴∠CAF=∠CBN=135°,
又∵∠BAC=45°,
∴∠FAM=∠CAF-∠BAC=135°-45°=90°,
∴AM2+AF2=FM2
,
∴AM2+BN2=MN2
.
21.解:∵菱形ABCD,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°﹣∠DCE,在△BCE和△DCF中,∵BC=CD,∠BCE=∠DCF,CE=CF,∴△BCE≌△DCF,∴∠F=∠E=86°
22.
解:设A灯转动时间为t秒,
∵∠CAN=180°﹣3t,
∴∠BAC=45°﹣(180°﹣3t)=3t﹣135°,
又∵PQ∥MN,
∴∠BCA=∠CBD+∠CAN=t+180°﹣3t=180°﹣2t,
而∠ACD=90°,
∴∠BCD=90°﹣∠BCA=90°﹣(180°﹣2t)=2t﹣90°,
即2∠BAC=3∠BCD
或者∠BAC=
∠BCD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
