2020-2021学年九年级数学人教版下册第二十九章投影与视图29.3节课题学习制作立体模型课后练习(word含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第二十九章投影与视图29.3节课题学习制作立体模型课后练习(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 16:51:38 | ||
图片预览

文档简介
人教版初中数学九年级下册第二十九章投影与视图29.3节课题学习制作立体模型课后练习
一、单选题
1.如图所示的表面展开图所对应的几何体是(??
)
A.?长方体?????????????????????????????????????B.?球?????????????????????????????????????C.?圆柱?????????????????????????????????????D.?圆锥
2.下列图形中是正方体表面展开图的是(??
)
A.?????????????????B.?????????????????C.?????????????????D.??
3.如图为正方体的一种平面展开图,各面都标有数字,则数字为
的面与其对面上的数字之积是(??
)
A.?-12?????????????????????????????????????????B.?0?????????????????????????????????????????C.?-8?????????????????????????????????????????D.?-10
4.把如图所示的纸片沿着虚线折叠,可以得到的几何体是(??
)
A.?三棱柱????????????????????????????????B.?四棱柱????????????????????????????????C.?三棱锥????????????????????????????????D.?四棱锥
5.下列图形中不可能拼成正方体的是(??
)
A.????????????????????B.????????????????????C.????????????????????D.?
6.制作一个底面直径6分米、长5分米的圆柱形通风管,至少要用(
????)平方分米的铁皮。
A.?62.8????????????????????????????????????B.?94.2????????????????????????????????????C.?188.4????????????????????????????????????D.?565.2
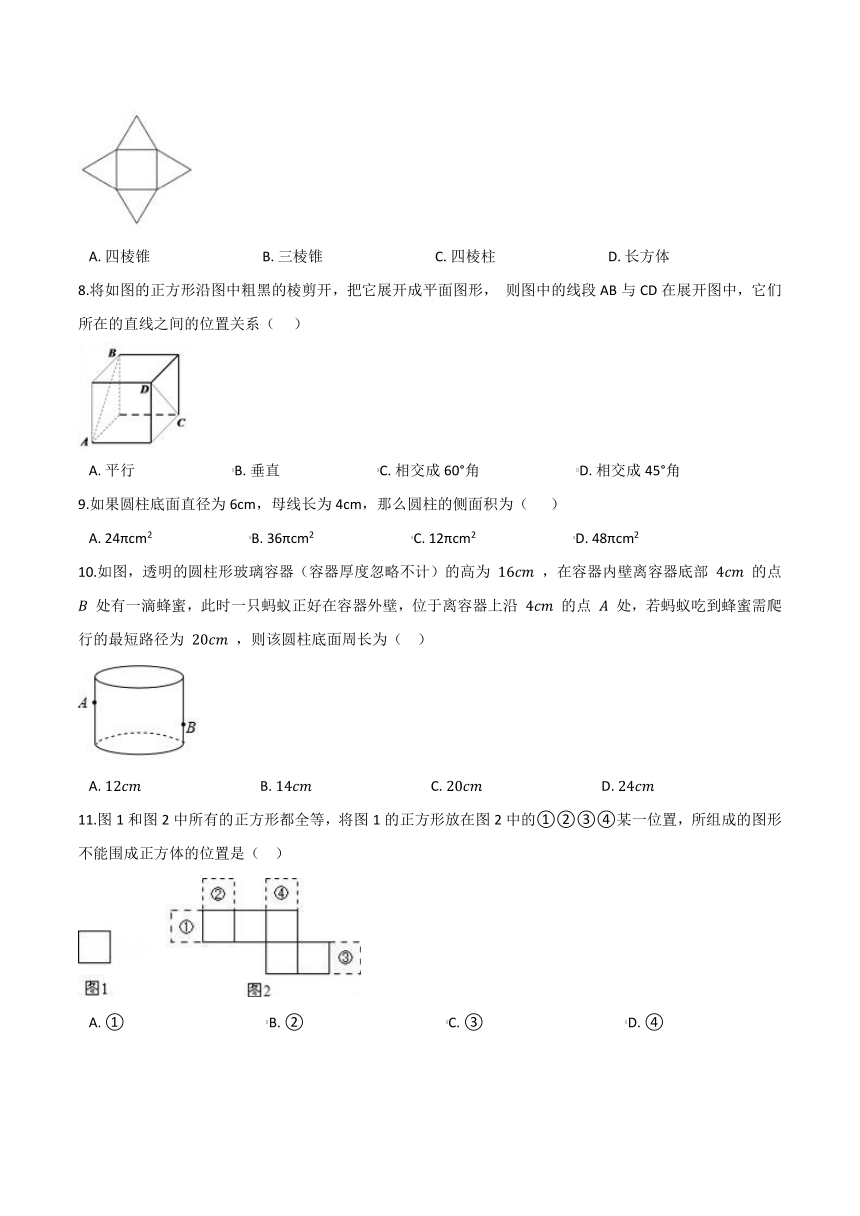
7.如图是某几何体的展开图,则该几何体是(???
)
A.?四棱锥????????????????????????????????B.?三棱锥????????????????????????????????C.?四棱柱????????????????????????????????D.?长方体
8.将如图的正方形沿图中粗黑的棱剪开,把它展开成平面图形,
则图中的线段AB与CD在展开图中,它们所在的直线之间的位置关系(???
)
A.?平行????????????????????????????B.?垂直????????????????????????????C.?相交成60°角????????????????????????????D.?相交成45°角
9.如果圆柱底面直径为6cm,母线长为4cm,那么圆柱的侧面积为(????
)
A.?24πcm2????????????????????????????B.?36πcm2????????????????????????????C.?12πcm2????????????????????????????D.?48πcm2
10.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为
,在容器内壁离容器底部
的点
处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿
的点
处,若蚂蚁吃到蜂蜜需爬行的最短路径为
,则该圆柱底面周长为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
11.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是(??
)
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
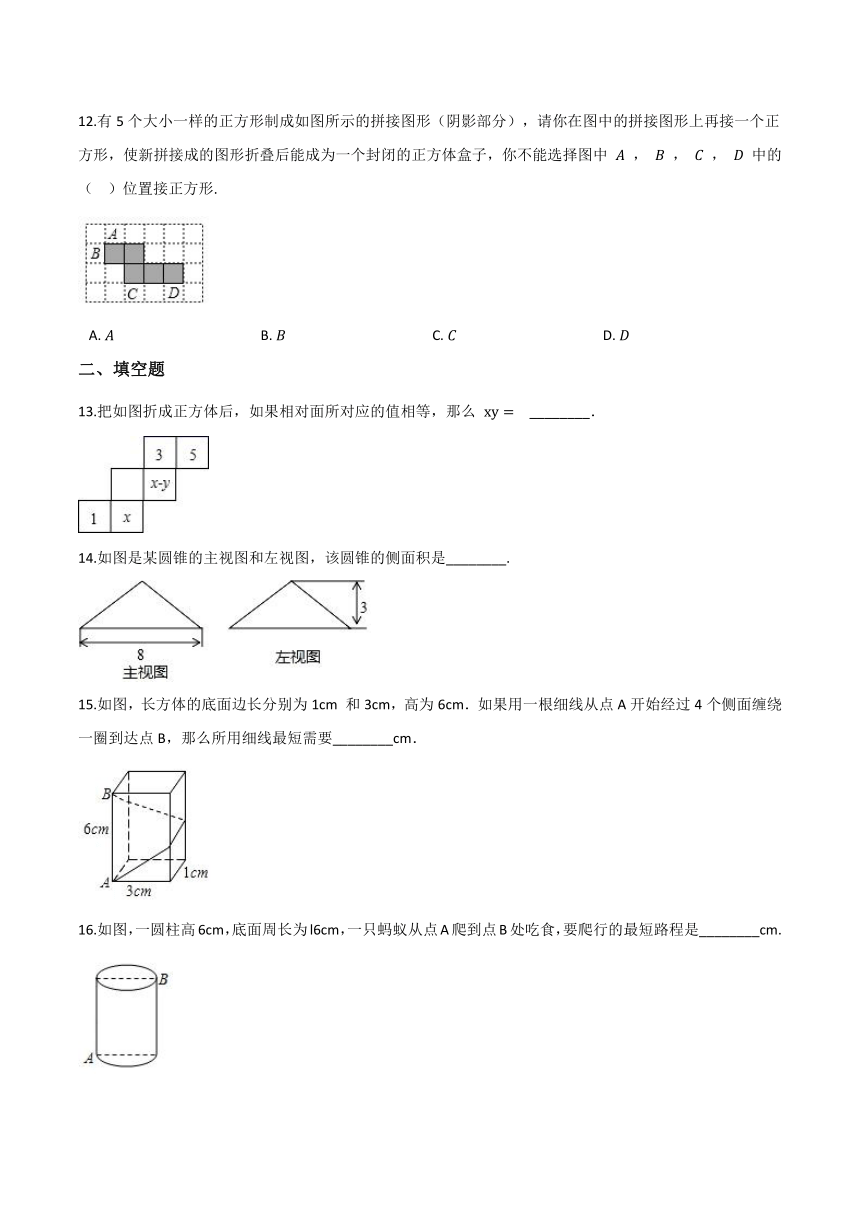
12.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中
,
,
,
中的(??
)位置接正方形.
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
13.把如图折成正方体后,如果相对面所对应的值相等,那么
________.
14.如图是某圆锥的主视图和左视图,该圆锥的侧面积是________.
15.如图,长方体的底面边长分别为1cm
和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要________cm.
16.如图,一圆柱高6cm,底面周长为l6cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是________cm.
17.如图,长方体中,
,
,
,一只蚂蚁从点A出发,以4m/秒的速度沿长方体表面爬行到点C',至少需要________
分钟.
18.如图,在一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为________.
三、解答题(共4题;共25分)
19.下图是长方体的表面展开图,将它折叠成一个长方体.
?(1)哪几个点与点
重合?
(2)若
,
,
,求这个长方体的表面积和体积.
20.某产品的形状是长方体,长为
,它的展开图如图所示,求长方体的体积.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱。
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
22.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
参考答案
1.
D
2.
D
3.
A
4.
A
5.
C
6.
B
7.
A
8.
A
9.
A
10.
D
11.
A
12.
A
13.
6
14.
20π
15.
10
16.
10
17.
18.
150cm
19.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由
,
,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
20.
解:设长方体的高为xcm,则长方形的宽为(14
2x)cm,根据题意可得:
14
2x+8+x+8=26,
解得:x=4,
所以长方体的高为4cm,宽为6cm,长为8cm,
长方形的体积为:8×6×4=192(cm3).
21.
解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
22.
解:(1)图甲折叠后底面和侧面都是长方形,所以是长方体;
图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.
(2)甲:f=6,e=12,v=8,f+v﹣e=2;
乙:f=6,e=10,v=6,f+v﹣e=2;
规律:顶点数+面数﹣棱数=2.
(3)设这个多面体的面数为x,则
x+x+8﹣50=2
解得x=22.
一、单选题
1.如图所示的表面展开图所对应的几何体是(??
)
A.?长方体?????????????????????????????????????B.?球?????????????????????????????????????C.?圆柱?????????????????????????????????????D.?圆锥
2.下列图形中是正方体表面展开图的是(??
)
A.?????????????????B.?????????????????C.?????????????????D.??
3.如图为正方体的一种平面展开图,各面都标有数字,则数字为
的面与其对面上的数字之积是(??
)
A.?-12?????????????????????????????????????????B.?0?????????????????????????????????????????C.?-8?????????????????????????????????????????D.?-10
4.把如图所示的纸片沿着虚线折叠,可以得到的几何体是(??
)
A.?三棱柱????????????????????????????????B.?四棱柱????????????????????????????????C.?三棱锥????????????????????????????????D.?四棱锥
5.下列图形中不可能拼成正方体的是(??
)
A.????????????????????B.????????????????????C.????????????????????D.?
6.制作一个底面直径6分米、长5分米的圆柱形通风管,至少要用(
????)平方分米的铁皮。
A.?62.8????????????????????????????????????B.?94.2????????????????????????????????????C.?188.4????????????????????????????????????D.?565.2
7.如图是某几何体的展开图,则该几何体是(???
)
A.?四棱锥????????????????????????????????B.?三棱锥????????????????????????????????C.?四棱柱????????????????????????????????D.?长方体
8.将如图的正方形沿图中粗黑的棱剪开,把它展开成平面图形,
则图中的线段AB与CD在展开图中,它们所在的直线之间的位置关系(???
)
A.?平行????????????????????????????B.?垂直????????????????????????????C.?相交成60°角????????????????????????????D.?相交成45°角
9.如果圆柱底面直径为6cm,母线长为4cm,那么圆柱的侧面积为(????
)
A.?24πcm2????????????????????????????B.?36πcm2????????????????????????????C.?12πcm2????????????????????????????D.?48πcm2
10.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为
,在容器内壁离容器底部
的点
处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿
的点
处,若蚂蚁吃到蜂蜜需爬行的最短路径为
,则该圆柱底面周长为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
11.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是(??
)
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
12.有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中
,
,
,
中的(??
)位置接正方形.
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
13.把如图折成正方体后,如果相对面所对应的值相等,那么
________.
14.如图是某圆锥的主视图和左视图,该圆锥的侧面积是________.
15.如图,长方体的底面边长分别为1cm
和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要________cm.
16.如图,一圆柱高6cm,底面周长为l6cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是________cm.
17.如图,长方体中,
,
,
,一只蚂蚁从点A出发,以4m/秒的速度沿长方体表面爬行到点C',至少需要________
分钟.
18.如图,在一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为________.
三、解答题(共4题;共25分)
19.下图是长方体的表面展开图,将它折叠成一个长方体.
?(1)哪几个点与点
重合?
(2)若
,
,
,求这个长方体的表面积和体积.
20.某产品的形状是长方体,长为
,它的展开图如图所示,求长方体的体积.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱。
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
22.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
参考答案
1.
D
2.
D
3.
A
4.
A
5.
C
6.
B
7.
A
8.
A
9.
A
10.
D
11.
A
12.
A
13.
6
14.
20π
15.
10
16.
10
17.
18.
150cm
19.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由
,
,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
20.
解:设长方体的高为xcm,则长方形的宽为(14
2x)cm,根据题意可得:
14
2x+8+x+8=26,
解得:x=4,
所以长方体的高为4cm,宽为6cm,长为8cm,
长方形的体积为:8×6×4=192(cm3).
21.
解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
22.
解:(1)图甲折叠后底面和侧面都是长方形,所以是长方体;
图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.
(2)甲:f=6,e=12,v=8,f+v﹣e=2;
乙:f=6,e=10,v=6,f+v﹣e=2;
规律:顶点数+面数﹣棱数=2.
(3)设这个多面体的面数为x,则
x+x+8﹣50=2
解得x=22.
