2020-2021学年人教版初中数学八年级下册第十七章勾股定理17.1节勾股定理课后练习(word含答案)
文档属性
| 名称 | 2020-2021学年人教版初中数学八年级下册第十七章勾股定理17.1节勾股定理课后练习(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 16:58:55 | ||
图片预览

文档简介
人教版初中数学八年级下册第十七章勾股定理17.1节勾股定理课后练习
一、单选题
1.以下列各组数据为三角形三边,能构成直角三角形的是(???
)
A.?4cm,8cm,7cm???????B.?3cm,5cm,2cm???????C.?2cm,2cm,4cm???????D.?13cm,12cm,5cm
2.在直角坐标系中,点P(﹣2,3)到原点的距离是(??
)
A.??????????????????????????????????????????B.?3?????????????????????????????????????????C.?2?????????????????????????????????????????D.?
3.在直角
中,
,如果
,
,那么
的长是(
??)
A.?2???????????????????????????????????????B.?5???????????????????????????????????????C.????????????????????????????????????????D.?5或
4.已知直角三角形的两条直角边的长分别为
和
,则斜边的长为(??
)
A.?3??????????????????????????????????????????B.?4??????????????????????????????????????????C.?5??????????????????????????????????????????D.?
5.平面直角坐标系中,点P(2,0)平移后对应的点为Q(5,4),则平移的距离为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?7
6.如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,
的长为半径画弧,交最上方的网格线于点D,则
的长为(???
)
A.??????????????????????????????????????B.?0.8?????????????????????????????????????C.??????????????????????????????????????D.?
7.如图,一棵高为16m的大树被台风刮断.若树在地面6m处折断,则树顶端落在离树底部(??
)处.
A.?5m??????????????????????????????????????B.?7m??????????????????????????????????????C.?7.5m??????????????????????????????????????D.?8m
8.如图,在
中,
,分别以B,C为圆心,大于BC的一半为半径作弧,两弧相交于D,E,作直线DE交AB,BC于点F,G,连接CF,若
,则
的长为(??
)
A.?3.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?2.5??????????????????????????????????????????D.?2
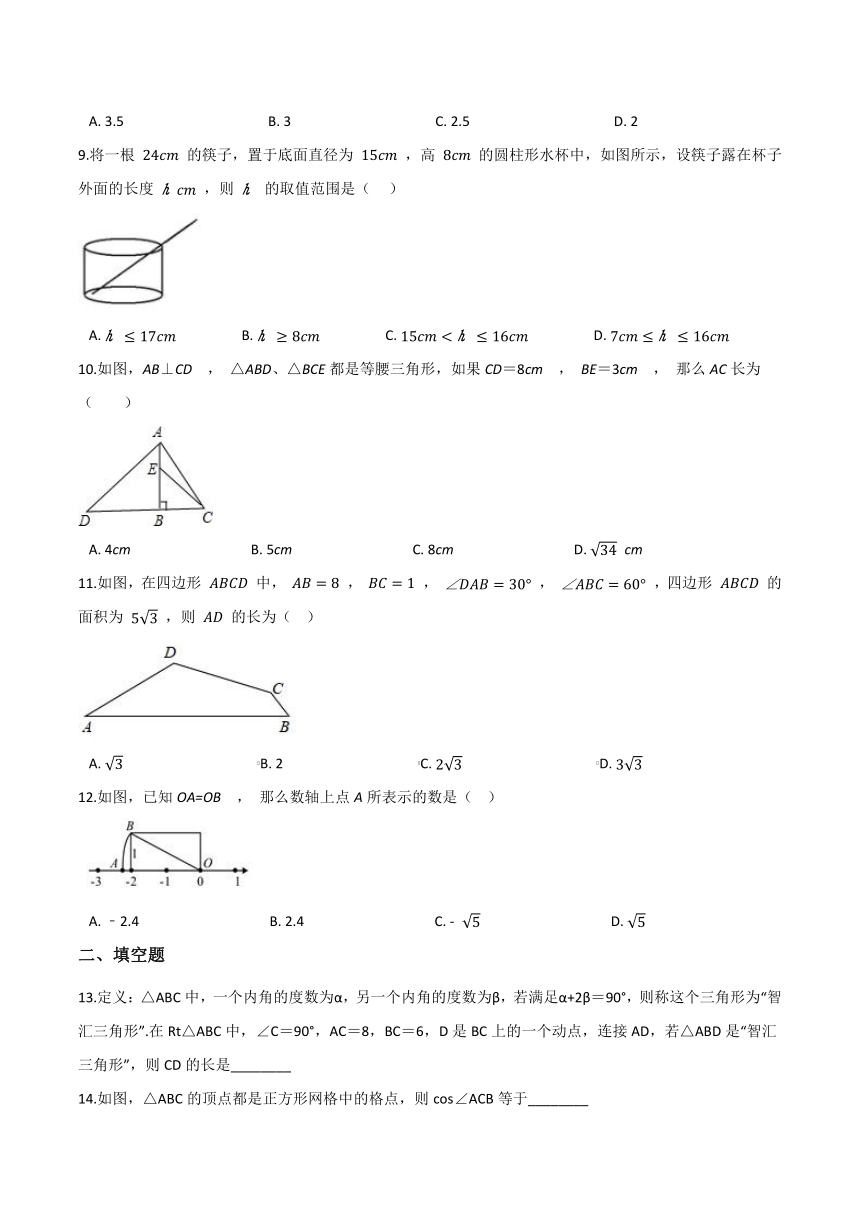
9.将一根
的筷子,置于底面直径为
,高
的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度
,则
的取值范围是(???
)
A.????????????????????B.????????????????????C.????????????????????D.?
10.如图,AB⊥CD
,
△ABD、△BCE都是等腰三角形,如果CD=8cm
,
BE=3cm
,
那么AC长为( )
A.?4cm???????????????????????????????????B.?5cm???????????????????????????????????C.?8cm???????????????????????????????????D.?
cm
11.如图,在四边形
中,
,
,
,
,四边形
的面积为
,则
的长为(??
)
A.????????????????????????????????????????B.?2???????????????????????????????????????C.????????????????????????????????????????D.?
12.如图,已知OA=OB
,
那么数轴上点A所表示的数是(??
)
A.?﹣2.4??????????????????????????????????????B.?2.4??????????????????????????????????????C.?-
??????????????????????????????????????D.?
二、填空题
13.定义:△ABC中,一个内角的度数为α,另一个内角的度数为β,若满足α+2β=90°,则称这个三角形为“智汇三角形”.在Rt△ABC中,∠C=90°,AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“智汇三角形”,则CD的长是________
14.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于________
15.如图,在边长为1的正方形网格中,两格点A
,
B之间的距离为d等于________.
16.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形
的边
在
轴上,
的中点是坐标原点
,固定点
,
,把正方形沿箭头方向推,使点
落在
轴正半轴上点
处,则点
的对应点
的坐标为________.
17.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________米.
18.如图,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,若图形中四边形ABCD和四边形EFGH都是正方形,△ABH,△BCG,△CDF,△DAE是四个全等的直角三角形,若EF=2,DE=6,则AB的长为________.
三、解答题
19.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km
,
B村庄到公路的距离BD=14km
,
测得C、D两点的距离为20km
,
现要在CD之间建一个服务区E
,
使得A、B两村庄到E服务区的距离相等,求CE的长.
20.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1
m,当他把绳子的下端拉开5
m后,发现下端刚好接触地面,求旗杆的高.
21.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于点A,CB⊥AB于点B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
22.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
参考答案
1.
D
2.
D
3.
C
4.
D
5.
C
6.
C
7.
D
8.
C
9.
D
10.
D
11.
C
12.
C
13.
14.
15.
16.
(2,
)
17.
7
18.
10
19.
解:设CE=x
km,则DE=(20﹣x)km.
在Rt△ACE中,由勾股定理得:AE2=AC2+CE2=82+x2
,
在Rt△BDE中,由勾股定理得:BE2=BD2+DE2=142+(20﹣x)2
,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2
,
解得:x=13.3,
所以CE=13.3km.
20.
解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2
,
解得,x=12.
答:旗杆的高度为12米.
21.
解:设AE=xkm,则BE=(20-x)km,
∵DE=CE,DA⊥AB,CB⊥AB,
∴AD2+AE2=BE2+BC2
,
即82+x2=(20-x)2+142
,
解得:x=13.3.
答:AE的长为13.3km.
22.
解:设旗杆的高度为x米,
根据勾股定理,得x2+92=(x+3)2
,
解得:x=12.
答:旗杆的高度为12米.
一、单选题
1.以下列各组数据为三角形三边,能构成直角三角形的是(???
)
A.?4cm,8cm,7cm???????B.?3cm,5cm,2cm???????C.?2cm,2cm,4cm???????D.?13cm,12cm,5cm
2.在直角坐标系中,点P(﹣2,3)到原点的距离是(??
)
A.??????????????????????????????????????????B.?3?????????????????????????????????????????C.?2?????????????????????????????????????????D.?
3.在直角
中,
,如果
,
,那么
的长是(
??)
A.?2???????????????????????????????????????B.?5???????????????????????????????????????C.????????????????????????????????????????D.?5或
4.已知直角三角形的两条直角边的长分别为
和
,则斜边的长为(??
)
A.?3??????????????????????????????????????????B.?4??????????????????????????????????????????C.?5??????????????????????????????????????????D.?
5.平面直角坐标系中,点P(2,0)平移后对应的点为Q(5,4),则平移的距离为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?7
6.如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,
的长为半径画弧,交最上方的网格线于点D,则
的长为(???
)
A.??????????????????????????????????????B.?0.8?????????????????????????????????????C.??????????????????????????????????????D.?
7.如图,一棵高为16m的大树被台风刮断.若树在地面6m处折断,则树顶端落在离树底部(??
)处.
A.?5m??????????????????????????????????????B.?7m??????????????????????????????????????C.?7.5m??????????????????????????????????????D.?8m
8.如图,在
中,
,分别以B,C为圆心,大于BC的一半为半径作弧,两弧相交于D,E,作直线DE交AB,BC于点F,G,连接CF,若
,则
的长为(??
)
A.?3.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?2.5??????????????????????????????????????????D.?2
9.将一根
的筷子,置于底面直径为
,高
的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度
,则
的取值范围是(???
)
A.????????????????????B.????????????????????C.????????????????????D.?
10.如图,AB⊥CD
,
△ABD、△BCE都是等腰三角形,如果CD=8cm
,
BE=3cm
,
那么AC长为( )
A.?4cm???????????????????????????????????B.?5cm???????????????????????????????????C.?8cm???????????????????????????????????D.?
cm
11.如图,在四边形
中,
,
,
,
,四边形
的面积为
,则
的长为(??
)
A.????????????????????????????????????????B.?2???????????????????????????????????????C.????????????????????????????????????????D.?
12.如图,已知OA=OB
,
那么数轴上点A所表示的数是(??
)
A.?﹣2.4??????????????????????????????????????B.?2.4??????????????????????????????????????C.?-
??????????????????????????????????????D.?
二、填空题
13.定义:△ABC中,一个内角的度数为α,另一个内角的度数为β,若满足α+2β=90°,则称这个三角形为“智汇三角形”.在Rt△ABC中,∠C=90°,AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“智汇三角形”,则CD的长是________
14.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于________
15.如图,在边长为1的正方形网格中,两格点A
,
B之间的距离为d等于________.
16.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形
的边
在
轴上,
的中点是坐标原点
,固定点
,
,把正方形沿箭头方向推,使点
落在
轴正半轴上点
处,则点
的对应点
的坐标为________.
17.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________米.
18.如图,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,若图形中四边形ABCD和四边形EFGH都是正方形,△ABH,△BCG,△CDF,△DAE是四个全等的直角三角形,若EF=2,DE=6,则AB的长为________.
三、解答题
19.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km
,
B村庄到公路的距离BD=14km
,
测得C、D两点的距离为20km
,
现要在CD之间建一个服务区E
,
使得A、B两村庄到E服务区的距离相等,求CE的长.
20.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了1
m,当他把绳子的下端拉开5
m后,发现下端刚好接触地面,求旗杆的高.
21.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于点A,CB⊥AB于点B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
22.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
参考答案
1.
D
2.
D
3.
C
4.
D
5.
C
6.
C
7.
D
8.
C
9.
D
10.
D
11.
C
12.
C
13.
14.
15.
16.
(2,
)
17.
7
18.
10
19.
解:设CE=x
km,则DE=(20﹣x)km.
在Rt△ACE中,由勾股定理得:AE2=AC2+CE2=82+x2
,
在Rt△BDE中,由勾股定理得:BE2=BD2+DE2=142+(20﹣x)2
,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2
,
解得:x=13.3,
所以CE=13.3km.
20.
解:设旗杆的高度为x米,则绳子的长度为(x+1)米,
根据勾股定理可得:x2+52=(x+1)2
,
解得,x=12.
答:旗杆的高度为12米.
21.
解:设AE=xkm,则BE=(20-x)km,
∵DE=CE,DA⊥AB,CB⊥AB,
∴AD2+AE2=BE2+BC2
,
即82+x2=(20-x)2+142
,
解得:x=13.3.
答:AE的长为13.3km.
22.
解:设旗杆的高度为x米,
根据勾股定理,得x2+92=(x+3)2
,
解得:x=12.
答:旗杆的高度为12米.
