北京市良乡中学2012届高三数学会考模拟试题(4)
文档属性
| 名称 | 北京市良乡中学2012届高三数学会考模拟试题(4) |  | |
| 格式 | zip | ||
| 文件大小 | 141.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-24 09:29:33 | ||
图片预览



文档简介
北京市良乡中学2012届高三数学会考模拟试题(4)
一、选择题(每题3分,共60分)
1、若,,则下列命题中成立的是( )
A. B. C. D.
2、不等式的解集是( )
A. B. C.或 D.
3、下列函数中,在上是减函数的是( )
4、在区间上随机取一个数,则≤1的概率为( )
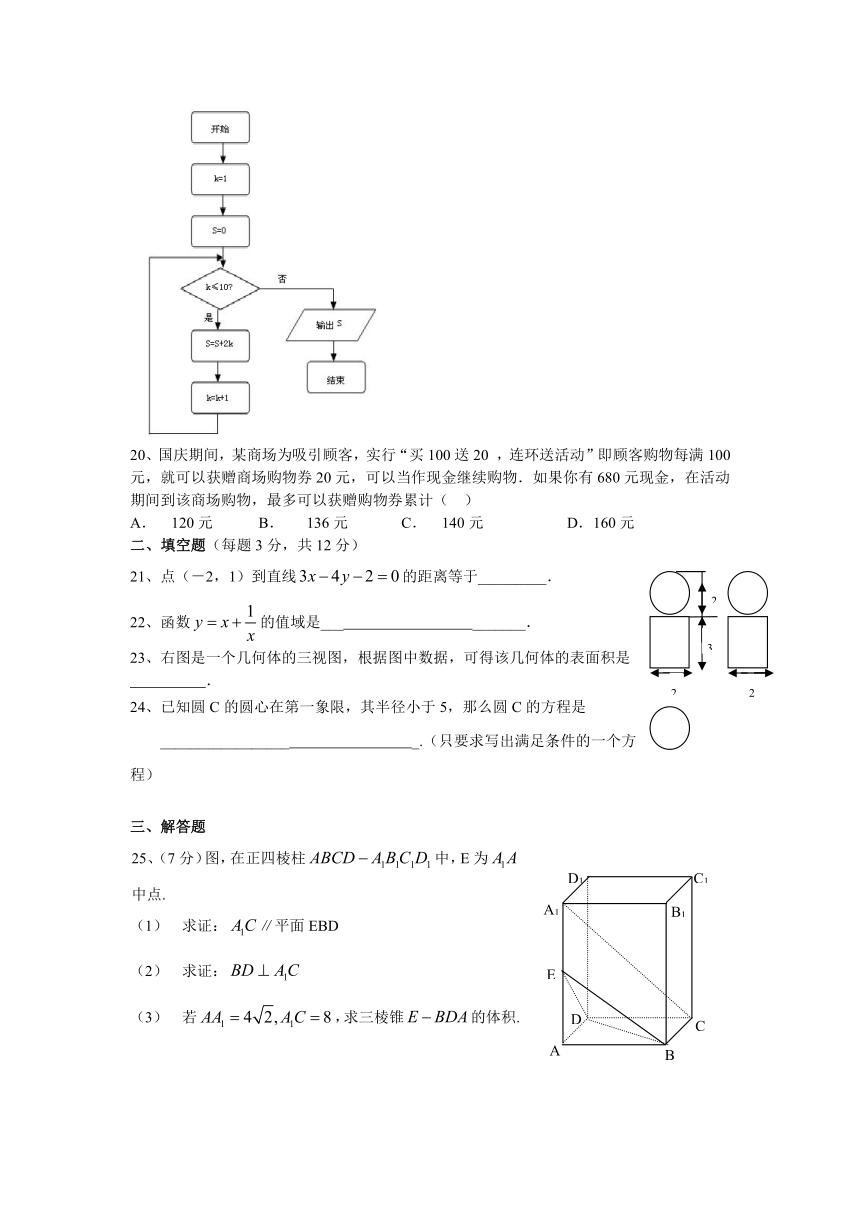
A. B. C. D.
5、函数的定义域是( )
A.或 B.且 C. D.
6、若,则cos2等于( )
A. B.- C.1 D.
7、已知角的终边经过点,则的值为( )
A. B. C. D.
8、函数的图像与 的图像( )
关于轴对称 关于轴对称
关于直线对称 关于直线对称
9、在中,,则角为 ( )
A. 30 B. C. D.
10、为了得到函数,的图象,只需将函数,的图象上所有的点( )
A. 向左平行移动个单位长度 B. 向右平行移动个单位长度
C. 向左平行移动个单位长度 D. 向右平行移动个单位长度
11、如果,,而且,那么的值是( )
A. 4 B. C. D.
12、在等差数列中,,,则等于( )
A. 19 B. 50 C. 100 D. 120
13、为改善生态环境,某城市对排污系统进行了整治。如果经过三年整治,城市排污量由原来每年排放125万吨降到27万吨,那么排污量平均每年降低的百分率是( )
40% 30% 20%
14、若、是异面直线,则一定存在两个平行平面、,使( )
A. , B. ,
C. , D. ,
15、从数字1,2,3,4,5中,随机抽取2个数字(不允许重复),则这两个数字之和为奇数的概率为( )
A. B. C. D.
16、圆截直线所得弦长为8,则的值为( )
A. 10 B.-68 C. 12 D. 10或-68
17、已知等比数列满足,则 ( )
A.64 B.81 C.128 D.243
18、已知点P(,)在不等式组表示的平面区域上运动,则的取值范围是( )
A.[-1,-1] B.[-1,1] C.[1,-1] D.[1,1]
19、如果执行右面的程序框图,那么输出的S等于( )
A.20 B. 90 C. 110 D. 132
20、国庆期间,某商场为吸引顾客,实行“买100送20 ,连环送活动”即顾客购物每满100元,就可以获赠商场购物券20元,可以当作现金继续购物.如果你有680元现金,在活动期间到该商场购物,最多可以获赠购物券累计( )
A. 120元 B. 136元 C. 140元 D.160元
二、填空题(每题3分,共12分)
21、点(-2,1)到直线的距离等于_________.
22、函数的值域是___ _______.
23、右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是
.
24、已知圆C的圆心在第一象限,其半径小于5,那么圆C的方程是
_________________ _.(只要求写出满足条件的一个方程)
三、解答题
25、(7分)图,在正四棱柱中,E为中点.
求证:∥平面EBD
求证:
若,求三棱锥的体积.
26、(7分)在中,已知内角A、B、C所对的边分别为a、b、c,向量,,且。
(I)求锐角B的大小;
(II)如果,求的面积的最大值。
27、(7分)设为数列的前项和,(为常数,).
(Ⅰ)若,求的值;
(Ⅱ)是否存在实数,使得数列是等差数列?若存在,求出的值;若不存在,说明理由;
(Ⅲ)当时,若数列满足,且,令. 求数列的前项和.
28.(7分)已知点,是轴上两点,且(B在C的左侧).设的外接圆的圆心为.
(Ⅰ)已知,试求直线的方程;
(Ⅱ)当圆与直线相切时,求圆的方程;
(Ⅲ)设,,,试求的最大值.
参考答案:
C2.D3.A4.B5.D6.B7.C8.B9.C10.C11.D12.C13.B14.A15.B16.D17.A18.B19.C20.D
21. 22. 23. 24. >?
25. 略。
26. (1)解:m∥n 2sinB(2cos2-1)=-cos2B
2sinBcosB=-cos2B tan2B=- ……4分
∵0<2B<π,∴2B=,∴锐角B= ……2分
(2)由tan2B=- B=或
①当B=时,已知b=2,由余弦定理,得:
4=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=2时等号成立) ……3分
∵△ABC的面积S△ABC= acsinB=ac≤
∴△ABC的面积最大值为 ……1分
②当B=时,已知b=2,由余弦定理,得:
4=a2+c2+ac≥2ac+ac=(2+)ac(当且仅当a=c=-时等号成立)
∴ac≤4(2-) ……1分
∵△ABC的面积S△ABC= acsinB=ac≤2-
∴△ABC的面积最大值为2- ……1分
27.解:(Ⅰ)因为,
所以,,.
……………………………………1分
由可知:.
所以,,.
因为,
所以.
所以或. ……………………………………3分
(Ⅱ)假设存在实数,使得数列是等差数列,则.
……………………………………4分
由(Ⅰ)可得:.
所以,即,矛盾.
所以不存在实数,使得数列是等差数列.
…………………………………6分
(Ⅲ)当时,.
所以,且.
所以,即.
所以,且.
所以,数列是以1为首项,2为公比的等比数列
所以. ………………………………8分
因为,且,
所以
.
当时,上式仍然成立.
所以 . ………………………………10分
因为,
所以.
………………………………11分
因为, …………………………………12分
所以
.
28.解:(1)设,则.
,,
由得,
解得:,
所以,直线的方程为
(2)设圆心为,半径为,则
解之得:,
所以,圆的方程为.
(3)设,则,
所以,,
等号当且仅当时取得.
2
2
2
3
A
B
C
D
E
B1
A1
C1
D1
一、选择题(每题3分,共60分)
1、若,,则下列命题中成立的是( )
A. B. C. D.
2、不等式的解集是( )
A. B. C.或 D.
3、下列函数中,在上是减函数的是( )
4、在区间上随机取一个数,则≤1的概率为( )
A. B. C. D.
5、函数的定义域是( )
A.或 B.且 C. D.
6、若,则cos2等于( )
A. B.- C.1 D.
7、已知角的终边经过点,则的值为( )
A. B. C. D.
8、函数的图像与 的图像( )
关于轴对称 关于轴对称
关于直线对称 关于直线对称
9、在中,,则角为 ( )
A. 30 B. C. D.
10、为了得到函数,的图象,只需将函数,的图象上所有的点( )
A. 向左平行移动个单位长度 B. 向右平行移动个单位长度
C. 向左平行移动个单位长度 D. 向右平行移动个单位长度
11、如果,,而且,那么的值是( )
A. 4 B. C. D.
12、在等差数列中,,,则等于( )
A. 19 B. 50 C. 100 D. 120
13、为改善生态环境,某城市对排污系统进行了整治。如果经过三年整治,城市排污量由原来每年排放125万吨降到27万吨,那么排污量平均每年降低的百分率是( )
40% 30% 20%
14、若、是异面直线,则一定存在两个平行平面、,使( )
A. , B. ,
C. , D. ,
15、从数字1,2,3,4,5中,随机抽取2个数字(不允许重复),则这两个数字之和为奇数的概率为( )
A. B. C. D.
16、圆截直线所得弦长为8,则的值为( )
A. 10 B.-68 C. 12 D. 10或-68
17、已知等比数列满足,则 ( )
A.64 B.81 C.128 D.243
18、已知点P(,)在不等式组表示的平面区域上运动,则的取值范围是( )
A.[-1,-1] B.[-1,1] C.[1,-1] D.[1,1]
19、如果执行右面的程序框图,那么输出的S等于( )
A.20 B. 90 C. 110 D. 132
20、国庆期间,某商场为吸引顾客,实行“买100送20 ,连环送活动”即顾客购物每满100元,就可以获赠商场购物券20元,可以当作现金继续购物.如果你有680元现金,在活动期间到该商场购物,最多可以获赠购物券累计( )
A. 120元 B. 136元 C. 140元 D.160元
二、填空题(每题3分,共12分)
21、点(-2,1)到直线的距离等于_________.
22、函数的值域是___ _______.
23、右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是
.
24、已知圆C的圆心在第一象限,其半径小于5,那么圆C的方程是
_________________ _.(只要求写出满足条件的一个方程)
三、解答题
25、(7分)图,在正四棱柱中,E为中点.
求证:∥平面EBD
求证:
若,求三棱锥的体积.
26、(7分)在中,已知内角A、B、C所对的边分别为a、b、c,向量,,且。
(I)求锐角B的大小;
(II)如果,求的面积的最大值。
27、(7分)设为数列的前项和,(为常数,).
(Ⅰ)若,求的值;
(Ⅱ)是否存在实数,使得数列是等差数列?若存在,求出的值;若不存在,说明理由;
(Ⅲ)当时,若数列满足,且,令. 求数列的前项和.
28.(7分)已知点,是轴上两点,且(B在C的左侧).设的外接圆的圆心为.
(Ⅰ)已知,试求直线的方程;
(Ⅱ)当圆与直线相切时,求圆的方程;
(Ⅲ)设,,,试求的最大值.
参考答案:
C2.D3.A4.B5.D6.B7.C8.B9.C10.C11.D12.C13.B14.A15.B16.D17.A18.B19.C20.D
21. 22. 23. 24. >?
25. 略。
26. (1)解:m∥n 2sinB(2cos2-1)=-cos2B
2sinBcosB=-cos2B tan2B=- ……4分
∵0<2B<π,∴2B=,∴锐角B= ……2分
(2)由tan2B=- B=或
①当B=时,已知b=2,由余弦定理,得:
4=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=2时等号成立) ……3分
∵△ABC的面积S△ABC= acsinB=ac≤
∴△ABC的面积最大值为 ……1分
②当B=时,已知b=2,由余弦定理,得:
4=a2+c2+ac≥2ac+ac=(2+)ac(当且仅当a=c=-时等号成立)
∴ac≤4(2-) ……1分
∵△ABC的面积S△ABC= acsinB=ac≤2-
∴△ABC的面积最大值为2- ……1分
27.解:(Ⅰ)因为,
所以,,.
……………………………………1分
由可知:.
所以,,.
因为,
所以.
所以或. ……………………………………3分
(Ⅱ)假设存在实数,使得数列是等差数列,则.
……………………………………4分
由(Ⅰ)可得:.
所以,即,矛盾.
所以不存在实数,使得数列是等差数列.
…………………………………6分
(Ⅲ)当时,.
所以,且.
所以,即.
所以,且.
所以,数列是以1为首项,2为公比的等比数列
所以. ………………………………8分
因为,且,
所以
.
当时,上式仍然成立.
所以 . ………………………………10分
因为,
所以.
………………………………11分
因为, …………………………………12分
所以
.
28.解:(1)设,则.
,,
由得,
解得:,
所以,直线的方程为
(2)设圆心为,半径为,则
解之得:,
所以,圆的方程为.
(3)设,则,
所以,,
等号当且仅当时取得.
2
2
2
3
A
B
C
D
E
B1
A1
C1
D1
同课章节目录
