六年级下册数学课件 第七单元 《第7课时 统计与可能性》苏教版 (共50张PPT)
文档属性
| 名称 | 六年级下册数学课件 第七单元 《第7课时 统计与可能性》苏教版 (共50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览







文档简介
(共50张PPT)
第七单元
第7课时
统计与可能性
苏教版数学六年级下册
学习目标
1.进一步掌握收集、整理、描述和分析数据的一般方法,能用统计表和统计图表示数据,并能根据实际问题和数据的特点恰当地选择统计图或统计表,对数据进行简单分析;进一步了解平均数的特点和计算方法。
2.体会收集、整理和描述数据的活动过程,感受统计表和不同统计图的特点及作用,体验收集数据的意义,增强数据分析意识。
同学们,今天我们对统计内容进行整理与复习。通过复习,使同学们能系统掌握所学的统计知识,增强数据描述和分析等应用能力。
导入新知
把统计数据填写在一定格式的表格内,用来反映情况、说明问题,这样的表格就叫做(
统计表
)。只含有一个项目的统计表叫(
单式统计表
),含有两个或两个以上统计项目的统计表叫(
复式统计表
)。
复习整理
名称
制作步骤
条形统计图
①根据图纸的大小,画出两条互相垂直的射线。
②在水平射线上,适当分配条形的位置,确定直条的宽度和间隔。
③在与水平射线垂直的射线上,根据数据的大小的具体情况,确定单位长度表示多少。
④根据数据画出长短不同的直条,并注明数量。
折线统计图
制作折线统计图的步骤与制作条形统计图基本相同,只是不画直条,而是按照数据大小描出各点,标数,再用线段依次连接起来。
扇形统计图
①算出各部分数量占总数量的百分数。
②算出表示各部分数量的扇形的圆心角度数。
③取适当的半径画一个圆,并按照前面算出的圆心角的度数,在圆里画出各个扇形。
④在每个扇形中标明所表示的各部分数量名称和所占的百分数,并用不同的颜色或条纹把各个扇形区别开。
复习过程:
(1)汇报课前预习时搜集的已学过的统计知识和知识结构图,互相补充、完善。
板书:
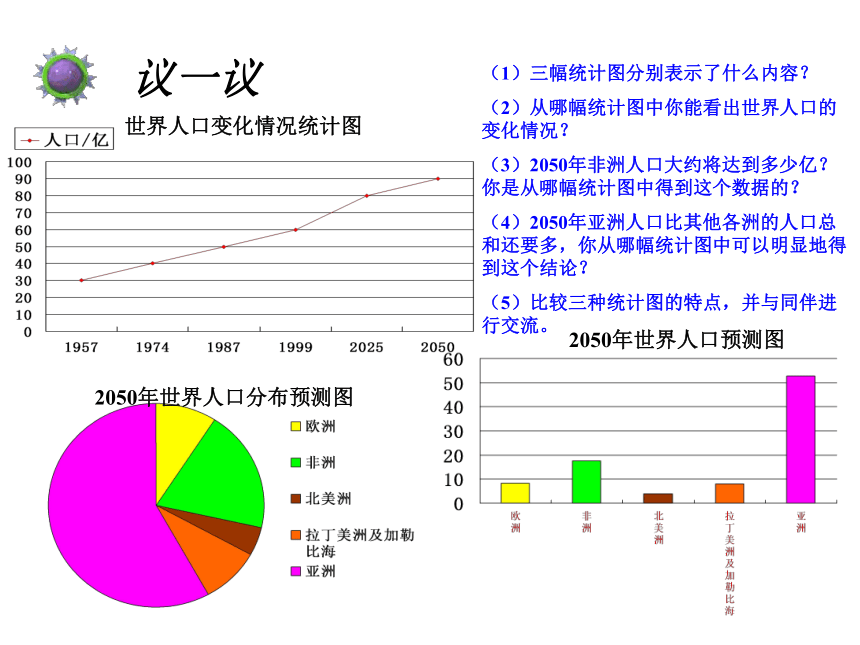
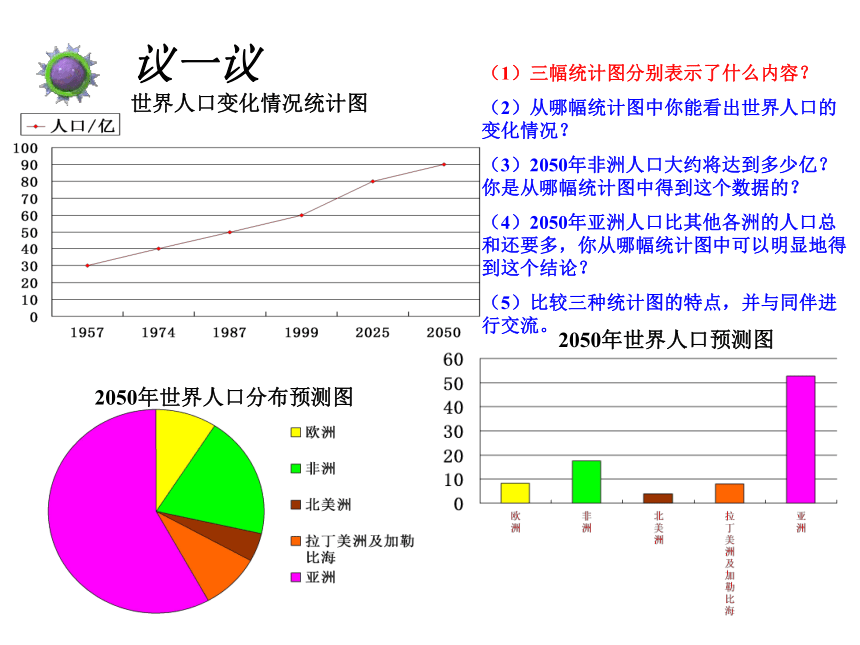
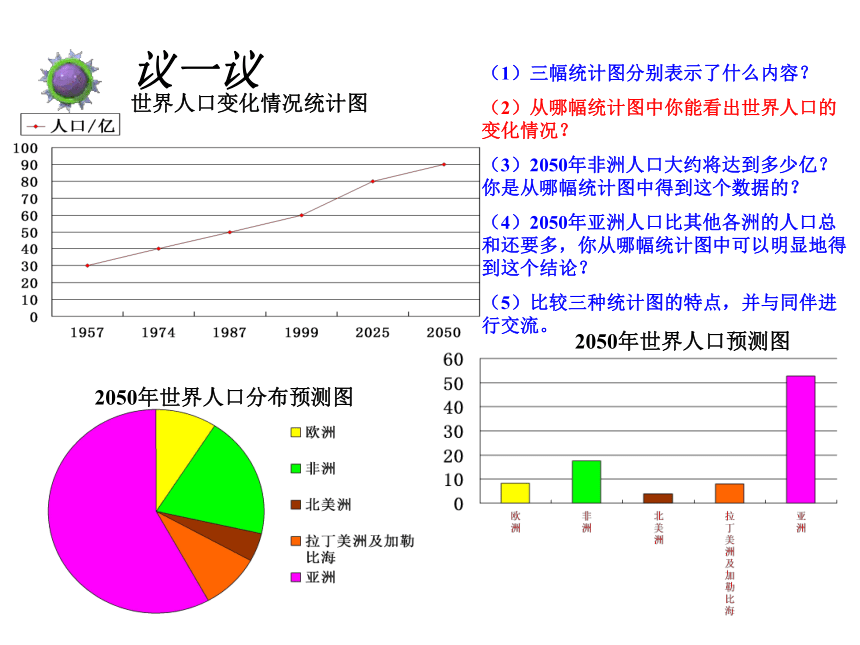
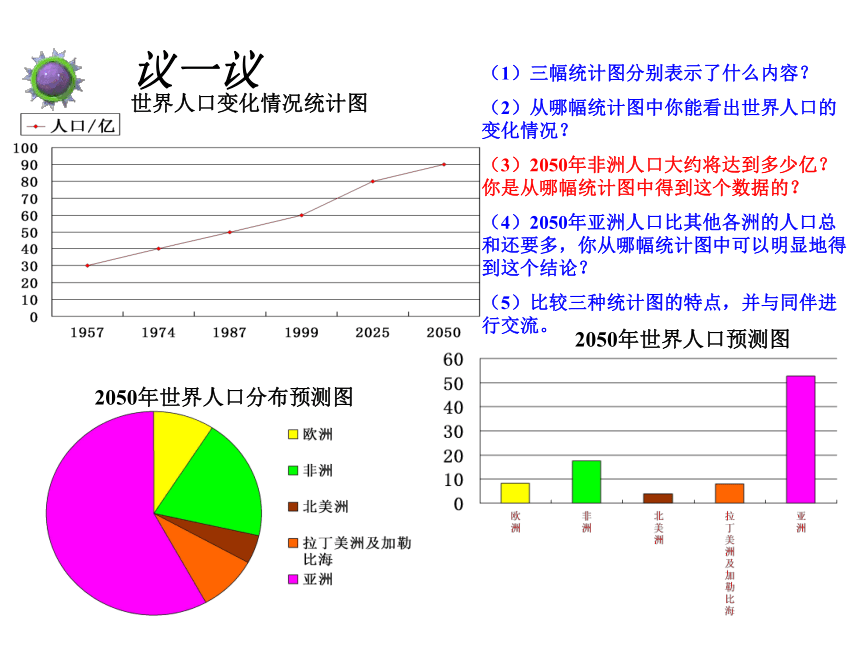
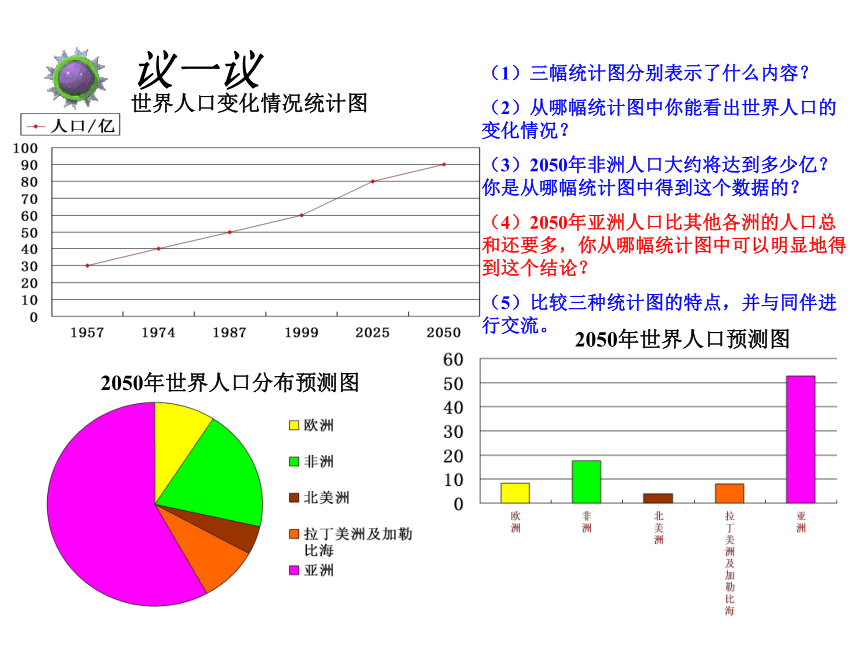
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
分类整理,发现规律
种类
条形统计图
折线统计图
扇形统计图
特点
表示每组中的具体数据
易于比较数据之间的差别
表示部分在总体中的百分比
易于显示数据相对总数的大小
表示数量的多少
易于清楚的看出数量的增减变化情况.
(2)条形统计图、折线统计图和扇形统计图各自的特点和作用
是重点,归纳如下:
条形统计图
折线统计图
扇形统计图
特
点
用一个单位长度表示一定的数量。
用整个圆面积表示总数,用圆内的扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少。
用折线的起伏表示数量的增减变化。
作
用
从图中
能清楚地看出各数量的多少,便于相互比较。
从图中能清楚地看出数量增减变化情况,也能看出数量的多少。
从图中能清楚地看出各部分与总数的百分比,部分与部分之间的关系。
对六(2)班进行调查,对所收集的数据分类用统计表或统计图表示如下:
六(2)班男、女生人数统计表
性别
男生
女生
合计
人数
22
18
40
如果要反映六(2)男、女生人数占全班人数的百分比,应选用什么统计图合适?
(扇形统计图)
六(2)班同学最喜欢的运动项目统计表:
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
用什么统计图来反映六(2)同学最喜欢的运动项目合适呢?
答:(复式条形统计图)
六(2)班同学对自己在各年级的综合表现满意人数的统计表:
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
要反映六(2)班同学对自己在各年级的综合表现满意人数的变化趋势,用什么统计图?
答:折线统计图
六年级一班同学体育达标人数统计图
15
18
27
男生
女生
0
3
6
9
12
21
24
立定跳远
跳绳
投实心球
仰卧起坐
24
22
18
24
15
15
9
7
例2
1.男生达标人数比女生达标人数多的有什么项目?有女生达标人数比男生达标人数多的项目吗?
2.女生仰卧起坐达标人数比跳绳达标人数少百分之几?
(24-7)÷24≈0.708=70.8%
如图
某电台“市民热线”对上周的热线电话进行了分类统计其中有关房产城建的电话有30个。有关环境保护的有多少个?
例3
40%
20%
10%
房
环
解
30÷20%=150
150
10%=15
解:设有关环境保护的有x个,则
30:x=20%:10%
20%x=30
10%
x=15
分析数据:
在统计中,用(
平均数
)作为一组数据的代表比较稳定可靠,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映也是充分,但容易受极端数据的影响。用(
中位数
)或(
众数
)作为一组数据的代表,可靠性比较差,但它们通常不受极端数据的影响,并且算法简便。当一组数据中个别数据变动较大时,适合选择(
中位数
)或(
众数
)来表示这组数据的集中趋势。
平均数
中位数
众
数
反映总体平均水平
反映中等水平
反映多数集中水平
平均数
中位数
众
数
例2
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
①???
在上面两组数据中,
各是多少?
a.???
找出中位数和众数。
b.???
计算平均数。
②???
不用计算,你能发现上面两组数据的平均数,中位数和众数之间的大小关系吗?
学生在小组中交流,说一说各自的思维过程和结果。
③???
你认为用什么数表示上面两组数据的一般水平比较合适?
让同学们说说自己的看法,并说明理由。
平均数、中位数和众数
第一组数据
平均数
(1.40+1.41×3+...+1.58×3)÷(1+3+...+3)≈1.50
中位数
1.52
众数
1.52
第二组数据
平均数
(30×2+33×4+...+48×3)÷(2+4+...+3)
=39.6
中位数是39
众数是39
(2)不用计算,能发现两组数据的平均数、中位数和众数
之间的大小关系吗?
不用计算,能发现两组数据的平均数、中位数和众数之间的大小关系。
在第一组数据中,中位数和众数相等,平均数小于中位数和众数,第二组数据中,中位数和众数相等,平均数大于中位数和众数。
(3)用什么统计量表示上面两组数据的一般水平比较合适?
分析:在这两组数据中,最大数据与最小数据相差不太大,
故用平均数可以反映这两组数据的总体水平。
相同点:
都可以描述一组数据的“平均水平”的特征数。
不同点:
平均数的大小与一组数据里的每个数据都有关系,任何数据的变
化都可能引起平均值的变化。易受极端值影响。
中位数仅与数列的排列位置有关。适用于数据中个别数据变化较
大时。
众数是一组数据中出现次数最多的数据。一组数据中的众数可能
不止一个,也可能没有!
小学阶段学过的可能性知识,学生评价、补充与完善。
能用“一定”、“可能”、“不可能”等词描述事件发生的可能性。
能列出简单事件所有可能发生的结果。
可能性
能按指定的可能性大小设计方案。
能用分数、百分数表示可能性的大小。
能通过实验来估计可能性的大小。
一、独立完成,集体交流
1、下列这些事情发生的可能性请选择用“可能”、“不可能”、“一定”表述。
⑴下周一会下雨。(
)
⑵太阳从西边出来。(
)
⑶水在零度以下会结冰。(
)
⑷远距离投球进篮。
(
)
2、将扑克牌中黑桃A、红桃k、梅花A、方块J各一张放在一起,混合后从中
任意取出一张,说一说:
⑴如只按字母区分,有几种可能的结果?
⑵如只按花色区分,有几种可能的结果?
3、学校举行篮球比赛,裁判员抛硬币来决定谁开球,出现正面的可能性与
出现反面的可能性是(
)的,都是(
)。
1
2
4、一个盒子里有20个白球,9个黄球,1个黑球,任意摸一个球,摸到
(
)球的可能性最大,摸到(
)球的可能性最小。
5、小华有一粒骰子,他掷一次,得到的数字大于4的可能性是(
),
得到的数字等于4的可能性是(
),得到的数字小于4的可能性是
(
)。
6、王叔叔练习投篮一共投了50次,投中了31次,如果他再投10次,你
估计他会投中(
)次。他投篮的命中率是(
)。
1
3
1
6
1
2
8、口袋里有大小相同的10个球,5个红球,2个黄球,3个绿球,从中任意
摸出1个球。
(1)摸出的球的颜色有(
)种可能。
(2)摸到红球的可能性是(
)。
(3)摸到黄球的可能性是(
)。
1
2
1
5
分析:此题是对判定游戏公平这一能力的考查。谁的方法中代表三个人的事件出现的可能性相等,则选谁的方法。
解答:第一种方法不合理。在圆形转盘上按三人的年龄的大小来分,显然表哥所对应的区域要大,指针指向表哥的可能性就大,表哥应得可能性就打,因此不合理。
第二种方法公平。在第2个圆形转盘中,代表三方的区域大小相同,这三个人获胜的可能性各是3分之1,因此公平。
第三种方法公平。设计三个签,在其中一个上面做上记号,同时抽签并打开,那么三个人抽到做记号签的可能性相等,因此也公平。
课后练习
再
见
第七单元
第7课时
统计与可能性
苏教版数学六年级下册
学习目标
1.进一步掌握收集、整理、描述和分析数据的一般方法,能用统计表和统计图表示数据,并能根据实际问题和数据的特点恰当地选择统计图或统计表,对数据进行简单分析;进一步了解平均数的特点和计算方法。
2.体会收集、整理和描述数据的活动过程,感受统计表和不同统计图的特点及作用,体验收集数据的意义,增强数据分析意识。
同学们,今天我们对统计内容进行整理与复习。通过复习,使同学们能系统掌握所学的统计知识,增强数据描述和分析等应用能力。
导入新知
把统计数据填写在一定格式的表格内,用来反映情况、说明问题,这样的表格就叫做(
统计表
)。只含有一个项目的统计表叫(
单式统计表
),含有两个或两个以上统计项目的统计表叫(
复式统计表
)。
复习整理
名称
制作步骤
条形统计图
①根据图纸的大小,画出两条互相垂直的射线。
②在水平射线上,适当分配条形的位置,确定直条的宽度和间隔。
③在与水平射线垂直的射线上,根据数据的大小的具体情况,确定单位长度表示多少。
④根据数据画出长短不同的直条,并注明数量。
折线统计图
制作折线统计图的步骤与制作条形统计图基本相同,只是不画直条,而是按照数据大小描出各点,标数,再用线段依次连接起来。
扇形统计图
①算出各部分数量占总数量的百分数。
②算出表示各部分数量的扇形的圆心角度数。
③取适当的半径画一个圆,并按照前面算出的圆心角的度数,在圆里画出各个扇形。
④在每个扇形中标明所表示的各部分数量名称和所占的百分数,并用不同的颜色或条纹把各个扇形区别开。
复习过程:
(1)汇报课前预习时搜集的已学过的统计知识和知识结构图,互相补充、完善。
板书:
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
世界人口变化情况统计图
2050年世界人口预测图
2050年世界人口分布预测图
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅统计图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流。
议一议
分类整理,发现规律
种类
条形统计图
折线统计图
扇形统计图
特点
表示每组中的具体数据
易于比较数据之间的差别
表示部分在总体中的百分比
易于显示数据相对总数的大小
表示数量的多少
易于清楚的看出数量的增减变化情况.
(2)条形统计图、折线统计图和扇形统计图各自的特点和作用
是重点,归纳如下:
条形统计图
折线统计图
扇形统计图
特
点
用一个单位长度表示一定的数量。
用整个圆面积表示总数,用圆内的扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少。
用折线的起伏表示数量的增减变化。
作
用
从图中
能清楚地看出各数量的多少,便于相互比较。
从图中能清楚地看出数量增减变化情况,也能看出数量的多少。
从图中能清楚地看出各部分与总数的百分比,部分与部分之间的关系。
对六(2)班进行调查,对所收集的数据分类用统计表或统计图表示如下:
六(2)班男、女生人数统计表
性别
男生
女生
合计
人数
22
18
40
如果要反映六(2)男、女生人数占全班人数的百分比,应选用什么统计图合适?
(扇形统计图)
六(2)班同学最喜欢的运动项目统计表:
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
用什么统计图来反映六(2)同学最喜欢的运动项目合适呢?
答:(复式条形统计图)
六(2)班同学对自己在各年级的综合表现满意人数的统计表:
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
要反映六(2)班同学对自己在各年级的综合表现满意人数的变化趋势,用什么统计图?
答:折线统计图
六年级一班同学体育达标人数统计图
15
18
27
男生
女生
0
3
6
9
12
21
24
立定跳远
跳绳
投实心球
仰卧起坐
24
22
18
24
15
15
9
7
例2
1.男生达标人数比女生达标人数多的有什么项目?有女生达标人数比男生达标人数多的项目吗?
2.女生仰卧起坐达标人数比跳绳达标人数少百分之几?
(24-7)÷24≈0.708=70.8%
如图
某电台“市民热线”对上周的热线电话进行了分类统计其中有关房产城建的电话有30个。有关环境保护的有多少个?
例3
40%
20%
10%
房
环
解
30÷20%=150
150
10%=15
解:设有关环境保护的有x个,则
30:x=20%:10%
20%x=30
10%
x=15
分析数据:
在统计中,用(
平均数
)作为一组数据的代表比较稳定可靠,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映也是充分,但容易受极端数据的影响。用(
中位数
)或(
众数
)作为一组数据的代表,可靠性比较差,但它们通常不受极端数据的影响,并且算法简便。当一组数据中个别数据变动较大时,适合选择(
中位数
)或(
众数
)来表示这组数据的集中趋势。
平均数
中位数
众
数
反映总体平均水平
反映中等水平
反映多数集中水平
平均数
中位数
众
数
例2
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
①???
在上面两组数据中,
各是多少?
a.???
找出中位数和众数。
b.???
计算平均数。
②???
不用计算,你能发现上面两组数据的平均数,中位数和众数之间的大小关系吗?
学生在小组中交流,说一说各自的思维过程和结果。
③???
你认为用什么数表示上面两组数据的一般水平比较合适?
让同学们说说自己的看法,并说明理由。
平均数、中位数和众数
第一组数据
平均数
(1.40+1.41×3+...+1.58×3)÷(1+3+...+3)≈1.50
中位数
1.52
众数
1.52
第二组数据
平均数
(30×2+33×4+...+48×3)÷(2+4+...+3)
=39.6
中位数是39
众数是39
(2)不用计算,能发现两组数据的平均数、中位数和众数
之间的大小关系吗?
不用计算,能发现两组数据的平均数、中位数和众数之间的大小关系。
在第一组数据中,中位数和众数相等,平均数小于中位数和众数,第二组数据中,中位数和众数相等,平均数大于中位数和众数。
(3)用什么统计量表示上面两组数据的一般水平比较合适?
分析:在这两组数据中,最大数据与最小数据相差不太大,
故用平均数可以反映这两组数据的总体水平。
相同点:
都可以描述一组数据的“平均水平”的特征数。
不同点:
平均数的大小与一组数据里的每个数据都有关系,任何数据的变
化都可能引起平均值的变化。易受极端值影响。
中位数仅与数列的排列位置有关。适用于数据中个别数据变化较
大时。
众数是一组数据中出现次数最多的数据。一组数据中的众数可能
不止一个,也可能没有!
小学阶段学过的可能性知识,学生评价、补充与完善。
能用“一定”、“可能”、“不可能”等词描述事件发生的可能性。
能列出简单事件所有可能发生的结果。
可能性
能按指定的可能性大小设计方案。
能用分数、百分数表示可能性的大小。
能通过实验来估计可能性的大小。
一、独立完成,集体交流
1、下列这些事情发生的可能性请选择用“可能”、“不可能”、“一定”表述。
⑴下周一会下雨。(
)
⑵太阳从西边出来。(
)
⑶水在零度以下会结冰。(
)
⑷远距离投球进篮。
(
)
2、将扑克牌中黑桃A、红桃k、梅花A、方块J各一张放在一起,混合后从中
任意取出一张,说一说:
⑴如只按字母区分,有几种可能的结果?
⑵如只按花色区分,有几种可能的结果?
3、学校举行篮球比赛,裁判员抛硬币来决定谁开球,出现正面的可能性与
出现反面的可能性是(
)的,都是(
)。
1
2
4、一个盒子里有20个白球,9个黄球,1个黑球,任意摸一个球,摸到
(
)球的可能性最大,摸到(
)球的可能性最小。
5、小华有一粒骰子,他掷一次,得到的数字大于4的可能性是(
),
得到的数字等于4的可能性是(
),得到的数字小于4的可能性是
(
)。
6、王叔叔练习投篮一共投了50次,投中了31次,如果他再投10次,你
估计他会投中(
)次。他投篮的命中率是(
)。
1
3
1
6
1
2
8、口袋里有大小相同的10个球,5个红球,2个黄球,3个绿球,从中任意
摸出1个球。
(1)摸出的球的颜色有(
)种可能。
(2)摸到红球的可能性是(
)。
(3)摸到黄球的可能性是(
)。
1
2
1
5
分析:此题是对判定游戏公平这一能力的考查。谁的方法中代表三个人的事件出现的可能性相等,则选谁的方法。
解答:第一种方法不合理。在圆形转盘上按三人的年龄的大小来分,显然表哥所对应的区域要大,指针指向表哥的可能性就大,表哥应得可能性就打,因此不合理。
第二种方法公平。在第2个圆形转盘中,代表三方的区域大小相同,这三个人获胜的可能性各是3分之1,因此公平。
第三种方法公平。设计三个签,在其中一个上面做上记号,同时抽签并打开,那么三个人抽到做记号签的可能性相等,因此也公平。
课后练习
再
见
