中考数学复习专题——旋转和中心对称的命题角度学案(附答案)
文档属性
| 名称 | 中考数学复习专题——旋转和中心对称的命题角度学案(附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 729.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 21:33:05 | ||
图片预览



文档简介
11544300111760001264920011531600讲次01 旋转
旋转的概念:在平面内,把一个平面图形绕着平面内一个定点沿某一方向转动一个角度,就叫做图形的旋转.这个定点叫做旋转中心.转动的角叫做旋转角
如图所示,false是false绕定点false逆时针旋转false得到的,其中点false与点false叫作对应点,线段false与线段false叫作对应线段,false与false叫作对应角,点false叫作旋转中心,false(或false)的度数叫作旋转的角度.
【注意】旋转中心可以是图形内,也可以是图形外。
【图形旋转的三要素】旋转中心、旋转方向和旋转角.
旋转的特征:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
旋转作图的步骤方法:
1.先确定旋转中心、旋转方向、旋转角;
2.找出图形上的关键点;
3.连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,得到关键点的对应点;
4.按原图的顺序连接这些对应点,即得旋转后的图形.
平移、旋转、轴对称之间的联系:
变化后不改变图形的大小和形状,对应线段相等、对应角相等。
平移、旋转、轴对称之间的区别:
变化方式不同:
平移:将一个图形沿某个方向移动一定距离。
旋转:将一个图形绕一个顶点沿某个方向转一定角度。
轴对称:将一个图形沿一条直线对折。
2)对应线段、对应角之间的关系不同
平移: 变化前后对应线段平行(或在一条直线上),对应点连线平行(或在一条直线上),对应角的两边平行(或在一条直线上)、方向一致。
旋转: 变化前后任意一对对应点与旋转中心的连线所成的角都等于旋转角。
轴对称:对应线段或延长线如果相交,那么交点在对称轴上。
3)确定条件不同
平移:距离与方向;旋转:旋转的三要素;轴对称:对称轴
命题角度一 判断由一个图形旋转而形成的图案
例题1.将false绕点false旋转false得到false,则下列作图正确的是( )
A. B. C. D.
【解析】观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.
【小结】本题考察了旋转的定义.
变式1.下列选项中,能通过旋转把图a变换为图b的是( )
A. B. C. D.
【解析】A、可将图a绕直角顶点顺时针旋转90°可得,正确;
B、可通过轴对称得到,错误;
C、图形形状、大小均不同,任何变换都得不到,错误;
D、旋转变换得不到,错误;
选A.
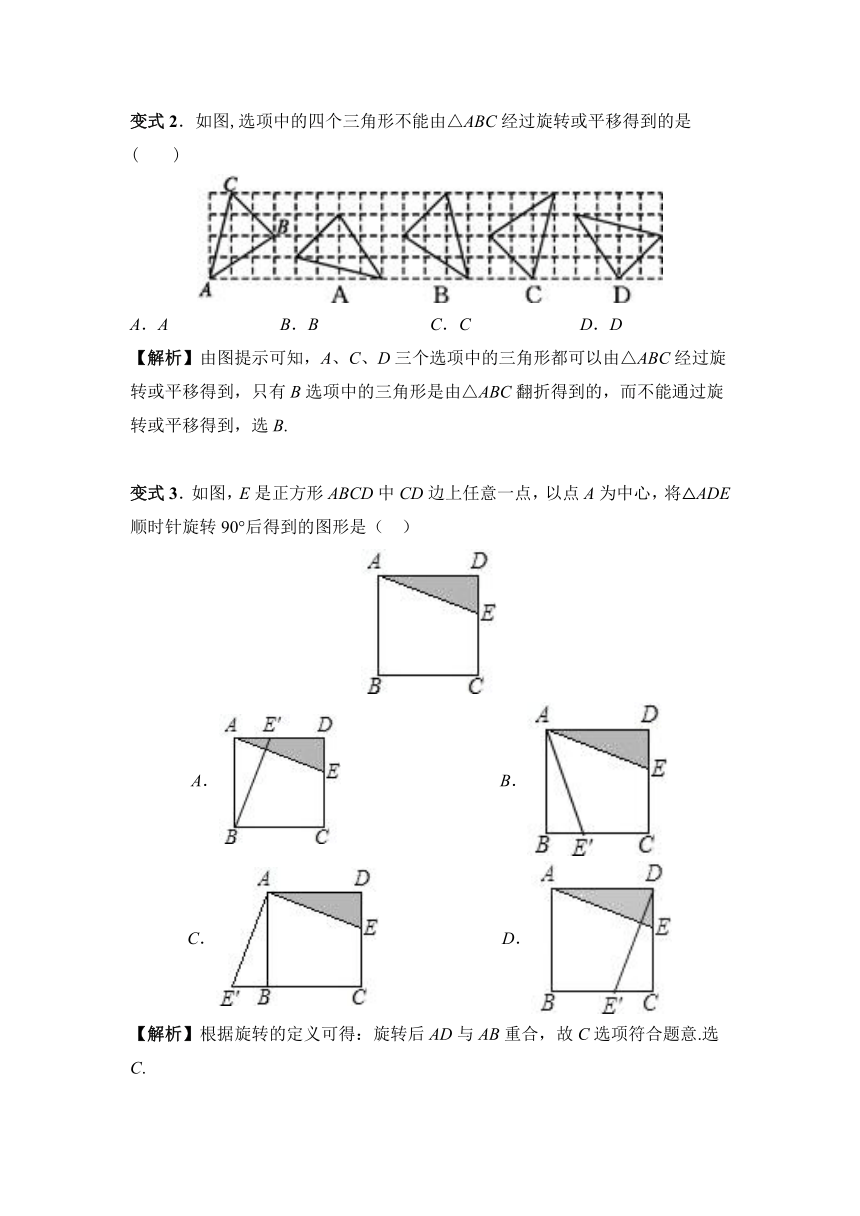
变式2.如图,选项中的四个三角形不能由△ABC经过旋转或平移得到的是( )
A.A B.B C.C D.D
【解析】由图提示可知,A、C、D三个选项中的三角形都可以由△ABC经过旋转或平移得到,只有B选项中的三角形是由△ABC翻折得到的,而不能通过旋转或平移得到,选B.
变式3.如图,E是正方形ABCD中CD边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到的图形是(?? )
A. B.
C. D.
【解析】根据旋转的定义可得:旋转后AD与AB重合,故C选项符合题意.选C.
【小结】本题考查生活中的旋转现象,解题的关键是掌握旋转的性质.
命题角度二 找旋转中心、旋转角度
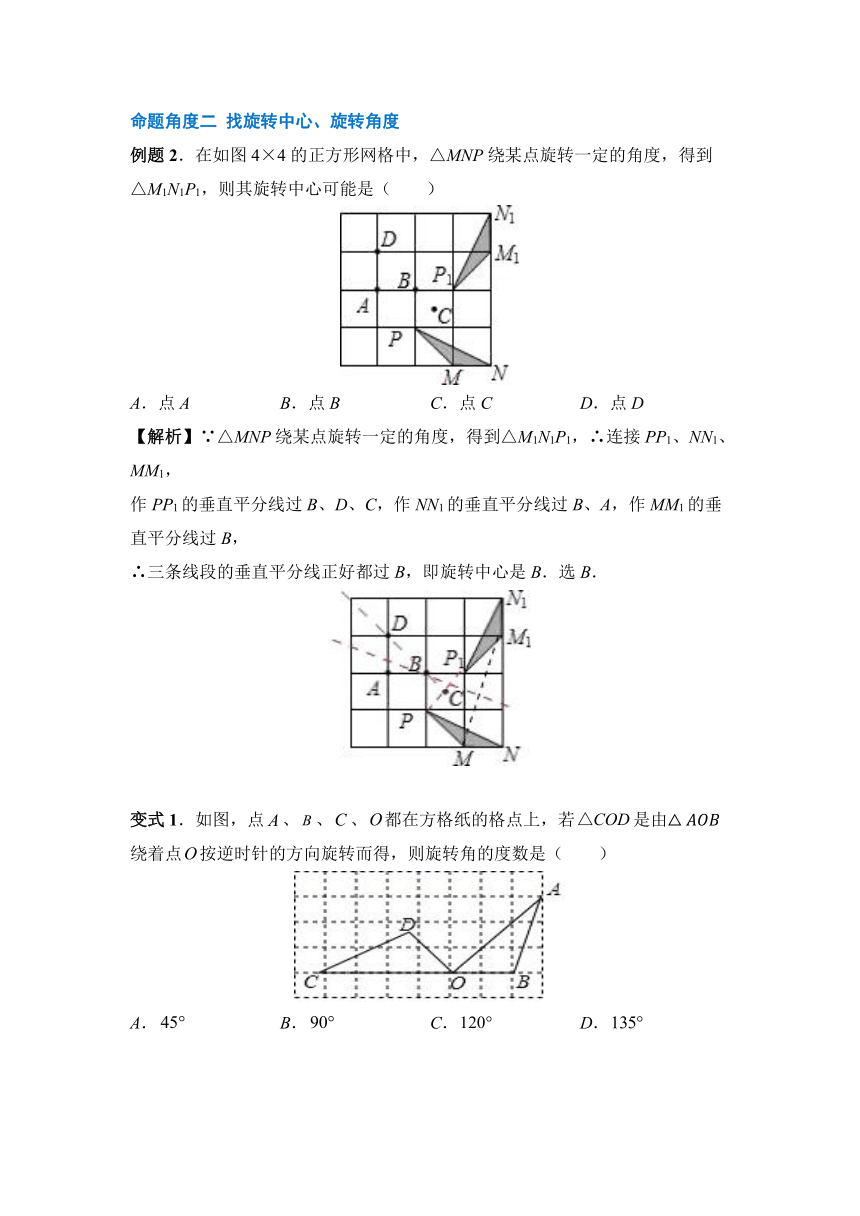
例题2.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
【解析】∵△MNP绕某点旋转一定的角度,得到△M1N1P1,∴连接PP1、NN1、MM1,
作PP1的垂直平分线过B、D、C,作NN1的垂直平分线过B、A,作MM1的垂直平分线过B,
∴三条线段的垂直平分线正好都过B,即旋转中心是B.选B.
变式1.如图,点false、false、false、false都在方格纸的格点上,若false是由△AOB绕着点false按逆时针的方向旋转而得,则旋转角的度数是( )
A.false B.false C.false D.false
【解析】∵△COD是由△AOB绕点O按逆时针方向旋转而得,∴∠AOC为旋转角,
∵∠AOB=45°,∴∠AOC=135°,即旋转角为135°.选D.
变式2.如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( )
A.(1,0) B.(0,0) C.(-1,2) D.(-1,1)
【解析】如图所示,根据旋转的性质,对应点到旋转中心的距离相等,只有(-1,2)点到三角形的三顶点距离相等,故(-1,2)是图形的旋转中心,选C.
变式3.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A.42° B.48° C.52° D.58°
【解析】∵在Rt△ABC中,∠BAC=90°,
将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,
∴∠A′=∠BAC=90°,∠ACA′=48°,
∴∠B′=90°﹣∠ACA′=42°.选A.
命题角度三 旋转的性质
例题3如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
【解析】∵△ADE是由△ABC绕点A旋转100°得到的,
∴∠BAD=100°,AD=AB,
∵点D在BC的延长线上,
∴∠B=∠ADB=false.
选B.
变式1.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( ).
A.15° B.20° C.25° D.30°
【解析】∵正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,
∴∠AOF=90°+40°=130°,OA=OF,
∴∠OFA=(180°-130°)÷2=25°.
选C.
变式2.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
【解析】由题意可得∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180°?α,
选C.
变式3.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB'C'的位置.若∠CAB'=25°则∠ACC''的度数为( )
A.25° B.40° C.65° D.70°
【解析】∵△AB′C′是由△ABC绕点A旋转得到的,
∴∠CAC′=∠BAB′,AC=AC′,
∵∠BAB′=∠BAC-∠CAB′=65°-25°=40°,
∴∠CAC′=40°,
∴∠ACC′=∠AC′C=false(180°-40°)=70°.
选D.
变式4.如图,将△ABC绕点C顺时针旋转m°得到△EDC,若点A、D、E在同一直线上,∠ACB=n°,则∠ADC的度数是( )
A.(m﹣n)° B.(90+n-falsem)° C.(90-falsen+m)° D.(180﹣2n﹣m)°
【分析】
根据旋转的性质即可得到∠ACD和∠CAD的度数,再根据三角形内角和定理进行解答即可.
【解析】
∵将△ABC绕点C顺时针旋转m°得到△EDC.
∴∠DCE=∠ACB=n°,∠ACE=m°,AC=CE,
∴∠ACD=m°-n°,
∵点A,D,E在同一条直线上,
∴∠CAD=false(180°-m°),
∵在△ADC中,∠ADC+∠DAC+∠DCA=180°,
∴∠ADC=180°-∠CAD-∠ACD=180°-false(180°-m°)-(m°-n°)=90°+n°-falsem°=(90+n-falsem)°,
选B.
【小结】
此题考查旋转的性质,关键是根据旋转的性质和三角形内角和解答.解题时注意:对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等.
命题角度四 画旋转图形
例题4.按图中第一、二两行图形的平移、轴对称及旋转等变换规律,填入第三行“?”处的图形应是( )
A. B. C. D.
【解析】根据第一、二行的规律,可知首先将第一个图轴对称得到第二个图,然后将第二个图顺时针旋转90度得到第三个图,通过观察可得B选项的图符合,
选B.
变式1.在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转false,向右平移 B.逆时针旋转false,向右平移
C.顺时针旋转false,向下平移 D.逆时针旋转false,向下平移
【解析】由已知可得,顺时针旋转90°,向右平移,能把右下角完全填补.只有选项A符合条件,其他选项不能符合条件.
选A.
变式2.在图中,将方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
【解析】根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是
.
选B.
变式3.如图,将方格纸中的图形绕点false逆时针旋转false后得到的图形是( )
A. B. C. D.
【解析】如图所示:将方格纸中的图形绕点O逆时针旋转90°后得到的图形是
.
选C.
命题角度五 利用旋转设计图案
例题5下面四个图案中,不能由基本图案旋转得到的是( )
A. B. C. D.
【解析】
A.可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B.可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C.可由一个基本图形绕其中心旋转180°得到;
D.不能由基本图案旋转得到.
选D.
变式1.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A.B.C. D.
【解析】先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
选B.
变式2.如图,是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是 ( )
A. B. C. D.
【解析】由图可得下一个呈现出来的图形是第二个,选B.
变式3.如图所示的图案是由下列哪个图形旋转得到的( )
A. B.
C. D.
【解析】由图可得,如图所示的图案是由绕着一端旋转3次,每次旋转90°得到的,
选D.
命题角度六 求旋转对称图形的旋转角度
例题6.如图,香港特别行政区标志紫荆花图案绕中心旋转false°后能与原来的图案互相重合,则false的最小值为( )
A.45 B.60 C.72 D.144
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是false,并且圆具有旋转不变性,因而旋转false的整数倍,就可以与自身重合.
【解析】该图形被平分成五部分,旋转false的整数倍,就可以与自身重合,故false的最小值为false.选false.
【小结】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
变式1.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是( )
A.甲 B.乙 C.丙 D.丁
【解析】圆被平分成八部分,旋转45°的整数倍,就可以与自身重合,因而甲,丙,丁都正确;错误的是乙.选B.
变式2.如图是几种常见的汽车轮毂图案,图案围绕中心旋转90°后能与原来的图案重合的是( )
A. B. C. D.
【分析】
根据各选项图形以及旋转的概念即可逐一判断.
【解析】
A、此图形旋转60°或60°的整数倍能与原来的图案重合;
B、此图形旋转45°或45°的整数倍能与原来的图案重合;
C、此图形旋转72°或72°的整数倍能与原来的图案重合;
D、此图形旋转36°或36°的整数倍能与原来的图案重合;
故答案为:B.
【小结】
本题考查了旋转的概念,解题的关键是熟知旋转的概念.
10553700104267001264920011531600讲次0 2中心对称
中心对称概念:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫作对称中心.这两个图形旋转后能重合的对应点叫作关于对称中心的对称点.
如图,false绕着点false旋转false后,与false完全重合,则称false和false关于点false对称,点false是点false关于点false的对称点.
中心对称图形概念:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫作中心对称图形,这个点就是它的对称中心.
中心对称与中心对称图形的区别与联系:
中心对称
中心对称图形
区别
(1)是针对两个图形而言的.
(2)是指两个图形的(位置)关系.
(3)对称点在两个图形上.
(4)对称中心在两个图形之间.
(1)是针对一个图形而言的.
(2)是指具有某种性质的一个图形.
(3)对称点在一个图形上.
(4)对称中心在图形上.
联系
(1)都是通过把图形旋转180°重合来定义的.
(2)两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称
中心对称的性质:
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
2.中心对称的两个图形是全等图形.
找对称中心的方法和步骤:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
关于原点对称的点的坐标规律
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点
P’(-x,-y)
命题角度一 中心对称图形的识别
例题1.下列图形中,既是轴对称图形又是中心对称图形的是false false
A. B. C. D.
【解析】
A. 是轴对称图形,但不是中心对称图形,故不符合题意;
B. 不是轴对称图形,是中心对称图形,故不符合题意;
C. 是轴对称图形,但不是中心对称图形,故不符合题意;
D. 既是轴对称图形又是中心对称图形,故符合题意.
选D.
变式1.下列图形中,是中心对称图形的是( )
A. B. C. D.
【解析】
A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项正确;
选D.
变式2.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解析】A.是轴对称图形,不是中心对称图形;
B.是轴对称图形,也是中心对称图形;
C.是轴对称图形,不是中心对称图形;
D.是轴对称图形,不是中心对称图形.
选B.
变式3.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
【解析】A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,不是中心对称图形,故不符合题意;
C、是轴对称图形,也是中心对称图形,故符合题意;
D、是轴对称图形,不是中心对称图形,故不符合题意,
选C.
命题角度二 判断中心对称图形的对称中心
例题2.如图,已知图形是中心对称图形,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
【解析】∵此图形是中心对称图形,∴对称中心是线段FC的中点。
选D.
变式1.如图所示的中心对称图形中,对称中心是( )
A.false B.false C.false D.false
【解析】
如图所示的中心对称图形中,对称中心是O2.
选B.
变式2.如图,将false绕点false旋转false得到false设点false的坐标为false, 则点false的坐标为( )
A.false B.false
C.false D.false
【分析】
根据旋转变换的对应点关于旋转中心对称,再根据中点公式列式求解即可.
【解析】
根据题意,点A、A′关于点C对称,
设点A’的坐标是(x,y),
则false,false,解得x=?a+2,y=?b+2,
∴点A’的坐标是false.
选C.
【小结】
本题考查了利用旋转进行坐标与图形的变化,根据旋转的性质得出点A、A′关于点C成中心对称是解题的关键,还需注意中点公式的利用,也是容易出错的地方.
命题角度三 中心对称的性质
例题3.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点false是对称点 B.false C.false D.false
【解析】
A、正确;
B、正确;
C、根据OA=OA′,OB=OB′,∠AOB=∠A′OB′,得到△AOB≌△A′OB′.则∠ABO=∠A′B′O,则AB∥A′B′,正确;
D、两个角不是对应角,错误.
选D.
变式1.如图是一个以O为对称中心的中心对称图形,若∠A=30°, ∠C=90°,OC=1,则AB的长为( )
A.2 B.4 C.false D.false
【解析】由中心对称图形的性质,可得:AO=BO,
∴AB=2OA,
在Rt△AOC中,
∠A=30°, ∠C=90°,OC=1,
∴OA=2OC=2,∴ AB=4.
选B.
变式2.如图所示,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是( )
A.AB=A′B′,BC=B′C′ B.AB∥A′B′,BC∥B′C′
C.S△ABC=S△A′B′C′ D.△ABC≌△A′OC′
【分析】根据成中心对称图形的性质:对应边平行且相等,对应角相等,图形全等,面积相等进行判断.
【解析】∵△ABC与△A′BC′是成中心对称的两个图形,
∴AB=A′B′,BC=B′C′,AB∥A′B′,BC∥B′C′,S△ABC=S△A′B′C′,
无法得到:△ABC≌△A′OC′.所以选D.
变式3.如图,false与false关于false成中心对称,下列结论中不一定成立的是( )
A.false B.false
C.false D.false
【分析】根据中心对称性质逐个提示即可.
【解析】A. false,本选项不一定正确;
B. false,对应边相等;
C. false,对应边相等;
D. false,对应边相等;
选A
【小结】考核知识点:中心对称性质.理解中心对称的基本性质是关键.
命题角度四 根据中心对称的性质求面积
例题4.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
【解析】由图形可知,长方形的面积=10×4=40cm2,再根据中心对称的性质得,图中阴影部分的面积即是长方形面积的一半,则图中阴影部分的面积=false×40=20cm2,选A.
变式1.用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都正确 D.甲、乙都不正确
【解析】如图:图形2中,直线m经过了大长方形和小长方形的对角线的交点,所以两旁的图形的面积都是大长方形和小长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即甲做法正确;
图形3中,经过大正方形和图形外不添补的长方形的对角线的交点,直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即乙做法正确.
选C.
变式2.如图,在面积为12的□ABCD中,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交AB、CD于点E、F,若AE=2EB,则图中阴影部分的面积等于( )
A.3 B.1 C.false D.false
【解析】
∵□ABCD,
∴AO=OC,∠CAB=∠DCO.
∵在△AOE和△COF中AO=OC,∠CAB=∠DCO,∠AOE=∠COF.
∴△AOE≌△COF.
∴S△FCO=S△OAE.
∵面积为12的□ABCD,
∴S△DAB=6.
过点D做DG⊥AB,OH⊥AB,
∵O为中点,
∴OH=falseDG.
∴S阴影=SOAB=false S△DAB=3.
选A.
【小结】本题考查的是平行四边形,熟练掌握平行四边形的性质是解题的关键.
命题角度五 在方格纸中补画图形使之成为中心对称图形
例题5.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
【解析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,通过观察发现,当涂黑②时,所形成的图形关于点A中心对称。选B。
变式1.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
【解析】
利用轴对称图形的性质以及中心对称图形的性质提示得出符合题意的图形即可.如图所示:组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
选C.
变式2.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中涂色部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
【分析】根据中心对称图形的概念,如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形.将④涂黑后,与图中阴影部分构成的图形绕第三个正方形的中心旋转180°后,这个图形能与自身重合,是中心对称图.
【解析】将④涂黑后,与图中阴影部分构成的图形绕第三个正方形的中心旋转180°后,这个图形能与自身重合,是中心对称图.
选D.
【小结】本题考查的是利用旋转设计图案,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
命题角度六 关于原点对称的点的坐标
例题6.在平面直角坐标系中,点false关于原点对称的点的坐标是( )
A.false B.false C.false D.false
【解析】点P(-3,-5)关于原点对称的点的坐标是(3,5),
选C.
变式1.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为()
A.33 B.-33 C.-7 D.7
【解析】关于原点对称的两个点,横坐标和纵坐标分别互为相反数.根据性质可得:a=-13,b=20,则a+b=-13+20=7.
变式2.在平面直角坐标系中,点false关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解析】∵false,∴点false在第二象限,
∴点false关于原点对称点在第四象限.
选D.
变式3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则yx的值是( )
A.2 B.false C.4 D.8
【解析】∵点A(x,y-4)与点B(1-y,2x)关于原点对称,
∴false 解得:false 则yx=2-1=false.
选B.
变式4.若在平面直角坐标系内A(m-1,6),B(-2,n)两点关于原点对称,则m+n的值为( )
A.9 B.-3 C.3 D.5
【解析】∵在平面直角坐标系内A(m-1,6),B(-2,n)两点关于原点对称,
∴m-1+(-2)=0,6+n=0,
∴m=3,n=-6,
∴m+n=3+(-6)=-3.
选B.
旋转的概念:在平面内,把一个平面图形绕着平面内一个定点沿某一方向转动一个角度,就叫做图形的旋转.这个定点叫做旋转中心.转动的角叫做旋转角
如图所示,false是false绕定点false逆时针旋转false得到的,其中点false与点false叫作对应点,线段false与线段false叫作对应线段,false与false叫作对应角,点false叫作旋转中心,false(或false)的度数叫作旋转的角度.
【注意】旋转中心可以是图形内,也可以是图形外。
【图形旋转的三要素】旋转中心、旋转方向和旋转角.
旋转的特征:
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
旋转作图的步骤方法:
1.先确定旋转中心、旋转方向、旋转角;
2.找出图形上的关键点;
3.连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,得到关键点的对应点;
4.按原图的顺序连接这些对应点,即得旋转后的图形.
平移、旋转、轴对称之间的联系:
变化后不改变图形的大小和形状,对应线段相等、对应角相等。
平移、旋转、轴对称之间的区别:
变化方式不同:
平移:将一个图形沿某个方向移动一定距离。
旋转:将一个图形绕一个顶点沿某个方向转一定角度。
轴对称:将一个图形沿一条直线对折。
2)对应线段、对应角之间的关系不同
平移: 变化前后对应线段平行(或在一条直线上),对应点连线平行(或在一条直线上),对应角的两边平行(或在一条直线上)、方向一致。
旋转: 变化前后任意一对对应点与旋转中心的连线所成的角都等于旋转角。
轴对称:对应线段或延长线如果相交,那么交点在对称轴上。
3)确定条件不同
平移:距离与方向;旋转:旋转的三要素;轴对称:对称轴
命题角度一 判断由一个图形旋转而形成的图案
例题1.将false绕点false旋转false得到false,则下列作图正确的是( )
A. B. C. D.
【解析】观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.
【小结】本题考察了旋转的定义.
变式1.下列选项中,能通过旋转把图a变换为图b的是( )
A. B. C. D.
【解析】A、可将图a绕直角顶点顺时针旋转90°可得,正确;
B、可通过轴对称得到,错误;
C、图形形状、大小均不同,任何变换都得不到,错误;
D、旋转变换得不到,错误;
选A.
变式2.如图,选项中的四个三角形不能由△ABC经过旋转或平移得到的是( )
A.A B.B C.C D.D
【解析】由图提示可知,A、C、D三个选项中的三角形都可以由△ABC经过旋转或平移得到,只有B选项中的三角形是由△ABC翻折得到的,而不能通过旋转或平移得到,选B.
变式3.如图,E是正方形ABCD中CD边上任意一点,以点A为中心,将△ADE顺时针旋转90°后得到的图形是(?? )
A. B.
C. D.
【解析】根据旋转的定义可得:旋转后AD与AB重合,故C选项符合题意.选C.
【小结】本题考查生活中的旋转现象,解题的关键是掌握旋转的性质.
命题角度二 找旋转中心、旋转角度
例题2.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
【解析】∵△MNP绕某点旋转一定的角度,得到△M1N1P1,∴连接PP1、NN1、MM1,
作PP1的垂直平分线过B、D、C,作NN1的垂直平分线过B、A,作MM1的垂直平分线过B,
∴三条线段的垂直平分线正好都过B,即旋转中心是B.选B.
变式1.如图,点false、false、false、false都在方格纸的格点上,若false是由△AOB绕着点false按逆时针的方向旋转而得,则旋转角的度数是( )
A.false B.false C.false D.false
【解析】∵△COD是由△AOB绕点O按逆时针方向旋转而得,∴∠AOC为旋转角,
∵∠AOB=45°,∴∠AOC=135°,即旋转角为135°.选D.
变式2.如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( )
A.(1,0) B.(0,0) C.(-1,2) D.(-1,1)
【解析】如图所示,根据旋转的性质,对应点到旋转中心的距离相等,只有(-1,2)点到三角形的三顶点距离相等,故(-1,2)是图形的旋转中心,选C.
变式3.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A.42° B.48° C.52° D.58°
【解析】∵在Rt△ABC中,∠BAC=90°,
将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,
∴∠A′=∠BAC=90°,∠ACA′=48°,
∴∠B′=90°﹣∠ACA′=42°.选A.
命题角度三 旋转的性质
例题3如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
【解析】∵△ADE是由△ABC绕点A旋转100°得到的,
∴∠BAD=100°,AD=AB,
∵点D在BC的延长线上,
∴∠B=∠ADB=false.
选B.
变式1.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( ).
A.15° B.20° C.25° D.30°
【解析】∵正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,
∴∠AOF=90°+40°=130°,OA=OF,
∴∠OFA=(180°-130°)÷2=25°.
选C.
变式2.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
【解析】由题意可得∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180°?α,
选C.
变式3.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB'C'的位置.若∠CAB'=25°则∠ACC''的度数为( )
A.25° B.40° C.65° D.70°
【解析】∵△AB′C′是由△ABC绕点A旋转得到的,
∴∠CAC′=∠BAB′,AC=AC′,
∵∠BAB′=∠BAC-∠CAB′=65°-25°=40°,
∴∠CAC′=40°,
∴∠ACC′=∠AC′C=false(180°-40°)=70°.
选D.
变式4.如图,将△ABC绕点C顺时针旋转m°得到△EDC,若点A、D、E在同一直线上,∠ACB=n°,则∠ADC的度数是( )
A.(m﹣n)° B.(90+n-falsem)° C.(90-falsen+m)° D.(180﹣2n﹣m)°
【分析】
根据旋转的性质即可得到∠ACD和∠CAD的度数,再根据三角形内角和定理进行解答即可.
【解析】
∵将△ABC绕点C顺时针旋转m°得到△EDC.
∴∠DCE=∠ACB=n°,∠ACE=m°,AC=CE,
∴∠ACD=m°-n°,
∵点A,D,E在同一条直线上,
∴∠CAD=false(180°-m°),
∵在△ADC中,∠ADC+∠DAC+∠DCA=180°,
∴∠ADC=180°-∠CAD-∠ACD=180°-false(180°-m°)-(m°-n°)=90°+n°-falsem°=(90+n-falsem)°,
选B.
【小结】
此题考查旋转的性质,关键是根据旋转的性质和三角形内角和解答.解题时注意:对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等.
命题角度四 画旋转图形
例题4.按图中第一、二两行图形的平移、轴对称及旋转等变换规律,填入第三行“?”处的图形应是( )
A. B. C. D.
【解析】根据第一、二行的规律,可知首先将第一个图轴对称得到第二个图,然后将第二个图顺时针旋转90度得到第三个图,通过观察可得B选项的图符合,
选B.
变式1.在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转false,向右平移 B.逆时针旋转false,向右平移
C.顺时针旋转false,向下平移 D.逆时针旋转false,向下平移
【解析】由已知可得,顺时针旋转90°,向右平移,能把右下角完全填补.只有选项A符合条件,其他选项不能符合条件.
选A.
变式2.在图中,将方格纸中的图形绕O点顺时针旋转90°得到的图形是( )
A. B. C. D.
【解析】根据旋转的性质可知,绕O点顺时针旋转90°得到的图形是
.
选B.
变式3.如图,将方格纸中的图形绕点false逆时针旋转false后得到的图形是( )
A. B. C. D.
【解析】如图所示:将方格纸中的图形绕点O逆时针旋转90°后得到的图形是
.
选C.
命题角度五 利用旋转设计图案
例题5下面四个图案中,不能由基本图案旋转得到的是( )
A. B. C. D.
【解析】
A.可由一个基本“花瓣”绕其中心经过7次旋转,每次旋转45°得到;
B.可由一个基本“菱形”绕其中心经过5次旋转,每次旋转60°得到;
C.可由一个基本图形绕其中心旋转180°得到;
D.不能由基本图案旋转得到.
选D.
变式1.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A.B.C. D.
【解析】先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
选B.
变式2.如图,是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是 ( )
A. B. C. D.
【解析】由图可得下一个呈现出来的图形是第二个,选B.
变式3.如图所示的图案是由下列哪个图形旋转得到的( )
A. B.
C. D.
【解析】由图可得,如图所示的图案是由绕着一端旋转3次,每次旋转90°得到的,
选D.
命题角度六 求旋转对称图形的旋转角度
例题6.如图,香港特别行政区标志紫荆花图案绕中心旋转false°后能与原来的图案互相重合,则false的最小值为( )
A.45 B.60 C.72 D.144
【分析】该图形被平分成五部分,因而每部分被分成的圆心角是false,并且圆具有旋转不变性,因而旋转false的整数倍,就可以与自身重合.
【解析】该图形被平分成五部分,旋转false的整数倍,就可以与自身重合,故false的最小值为false.选false.
【小结】本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
变式1.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是( )
A.甲 B.乙 C.丙 D.丁
【解析】圆被平分成八部分,旋转45°的整数倍,就可以与自身重合,因而甲,丙,丁都正确;错误的是乙.选B.
变式2.如图是几种常见的汽车轮毂图案,图案围绕中心旋转90°后能与原来的图案重合的是( )
A. B. C. D.
【分析】
根据各选项图形以及旋转的概念即可逐一判断.
【解析】
A、此图形旋转60°或60°的整数倍能与原来的图案重合;
B、此图形旋转45°或45°的整数倍能与原来的图案重合;
C、此图形旋转72°或72°的整数倍能与原来的图案重合;
D、此图形旋转36°或36°的整数倍能与原来的图案重合;
故答案为:B.
【小结】
本题考查了旋转的概念,解题的关键是熟知旋转的概念.
10553700104267001264920011531600讲次0 2中心对称
中心对称概念:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫作对称中心.这两个图形旋转后能重合的对应点叫作关于对称中心的对称点.
如图,false绕着点false旋转false后,与false完全重合,则称false和false关于点false对称,点false是点false关于点false的对称点.
中心对称图形概念:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫作中心对称图形,这个点就是它的对称中心.
中心对称与中心对称图形的区别与联系:
中心对称
中心对称图形
区别
(1)是针对两个图形而言的.
(2)是指两个图形的(位置)关系.
(3)对称点在两个图形上.
(4)对称中心在两个图形之间.
(1)是针对一个图形而言的.
(2)是指具有某种性质的一个图形.
(3)对称点在一个图形上.
(4)对称中心在图形上.
联系
(1)都是通过把图形旋转180°重合来定义的.
(2)两者可以相互转化,如果把中心对称的两个图形看成一个整体(一个图形),那么这“一个图形”就是中心对称图形;反过来,如果把一个中心对称图形相互对称的两部分看成两个图形,那么这“两个图形”中心对称
中心对称的性质:
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
2.中心对称的两个图形是全等图形.
找对称中心的方法和步骤:
方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.
方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
关于原点对称的点的坐标规律
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点
P’(-x,-y)
命题角度一 中心对称图形的识别
例题1.下列图形中,既是轴对称图形又是中心对称图形的是false false
A. B. C. D.
【解析】
A. 是轴对称图形,但不是中心对称图形,故不符合题意;
B. 不是轴对称图形,是中心对称图形,故不符合题意;
C. 是轴对称图形,但不是中心对称图形,故不符合题意;
D. 既是轴对称图形又是中心对称图形,故符合题意.
选D.
变式1.下列图形中,是中心对称图形的是( )
A. B. C. D.
【解析】
A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项正确;
选D.
变式2.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解析】A.是轴对称图形,不是中心对称图形;
B.是轴对称图形,也是中心对称图形;
C.是轴对称图形,不是中心对称图形;
D.是轴对称图形,不是中心对称图形.
选B.
变式3.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
【解析】A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,不是中心对称图形,故不符合题意;
C、是轴对称图形,也是中心对称图形,故符合题意;
D、是轴对称图形,不是中心对称图形,故不符合题意,
选C.
命题角度二 判断中心对称图形的对称中心
例题2.如图,已知图形是中心对称图形,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
【解析】∵此图形是中心对称图形,∴对称中心是线段FC的中点。
选D.
变式1.如图所示的中心对称图形中,对称中心是( )
A.false B.false C.false D.false
【解析】
如图所示的中心对称图形中,对称中心是O2.
选B.
变式2.如图,将false绕点false旋转false得到false设点false的坐标为false, 则点false的坐标为( )
A.false B.false
C.false D.false
【分析】
根据旋转变换的对应点关于旋转中心对称,再根据中点公式列式求解即可.
【解析】
根据题意,点A、A′关于点C对称,
设点A’的坐标是(x,y),
则false,false,解得x=?a+2,y=?b+2,
∴点A’的坐标是false.
选C.
【小结】
本题考查了利用旋转进行坐标与图形的变化,根据旋转的性质得出点A、A′关于点C成中心对称是解题的关键,还需注意中点公式的利用,也是容易出错的地方.
命题角度三 中心对称的性质
例题3.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点false是对称点 B.false C.false D.false
【解析】
A、正确;
B、正确;
C、根据OA=OA′,OB=OB′,∠AOB=∠A′OB′,得到△AOB≌△A′OB′.则∠ABO=∠A′B′O,则AB∥A′B′,正确;
D、两个角不是对应角,错误.
选D.
变式1.如图是一个以O为对称中心的中心对称图形,若∠A=30°, ∠C=90°,OC=1,则AB的长为( )
A.2 B.4 C.false D.false
【解析】由中心对称图形的性质,可得:AO=BO,
∴AB=2OA,
在Rt△AOC中,
∠A=30°, ∠C=90°,OC=1,
∴OA=2OC=2,∴ AB=4.
选B.
变式2.如图所示,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是( )
A.AB=A′B′,BC=B′C′ B.AB∥A′B′,BC∥B′C′
C.S△ABC=S△A′B′C′ D.△ABC≌△A′OC′
【分析】根据成中心对称图形的性质:对应边平行且相等,对应角相等,图形全等,面积相等进行判断.
【解析】∵△ABC与△A′BC′是成中心对称的两个图形,
∴AB=A′B′,BC=B′C′,AB∥A′B′,BC∥B′C′,S△ABC=S△A′B′C′,
无法得到:△ABC≌△A′OC′.所以选D.
变式3.如图,false与false关于false成中心对称,下列结论中不一定成立的是( )
A.false B.false
C.false D.false
【分析】根据中心对称性质逐个提示即可.
【解析】A. false,本选项不一定正确;
B. false,对应边相等;
C. false,对应边相等;
D. false,对应边相等;
选A
【小结】考核知识点:中心对称性质.理解中心对称的基本性质是关键.
命题角度四 根据中心对称的性质求面积
例题4.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
【解析】由图形可知,长方形的面积=10×4=40cm2,再根据中心对称的性质得,图中阴影部分的面积即是长方形面积的一半,则图中阴影部分的面积=false×40=20cm2,选A.
变式1.用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都正确 D.甲、乙都不正确
【解析】如图:图形2中,直线m经过了大长方形和小长方形的对角线的交点,所以两旁的图形的面积都是大长方形和小长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即甲做法正确;
图形3中,经过大正方形和图形外不添补的长方形的对角线的交点,直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即乙做法正确.
选C.
变式2.如图,在面积为12的□ABCD中,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交AB、CD于点E、F,若AE=2EB,则图中阴影部分的面积等于( )
A.3 B.1 C.false D.false
【解析】
∵□ABCD,
∴AO=OC,∠CAB=∠DCO.
∵在△AOE和△COF中AO=OC,∠CAB=∠DCO,∠AOE=∠COF.
∴△AOE≌△COF.
∴S△FCO=S△OAE.
∵面积为12的□ABCD,
∴S△DAB=6.
过点D做DG⊥AB,OH⊥AB,
∵O为中点,
∴OH=falseDG.
∴S阴影=SOAB=false S△DAB=3.
选A.
【小结】本题考查的是平行四边形,熟练掌握平行四边形的性质是解题的关键.
命题角度五 在方格纸中补画图形使之成为中心对称图形
例题5.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
【解析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,通过观察发现,当涂黑②时,所形成的图形关于点A中心对称。选B。
变式1.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
【解析】
利用轴对称图形的性质以及中心对称图形的性质提示得出符合题意的图形即可.如图所示:组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
选C.
变式2.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中涂色部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
【分析】根据中心对称图形的概念,如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形.将④涂黑后,与图中阴影部分构成的图形绕第三个正方形的中心旋转180°后,这个图形能与自身重合,是中心对称图.
【解析】将④涂黑后,与图中阴影部分构成的图形绕第三个正方形的中心旋转180°后,这个图形能与自身重合,是中心对称图.
选D.
【小结】本题考查的是利用旋转设计图案,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
命题角度六 关于原点对称的点的坐标
例题6.在平面直角坐标系中,点false关于原点对称的点的坐标是( )
A.false B.false C.false D.false
【解析】点P(-3,-5)关于原点对称的点的坐标是(3,5),
选C.
变式1.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为()
A.33 B.-33 C.-7 D.7
【解析】关于原点对称的两个点,横坐标和纵坐标分别互为相反数.根据性质可得:a=-13,b=20,则a+b=-13+20=7.
变式2.在平面直角坐标系中,点false关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解析】∵false,∴点false在第二象限,
∴点false关于原点对称点在第四象限.
选D.
变式3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则yx的值是( )
A.2 B.false C.4 D.8
【解析】∵点A(x,y-4)与点B(1-y,2x)关于原点对称,
∴false 解得:false 则yx=2-1=false.
选B.
变式4.若在平面直角坐标系内A(m-1,6),B(-2,n)两点关于原点对称,则m+n的值为( )
A.9 B.-3 C.3 D.5
【解析】∵在平面直角坐标系内A(m-1,6),B(-2,n)两点关于原点对称,
∴m-1+(-2)=0,6+n=0,
∴m=3,n=-6,
∴m+n=3+(-6)=-3.
选B.
同课章节目录
