冀教版数学七年级下册第九章三角形达标测试卷(word含答案)
文档属性
| 名称 | 冀教版数学七年级下册第九章三角形达标测试卷(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 17:06:05 | ||
图片预览




文档简介
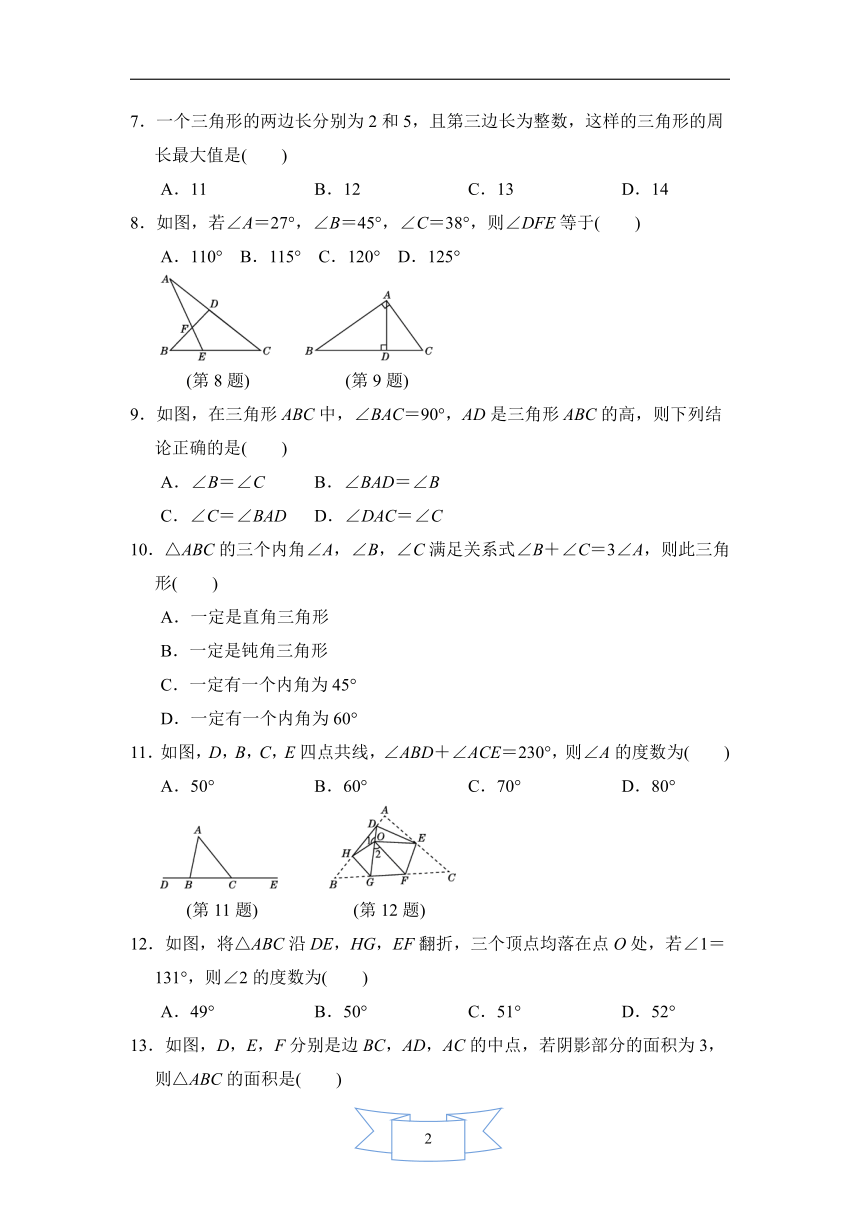
第九章达标测 试卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列各组中的三条线段(单位:cm),能围成三角形的是( )
A.1,2,3 B.2,3,4
C.10,20,35 D.4,4,9
2.如图,在△ABC中,AD平分∠BAC,∠C=30°,∠DAC=45°,则∠B的度数为( )
A.60° B.65° C.70° D.75°
(第2题) (第3题) (第4题)
3.如图,为了估计一池塘岸边两点A,B之间的距离,小颖同学在池塘一侧选取了一点P,测得PA=100 m, PB=90 m,那么点A与点B之间的距离不可能是( )
A.90 m B.100 m C.150 m D.190 m
4.如图,在△ABC中,AD为BC边上的中线,DE为△ABD中AB边上的中线,△ABC的面积为6,则△ADE的面积是( )
A.1 B. C.2 D.
5.将一副直角三角尺按如图所示方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边重合,则∠1的度数为( )
A.45° B.65° C.70° D.75°
(第5题) (第6题)
6.如图所示,AC⊥BC于C,CD⊥AB于D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
7.一个三角形的两边长分别为2和5,且第三边长为整数,这样的三角形的周长最大值是( )
A.11 B.12 C.13 D.14
8.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A.110° B.115° C.120° D.125°
(第8题) (第9题)
9.如图,在三角形ABC中,∠BAC=90°,AD是三角形ABC的高,则下列结论正确的是( )
A.∠B=∠C B.∠BAD=∠B
C.∠C=∠BAD D.∠DAC=∠C
10.△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=3∠A,则此三角形( )
A.一定是直角三角形
B.一定是钝角三角形
C.一定有一个内角为45°
D.一定有一个内角为60°
11.如图,D,B,C,E四点共线,∠ABD+∠ACE=230°,则∠A的度数为( )
A.50° B.60° C.70° D.80°
(第11题) (第12题)
12.如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
13.如图,D,E,F分别是边BC,AD,AC的中点,若阴影部分的面积为3,则△ABC的面积是( )
A.5 B.6 C.7 D.8
(第13题) (第14题)
14.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
15.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
(第15题) (第16题)
16.如图,△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(17题3分,其余每空2分,共11分)
17.如图,∠BDC=130°,∠A=40°,∠B+∠C的大小是________.
(第17题) (第18题) (第19题)
18.如图,在△ABC中,∠ABC,∠ACB的平分线BO,CO交于点O,CE为△ABC的外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2=α,则∠1=______,∠BOC=______(用含α的式子表示).
19.如图,△ABC中,∠ABC>90°,AD,CE,BF分别是△ABC的高,AB=5,BC=4,高AD,CE,BF的大小关系是________________,若AD=3,则CE=________.
三、解答题(20题8分,21~23题每题9分,24~25题每题10分,26题12分,共67分)
20.补充下列解题过程,并在括号内填上推理依据.
已知:如图,在△ABC中,∠A=50°,∠C=58°,BD平分∠ABC交AC于点D,DE交AB于点E,且∠BDE=36°.试说明:DE∥BC.
解:∵∠A+∠C+∠ABC=180°( ),
∠A=50°,∠C=58°,
(第20题)
∴50°+58°+∠ABC=180°.( )
∴∠ABC=180°-50°-________=________.
∵BD平分∠ABC,
∴∠CBD=∠ABC=36°.( )
∵∠BDE=36°,∴________=________.
∴BC∥DE.( )
21.在△ABC中,∠A+∠B=∠C,∠B-∠A=30°.
(1)求∠A,∠B,∠C的度数;
(2)△ABC按角分类,属于什么三角形?△ABC按边分类,属于什么三角形?
22.观察并探求下列各问题.
(1)如图①,在△ABC中,P为边BC上一点,则BP+PC________AB+AC(填“>”“<”或“=”).
(2)将(1)中点P移到△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)将(2)中点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
(第22题)
23.探究与发现:如图①,有一块直角三角尺DEF放置在△ABC上,三角尺DEF的两条直角边DE,DF恰好分别经过点B,C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用:某零件如图②所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°时,就断定这个零件不合格,你能说出其中的道理吗?
(第23题)
24.如图,在△ABC中,∠B<∠ACB,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当点P在线段AD上运动时,试说明:∠E=(∠ACB-∠B).
(第24题)
25.如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数;
(2)若∠PEF=75°,2∠CFQ=∠PFC,求∠EFP的度数.
(第25题
26.探究与发现:如图①所示的图形,像我们常见的学习用品——圆规,我们不妨把这样的图形叫做“规形图”.
(1)观察“规形图①”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决问题:
如图②,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
(第26题)
答案
一、1.B 2.A 3.D 4.B 5.D 6.D
7.C 8.A 9.C 10.C 11.A 12.A
13.D 14.C 15.C
16.C 【点拨】①因为EG∥BC,
所以∠CEG=∠ACB.
又因为CD是△ABC的角平分线,
所以∠ACD=∠BCD,
所以∠CEG=∠ACB=2∠DCB,故①正确;
②因为∠CEG=∠ACB,而∠GEC与∠GCE不一定相等,
所以CA不一定平分∠BCG,故②错误;
③因为∠A=90°,
所以∠ADC+∠ACD=90°.
因为CD平分∠ACB,
所以∠ACD=∠BCD.
所以∠ADC+∠BCD=90°.
因为EG∥BC,且CG⊥EG,
所以∠GCB=90°,即∠GCD+∠BCD=90°,
所以∠ADC=∠GCD,故③正确;
④因为∠A=90°,所以∠ABC+∠ACB=90°.
因为CD平分∠ACB,BE平分∠ABC,
所以∠EBC=∠ABC,∠DCB=∠ACB,
所以∠DFB=∠EBC+∠DCB=(∠ABC+∠ACB)=45°.
因为CG⊥EG,
所以∠CGE=90°,
所以∠DFB=∠CGE,
故④正确.故选C.
二、17.90° 18.2α;90°+α
19.BF且BC因为S△ABC=AB·CE=BC·AD,
所以CE===.
三、20.三角形内角和定理;等量代换;58°;72°;角平分线的定义;
∠CBD;∠BDE;内错角相等,两直线平行
21.解:(1)由题意得,
解得
(2)因为∠C=90°,∠A=30°,
∠B=60°,所以△ABC按角分类,属于直角三角形.△ABC按边分类,属于不等边三角形.
22.解:(1)<
(2)△BPC的周长<△ABC的周长.理由: 如图①,延长BP交AC于M,在△ABM中,BP+PM在△PMC中,PC(3)四边形BP1P2C的周长<△ABC的周长.
理由:如图②,分别延长BP1,CP2交于点M,由(2)知,BM+CM所以BP1+P1P2+P2C(第22题)
23.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD.
理由如下:因为∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
所以∠BDC=∠A+∠ABD+∠ACD.
应用:
由上述结论得∠BDC=∠A+∠ABD+∠ACD=143°.
因为检验员量得∠BDC=145°≠143°,
所以这个零件不合格.
24.解:(1)因为∠B=35°,∠ACB=85°,
所以∠BAC=180°-∠B-∠ACB=60°.
因为AD平分∠BAC,
所以∠DAC=∠BAD=30°.
所以∠ADC=∠B+∠BAD=65°.
因为PE⊥PD,所以∠DPE=90°,
所以∠E=180°-∠DPE-∠ADC=25° .
(2)因为∠B+∠BAC+∠ACB=180°,
所以∠BAC=180°-(∠B+∠ACB).
因为AD平分∠BAC,
所以∠BAD=∠BAC=90°-(∠B+∠ACB).
所以∠ADC=∠B+∠BAD=90°-(∠ACB-∠B).
因为PE⊥AD,所以∠DPE=90°.
所以∠ADC+∠E=180°-90°=90°.
所以∠E=90°-∠ADC,
即∠E=(∠ACB-∠B).
25.解:(1)∠EFP的度数为42°或66°.
(2)①当点Q在平行线AB,CD之间时,因为AB∥CD,
所以∠EFD=∠PEF=75°.
设∠PFQ=x,由折叠可知∠EFP=x,
因为2∠CFQ=∠CFP,
所以∠PFQ=∠CFQ=x,
所以75°+3x=180°,
所以x=35°,所以∠EFP=35°.
②当点Q在CD下方时,
设∠PFQ=y,由折叠可知∠EFP=y,
因为2∠CFQ=∠CFP,
所以∠PFC=y,
所以75°+y+y=180°,
解得y=63°,
所以∠EFP=63°.
综上所述,∠EFP的度数为35°或63°.
26.解:(1)∠BDC=∠BAC+∠B+∠C,
理由:如图,过点A,D作射线AF,
因为∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
所以∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C.
(2)因为∠DAE=40°,∠DBE=130°,
所以∠ADB+∠AEB=130°-40°=90°.
因为DC平分∠ADB,EC平分∠AEB,
所以∠ADC=∠ADB,∠AEC=∠AEB,
所以∠ADC+∠AEC=(∠ADB+∠AEB)=45°,
所以∠DCE=∠DAE+∠ADC+∠AEC=40°+45°=85°.
(第26题)
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列各组中的三条线段(单位:cm),能围成三角形的是( )
A.1,2,3 B.2,3,4
C.10,20,35 D.4,4,9
2.如图,在△ABC中,AD平分∠BAC,∠C=30°,∠DAC=45°,则∠B的度数为( )
A.60° B.65° C.70° D.75°
(第2题) (第3题) (第4题)
3.如图,为了估计一池塘岸边两点A,B之间的距离,小颖同学在池塘一侧选取了一点P,测得PA=100 m, PB=90 m,那么点A与点B之间的距离不可能是( )
A.90 m B.100 m C.150 m D.190 m
4.如图,在△ABC中,AD为BC边上的中线,DE为△ABD中AB边上的中线,△ABC的面积为6,则△ADE的面积是( )
A.1 B. C.2 D.
5.将一副直角三角尺按如图所示方式放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边重合,则∠1的度数为( )
A.45° B.65° C.70° D.75°
(第5题) (第6题)
6.如图所示,AC⊥BC于C,CD⊥AB于D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
7.一个三角形的两边长分别为2和5,且第三边长为整数,这样的三角形的周长最大值是( )
A.11 B.12 C.13 D.14
8.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A.110° B.115° C.120° D.125°
(第8题) (第9题)
9.如图,在三角形ABC中,∠BAC=90°,AD是三角形ABC的高,则下列结论正确的是( )
A.∠B=∠C B.∠BAD=∠B
C.∠C=∠BAD D.∠DAC=∠C
10.△ABC的三个内角∠A,∠B,∠C满足关系式∠B+∠C=3∠A,则此三角形( )
A.一定是直角三角形
B.一定是钝角三角形
C.一定有一个内角为45°
D.一定有一个内角为60°
11.如图,D,B,C,E四点共线,∠ABD+∠ACE=230°,则∠A的度数为( )
A.50° B.60° C.70° D.80°
(第11题) (第12题)
12.如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
13.如图,D,E,F分别是边BC,AD,AC的中点,若阴影部分的面积为3,则△ABC的面积是( )
A.5 B.6 C.7 D.8
(第13题) (第14题)
14.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
15.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
(第15题) (第16题)
16.如图,△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(17题3分,其余每空2分,共11分)
17.如图,∠BDC=130°,∠A=40°,∠B+∠C的大小是________.
(第17题) (第18题) (第19题)
18.如图,在△ABC中,∠ABC,∠ACB的平分线BO,CO交于点O,CE为△ABC的外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2=α,则∠1=______,∠BOC=______(用含α的式子表示).
19.如图,△ABC中,∠ABC>90°,AD,CE,BF分别是△ABC的高,AB=5,BC=4,高AD,CE,BF的大小关系是________________,若AD=3,则CE=________.
三、解答题(20题8分,21~23题每题9分,24~25题每题10分,26题12分,共67分)
20.补充下列解题过程,并在括号内填上推理依据.
已知:如图,在△ABC中,∠A=50°,∠C=58°,BD平分∠ABC交AC于点D,DE交AB于点E,且∠BDE=36°.试说明:DE∥BC.
解:∵∠A+∠C+∠ABC=180°( ),
∠A=50°,∠C=58°,
(第20题)
∴50°+58°+∠ABC=180°.( )
∴∠ABC=180°-50°-________=________.
∵BD平分∠ABC,
∴∠CBD=∠ABC=36°.( )
∵∠BDE=36°,∴________=________.
∴BC∥DE.( )
21.在△ABC中,∠A+∠B=∠C,∠B-∠A=30°.
(1)求∠A,∠B,∠C的度数;
(2)△ABC按角分类,属于什么三角形?△ABC按边分类,属于什么三角形?
22.观察并探求下列各问题.
(1)如图①,在△ABC中,P为边BC上一点,则BP+PC________AB+AC(填“>”“<”或“=”).
(2)将(1)中点P移到△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)将(2)中点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
(第22题)
23.探究与发现:如图①,有一块直角三角尺DEF放置在△ABC上,三角尺DEF的两条直角边DE,DF恰好分别经过点B,C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用:某零件如图②所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°时,就断定这个零件不合格,你能说出其中的道理吗?
(第23题)
24.如图,在△ABC中,∠B<∠ACB,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当点P在线段AD上运动时,试说明:∠E=(∠ACB-∠B).
(第24题)
25.如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数;
(2)若∠PEF=75°,2∠CFQ=∠PFC,求∠EFP的度数.
(第25题
26.探究与发现:如图①所示的图形,像我们常见的学习用品——圆规,我们不妨把这样的图形叫做“规形图”.
(1)观察“规形图①”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决问题:
如图②,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
(第26题)
答案
一、1.B 2.A 3.D 4.B 5.D 6.D
7.C 8.A 9.C 10.C 11.A 12.A
13.D 14.C 15.C
16.C 【点拨】①因为EG∥BC,
所以∠CEG=∠ACB.
又因为CD是△ABC的角平分线,
所以∠ACD=∠BCD,
所以∠CEG=∠ACB=2∠DCB,故①正确;
②因为∠CEG=∠ACB,而∠GEC与∠GCE不一定相等,
所以CA不一定平分∠BCG,故②错误;
③因为∠A=90°,
所以∠ADC+∠ACD=90°.
因为CD平分∠ACB,
所以∠ACD=∠BCD.
所以∠ADC+∠BCD=90°.
因为EG∥BC,且CG⊥EG,
所以∠GCB=90°,即∠GCD+∠BCD=90°,
所以∠ADC=∠GCD,故③正确;
④因为∠A=90°,所以∠ABC+∠ACB=90°.
因为CD平分∠ACB,BE平分∠ABC,
所以∠EBC=∠ABC,∠DCB=∠ACB,
所以∠DFB=∠EBC+∠DCB=(∠ABC+∠ACB)=45°.
因为CG⊥EG,
所以∠CGE=90°,
所以∠DFB=∠CGE,
故④正确.故选C.
二、17.90° 18.2α;90°+α
19.BF
所以CE===.
三、20.三角形内角和定理;等量代换;58°;72°;角平分线的定义;
∠CBD;∠BDE;内错角相等,两直线平行
21.解:(1)由题意得,
解得
(2)因为∠C=90°,∠A=30°,
∠B=60°,所以△ABC按角分类,属于直角三角形.△ABC按边分类,属于不等边三角形.
22.解:(1)<
(2)△BPC的周长<△ABC的周长.理由: 如图①,延长BP交AC于M,在△ABM中,BP+PM
理由:如图②,分别延长BP1,CP2交于点M,由(2)知,BM+CM
23.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD.
理由如下:因为∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
所以∠BDC=∠A+∠ABD+∠ACD.
应用:
由上述结论得∠BDC=∠A+∠ABD+∠ACD=143°.
因为检验员量得∠BDC=145°≠143°,
所以这个零件不合格.
24.解:(1)因为∠B=35°,∠ACB=85°,
所以∠BAC=180°-∠B-∠ACB=60°.
因为AD平分∠BAC,
所以∠DAC=∠BAD=30°.
所以∠ADC=∠B+∠BAD=65°.
因为PE⊥PD,所以∠DPE=90°,
所以∠E=180°-∠DPE-∠ADC=25° .
(2)因为∠B+∠BAC+∠ACB=180°,
所以∠BAC=180°-(∠B+∠ACB).
因为AD平分∠BAC,
所以∠BAD=∠BAC=90°-(∠B+∠ACB).
所以∠ADC=∠B+∠BAD=90°-(∠ACB-∠B).
因为PE⊥AD,所以∠DPE=90°.
所以∠ADC+∠E=180°-90°=90°.
所以∠E=90°-∠ADC,
即∠E=(∠ACB-∠B).
25.解:(1)∠EFP的度数为42°或66°.
(2)①当点Q在平行线AB,CD之间时,因为AB∥CD,
所以∠EFD=∠PEF=75°.
设∠PFQ=x,由折叠可知∠EFP=x,
因为2∠CFQ=∠CFP,
所以∠PFQ=∠CFQ=x,
所以75°+3x=180°,
所以x=35°,所以∠EFP=35°.
②当点Q在CD下方时,
设∠PFQ=y,由折叠可知∠EFP=y,
因为2∠CFQ=∠CFP,
所以∠PFC=y,
所以75°+y+y=180°,
解得y=63°,
所以∠EFP=63°.
综上所述,∠EFP的度数为35°或63°.
26.解:(1)∠BDC=∠BAC+∠B+∠C,
理由:如图,过点A,D作射线AF,
因为∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
所以∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C.
(2)因为∠DAE=40°,∠DBE=130°,
所以∠ADB+∠AEB=130°-40°=90°.
因为DC平分∠ADB,EC平分∠AEB,
所以∠ADC=∠ADB,∠AEC=∠AEB,
所以∠ADC+∠AEC=(∠ADB+∠AEB)=45°,
所以∠DCE=∠DAE+∠ADC+∠AEC=40°+45°=85°.
(第26题)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
