江苏盐城2021年中考备战策略(14)《函数及其图象》专题强化提优
文档属性
| 名称 | 江苏盐城2021年中考备战策略(14)《函数及其图象》专题强化提优 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
江苏盐城2021年中考备战策略(14)《函数及其图象》专题强化提优
知识点扫描
考点一函数的概念和函数的图象
1.函数的概念
(1)在一个变化过程中,我们称数值___________的量为变量,有些数值_____________的,称它们为常量.
(2)一般地,在一个变化过程中,如果有两个变量x与y,并且对于x在其取值范围内的每一个确定的值,y都有_________的值与其对应,那么就说,x是_______,y是x的函数.
(3)用来表示函数关系的数学式子,叫做函数解析式或函数关系式.
2.函数的表示法及自变量的取值范围
(1)函数有三种表示方法:_________,_________,_______,这三种方法有时可以互相转化.
(2)当函数解析式表示实际问题或几何问题时,其自变量的取值范围必须符合实际意义或几何意义.
3.函数的图象:对于一个函数,把自变量x和函数y的每对对应值分别作为点的_______,
_________在平面内描出相应的点,组成这些点的图形叫这个函数的图象.
(1)画函数图象,一般按下列步骤进行:列表、描点、连线.
(2)图象上任一点的坐标是解析式方程的一个解;反之以解析式方程的任意一个解为坐标的点一定在函数图象上.
求函数自变量的取值范围时,首先要考虑自变量的取值必须使解析式有意义.
1.自变量以整式形式出现,它的取值范围是全体实数.
2.自变量以分式形式出现,它的取值范围是使分母不为零的实数.
3.当自变量以偶次方根形式出现,它的取值范围是使被开方数为非负数;以奇次方根出现时,它的取值范围为全体实数.
4.当自变量出现在零次幂或负整数幂的底数中,它的取值范围是使底数不为零的数.
5.在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
经典例题
例1.(1)函数y=的自变量x的取值范围是________.
(2)在函数y=中,自变量x的取值范围是________.
(3)函数y=的自变量x的取值范围是________.
(4)函数y=中自变量x的取值范围是________.
(1)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象.若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
(2)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
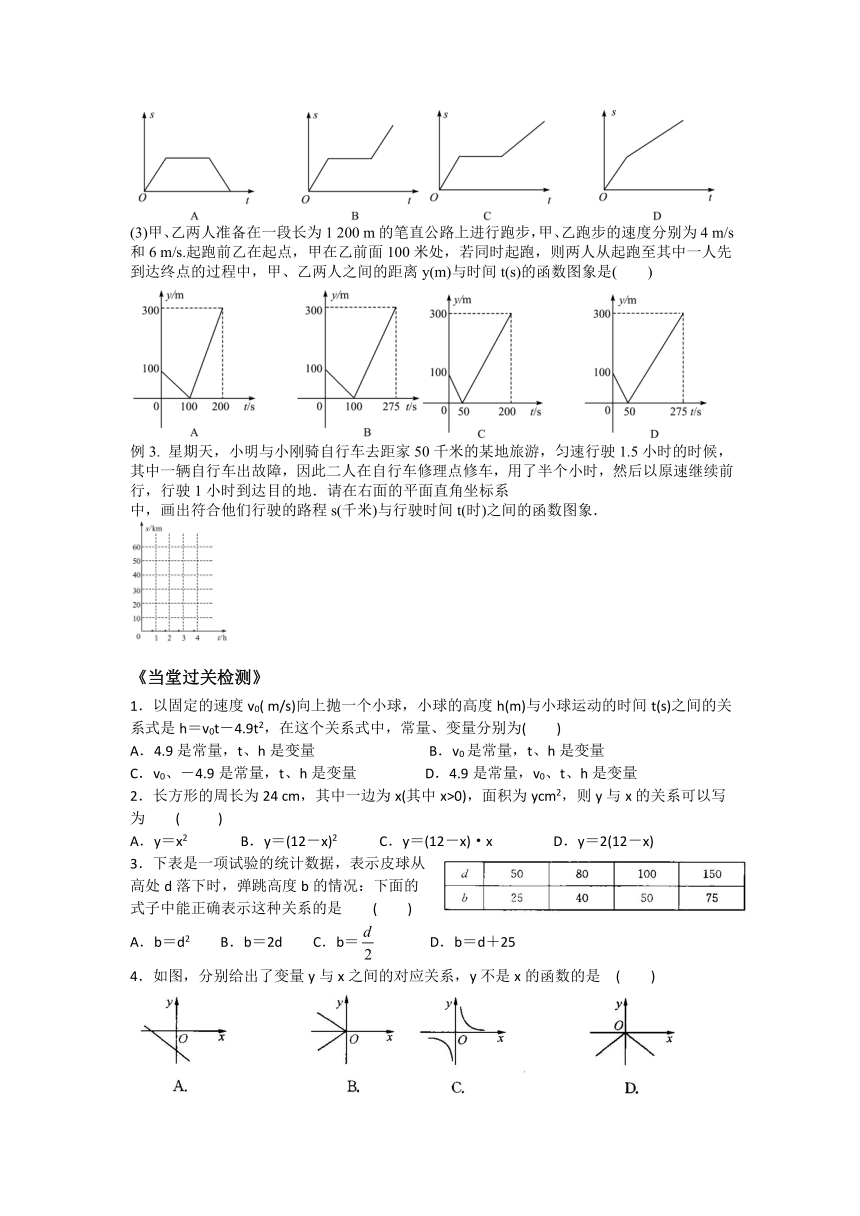
(3)甲、乙两人准备在一段长为1 200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s.起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是( )
星期天,小明与小刚骑自行车去距家50千米的某地旅游,匀速行驶1.5小时的时候,其中一辆自行车出故障,因此二人在自行车修理点修车,用了半个小时,然后以原速继续前行,行驶1小时到达目的地.请在右面的平面直角坐标系
中,画出符合他们行驶的路程s(千米)与行驶时间t(时)之间的函数图象.
《当堂过关检测》
1.以固定的速度v0( m/s)向上抛一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量 B.v0是常量,t、h是变量
C.v0、-4.9是常量,t、h是变量 D.4.9是常量,v0、t、h是变量
2.长方形的周长为24 cm,其中一边为x(其中x>0),面积为ycm2,则y与x的关系可以写为 ( )
A.y=x2 B.y=(12-x)2 C.y=(12-x)·x D.y=2(12-x)
3.下表是一项试验的统计数据,表示皮球从高处d落下时,弹跳高度b的情况:下面的式子中能正确表示这种关系的是 ( ) A.b=d2 B.b=2d C.b= D.b=d+25
4.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( )
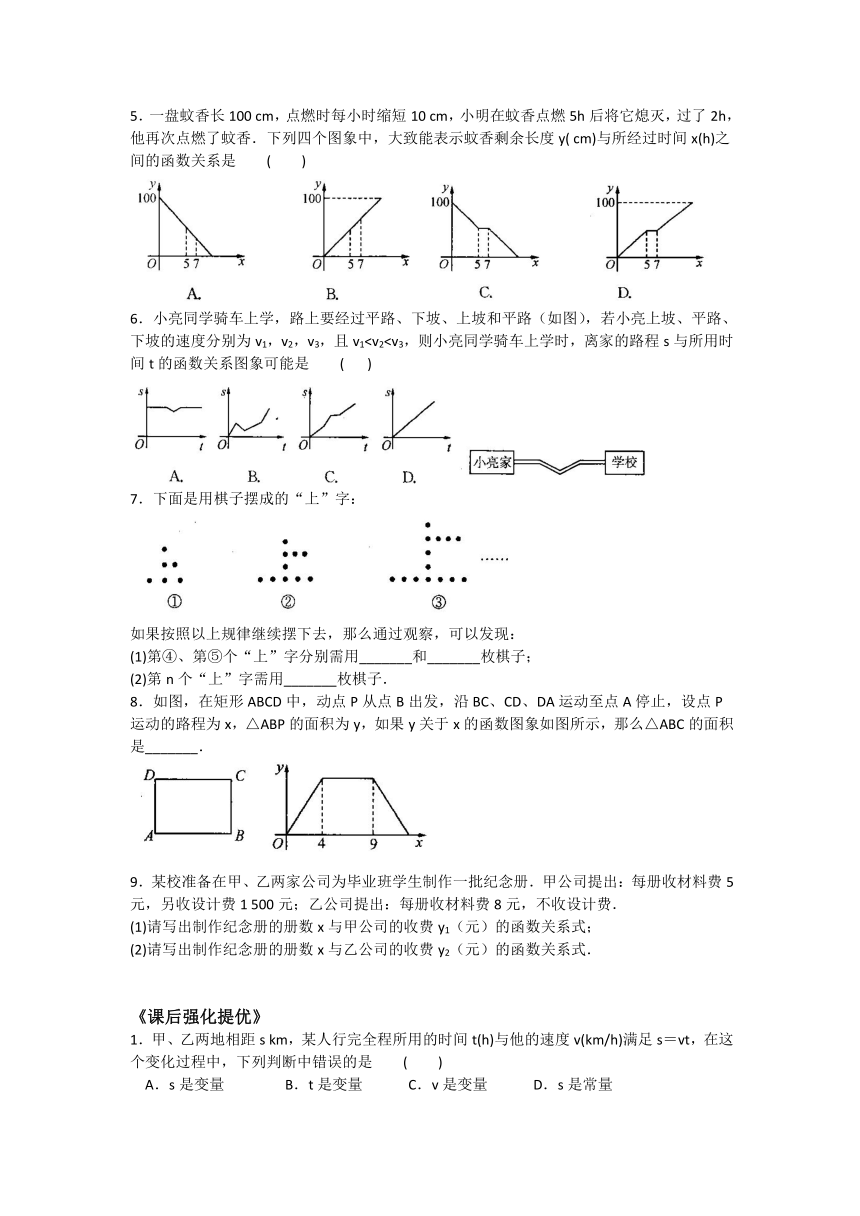
5.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y( cm)与所经过时间x(h)之间的函数关系是 ( )
6.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,且v17.下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第④、第⑤个“上”字分别需用_______和_______枚棋子;
(2)第n个“上”字需用_______枚棋子.
8.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积是_______.
9.某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数x与甲公司的收费y1(元)的函数关系式;
(2)请写出制作纪念册的册数x与乙公司的收费y2(元)的函数关系式.
《课后强化提优》
1.甲、乙两地相距s km,某人行完全程所用的时间t(h)与他的速度v(km/h)满足s=vt,在这个变化过程中,下列判断中错误的是 ( )
A.s是变量 B.t是变量 C.v是变量 D.s是常量
2.在圆周长公式C=2πr中,变量是 ( )
A.C、2、π、r B.C、π、r C.C、r D. r
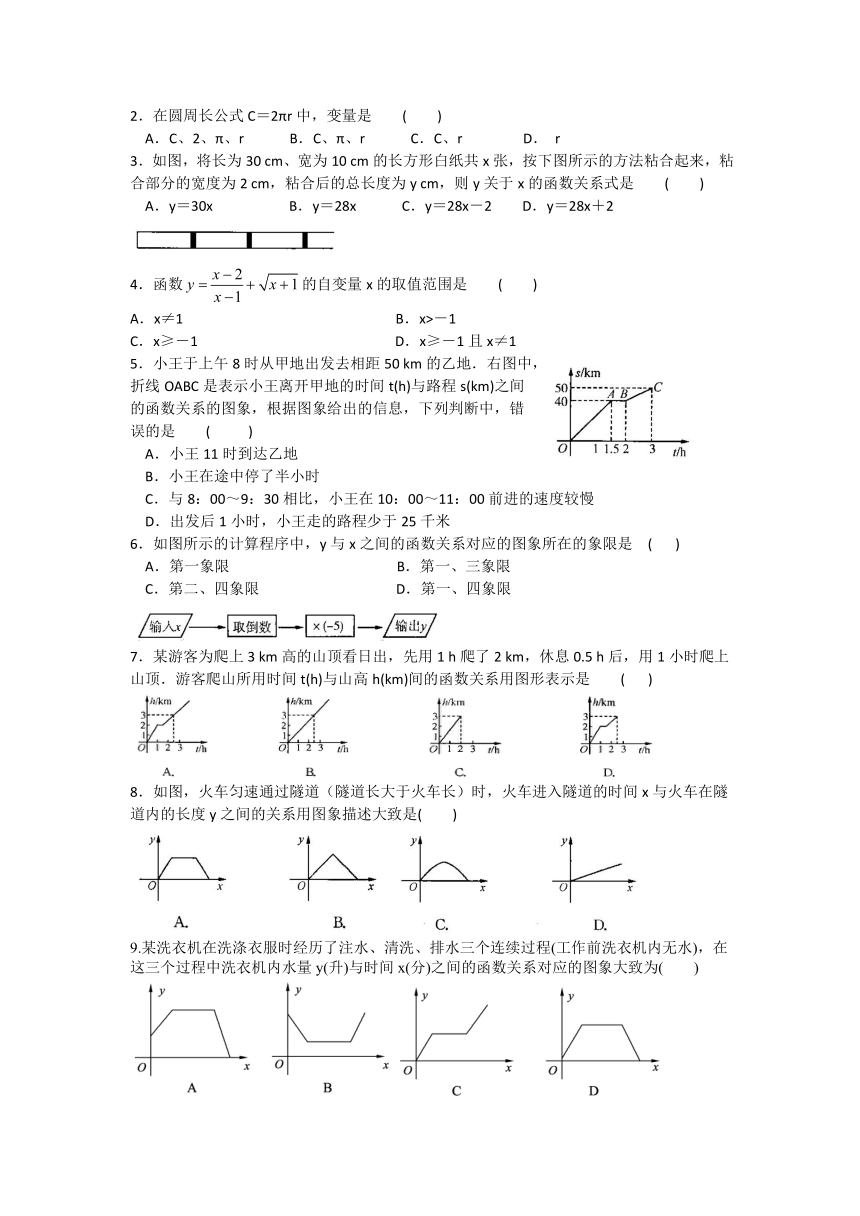
3.如图,将长为30 cm、宽为10 cm的长方形白纸共x张,按下图所示的方法粘合起来,粘合部分的宽度为2 cm,粘合后的总长度为y cm,则y关于x的函数关系式是 ( )
A.y=30x B.y=28x C.y=28x-2 D.y=28x+2
4.函数的自变量x的取值范围是 ( )
A.x≠1 B.x>-1
C.x≥-1 D.x≥-1且x≠1
5.小王于上午8时从甲地出发去相距50 km的乙地.右图中,
折线OABC是表示小王离开甲地的时间t(h)与路程s(km)之间
的函数关系的图象,根据图象给出的信息,下列判断中,错
误的是 ( )
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8:00~9:30相比,小王在10:00~11:00前进的速度较慢
D.出发后1小时,小王走的路程少于25千米
6.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 ( )
A.第一象限 B.第一、三象限
C.第二、四象限 D.第一、四象限
7.某游客为爬上3 km高的山顶看日出,先用1 h爬了2 km,休息0.5 h后,用1小时爬上山顶.游客爬山所用时间t(h)与山高h(km)间的函数关系用图形表示是 ( )
8.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
10.一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( )
A.摩托车比汽车晚到1 h
B.A、B两地的路程为20 km
C.摩托车的速度为45 km/h
D.汽车的速度为60 km/h
11.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是_______,自变量x的取值范围是_______
12.到邮局投寄平信,每封信的质量不超过20 g时付邮费0. 80元,超过20 g而不超过40 g时付邮费1.60元……依此类推,每增加20 g需增加邮费0.80元(信的质量在100 g内).如果某人投寄一封信的质量为78.5 g,则他应付邮费_______元.
13.打字收费标准是每千字5元,打字费m(元)与字数a(个)的函数关系式为_______,自变量a的取值范围是_______.
某种储蓄的年利率为3.25%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为_______;4年后的本息和为_______元.
15如右图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象,根据图象提供的信息,可知该公路的长度是________米.
16.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明往返的平均速度为________km/h.
17.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离开家的距离与时间的关系可用图中的折线表示.
根据图象回答下列问题:
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时至13时,他们走了多少千米?
返回时,他们的平均速度是多少?
18.某单位计划与某个体车主或某国营出租车公司中的一家签定月租车合同.设汽车每月行驶x千米,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元.在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
(1)当每月行驶的路程不足1 500千米时,租哪家车合算?
(2)当每月行驶的路程为多少时,租两家车的费用相同?
(3)如果估计每月行驶的路程为2 300千米,租用哪家的车合算?
19.小亮步行从家去书店,用一段时间选择自己需要的书籍,然后回家.小亮和家的距离与他离开家以后的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)小亮用多少时间走到书店?小亮家距书店多远?
(2)小亮在书店停留了多长时间?回家用了多少时间?
(3)小亮去书店和回家的步行速度各是多少?
(4)小亮从家里走出10分钟时离家多远?走出50分钟时离家多远?
教师样卷
知识点扫描
考点一函数的概念和函数的图象
1.函数的概念
(1)在一个变化过程中,我们称数值发生变化的量为变量,有些数值是始终不变的,称它们为常量.
(2)一般地,在一个变化过程中,如果有两个变量x与y,并且对于x在其取值范围内的每一个确定的值,y都有唯一确定的值与其对应,那么就说,x是自变量,y是x的函数.
(3)用来表示函数关系的数学式子,叫做函数解析式或函数关系式.
2.函数的表示法及自变量的取值范围
(1)函数有三种表示方法:解析法,列表法,图象法,这三种方法有时可以互相转化.
(2)当函数解析式表示实际问题或几何问题时,其自变量的取值范围必须符合实际意义或几何意义.
3.函数的图象:对于一个函数,把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标在平面内描出相应的点,组成这些点的图形叫这个函数的图象.
(1)画函数图象,一般按下列步骤进行:列表、描点、连线.
(2)图象上任一点的坐标是解析式方程的一个解;反之以解析式方程的任意一个解为坐标的点一定在函数图象上.
求函数自变量的取值范围时,首先要考虑自变量的取值必须使解析式有意义.
1.自变量以整式形式出现,它的取值范围是全体实数.
2.自变量以分式形式出现,它的取值范围是使分母不为零的实数.
3.当自变量以偶次方根形式出现,它的取值范围是使被开方数为非负数;以奇次方根出现时,它的取值范围为全体实数.
4.当自变量出现在零次幂或负整数幂的底数中,它的取值范围是使底数不为零的数.
5.在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
经典例题
例1.(1)函数y=的自变量x的取值范围是________.
(2)在函数y=中,自变量x的取值范围是________.
(3)函数y=的自变量x的取值范围是________.
(4)函数y=中自变量x的取值范围是________.
【解答】(1)由x-2≠0得x≠2.
(2)由x+4≥0,得x≥-4.
(3)由得x≥3.
(4)由x+1>0,得x>-1.
(1)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象.若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
(2)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
(3)甲、乙两人准备在一段长为1 200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s.起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是( )
【解答】(1)由已知图可知,张老师出门散步可分为3个过程,首先离家越来越远,其次保持一段时间距离不变,最后返回家中,故选D.
(2)从甲地顺流航行到乙地,速度快;逆流航行时速度慢,故顺流航行的图象与x轴的夹角比逆流航行时与x轴的夹角大,图象大致是陡、平、缓,故选C.
(3)乙追上甲所用时间为100÷(6-4)=50(s),乙到达终点所用时间为1 200÷6=200(s),故选C.
星期天,小明与小刚骑自行车去距家50千米的某地旅游,匀速行驶1.5小时的时候,其中一辆自行车出故障,因此二人在自行车修理点修车,用了半个小时,然后以原速继续前行,行驶1小时到达目的地.请在右面的平面直角坐标系
中,画出符合他们行驶的路程s(千米)与行驶时间t(时)之间的函数图象.
【解答】
【点拨】由题意知,速度为50÷(1.5+1)=20(千米/时),20×1.5=30(千米),其中1.5小时~2.0小时s不变.
《当堂过关检测》
1.以固定的速度v0( m/s)向上抛一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( C)
A.4.9是常量,t、h是变量 B.v0是常量,t、h是变量
C.v0、-4.9是常量,t、h是变量 D.4.9是常量,v0、t、h是变量
2.长方形的周长为24 cm,其中一边为x(其中x>0),面积为ycm2,则y与x的关系可以写为 ( C )
A.y=x2 B.y=(12-x)2 C.y=(12-x)·x D.y=2(12-x)
3.下表是一项试验的统计数据,表示皮球从高处d落下时,弹跳高度b的情况:下面的式子中能正确表示这种关系的是 ( C ) A.b=d2 B.b=2d C.b= D.b=d+25
4.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( B )
5.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y( cm)与所经过时间x(h)之间的函数关系是 ( C )
6.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,且v17.下面是用棋子摆成的“上”字:
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第④、第⑤个“上”字分别需用_______和_______枚棋子;
(2)第n个“上”字需用_______枚棋子.
【答案】(1)18 22 (2)4n+2
18.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积是_______.
【答案】.10
9.某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数x与甲公司的收费y1(元)的函数关系式;
(2)请写出制作纪念册的册数x与乙公司的收费y2(元)的函数关系式.
【答案】.(1)y1=5x+1500 (2)y2=8x
《课后强化提优》
1.甲、乙两地相距s km,某人行完全程所用的时间t(h)与他的速度v(km/h)满足s=vt,在这个变化过程中,下列判断中错误的是 ( A )
A.s是变量 B.t是变量 C.v是变量 D.s是常量
2.在圆周长公式C=2πr中,变量是 ( C )
A.C、2、π、r B.C、π、r C.C、r D. r
3.如图,将长为30 cm、宽为10 cm的长方形白纸共x张,按下图所示的方法粘合起来,粘合部分的宽度为2 cm,粘合后的总长度为y cm,则y关于x的函数关系式是 ( D )
A.y=30x B.y=28x C.y=28x-2 D.y=28x+2
4.函数的自变量x的取值范围是 ( D )
A.x≠1 B.x>-1
C.x≥-1 D.x≥-1且x≠1
5.小王于上午8时从甲地出发去相距50 km的乙地.右图中,
折线OABC是表示小王离开甲地的时间t(h)与路程s(km)之间
的函数关系的图象,根据图象给出的信息,下列判断中,错
误的是 ( D )
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8:00~9:30相比,小王在10:00~11:00前进的速度较慢
D.出发后1小时,小王走的路程少于25千米
6.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 ( C )
A.第一象限 B.第一、三象限
C.第二、四象限 D.第一、四象限
7.某游客为爬上3 km高的山顶看日出,先用1 h爬了2 km,休息0.5 h后,用1小时爬上山顶.游客爬山所用时间t(h)与山高h(km)间的函数关系用图形表示是 ( D )
8.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( A )
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( D )
10.一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( C )
A.摩托车比汽车晚到1 h
B.A、B两地的路程为20 km
C.摩托车的速度为45 km/h
D.汽车的速度为60 km/h
11.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是_______,自变量x的取值范围是_______
【答案】y=180-2x
12.到邮局投寄平信,每封信的质量不超过20 g时付邮费0. 80元,超过20 g而不超过40 g时付邮费1.60元……依此类推,每增加20 g需增加邮费0.80元(信的质量在100 g内).如果某人投寄一封信的质量为78.5 g,则他应付邮费_______元.
【答案】3.20
13.打字收费标准是每千字5元,打字费m(元)与字数a(个)的函数关系式为_______,自变量a的取值范围是_______.
【答案】m= a≥0
14.某种储蓄的年利率为3.25%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为_______;4年后的本息和为_______元.
【答案】y=32.5x+1000 1130
15如右图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象,根据图象提供的信息,可知该公路的长度是________米.
【答案】504【解析】前两天修了180米,紧接着两天修了(288-180)=108(米),则该公路的长度是:180+108×3=504(米).
16.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明往返的平均速度为________km/h.
【答案】 4 【解析】(6+6)÷3=12÷3=4 (km/h).
17.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离开家的距离与时间的关系可用图中的折线表示.
根据图象回答下列问题:
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时至13时,他们走了多少千米?
返回时,他们的平均速度是多少?
解:(1)他们14时到达离家最远的地方 (2)他们10时开始第一次休息 (3)10时至13时,他们走了5千米 (4)返回时,他们的平均速度是15千米/时,=15(千米/时)
18.某单位计划与某个体车主或某国营出租车公司中的一家签定月租车合同.设汽车每月行驶x千米,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元.在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
(1)当每月行驶的路程不足1 500千米时,租哪家车合算?
(2)当每月行驶的路程为多少时,租两家车的费用相同?
(3)如果估计每月行驶的路程为2 300千米,租用哪家的车合算?
解:观察图象可得:
(1)当每月行驶的路程不足1 500千米时,租出租车公司的车合算;
(2)当每月行驶的路程为1 500千米时,租两家车的费用相同;
(3)如果估计每月行驶的路程为2 300千米,租用个体车主的车合算.
19.小亮步行从家去书店,用一段时间选择自己需要的书籍,然后回家.小亮和家的距离与他离开家以后的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)小亮用多少时间走到书店?小亮家距书店多远?
(2)小亮在书店停留了多长时间?回家用了多少时间?
(3)小亮去书店和回家的步行速度各是多少?
(4)小亮从家里走出10分钟时离家多远?走出50分钟时离家多远?
解:从图中可以看出:
(1)由点A(20,900)可知,小亮去书店用了20分钟,小亮家距书店900米;
(2)由A、B、C三点的横坐标分别是20、40、55可知,他在书店停留的时间为40-20=20(分),小亮回家用了55-40=15(分);
(3)小亮去书店的步行速度为=45(米/分),回家的速度为=60(米/分);
(4)在图象上找出横坐标为10的点D,它的纵坐标为450,因而小亮从家走出10分钟时离家450米;再找出横坐标为50的点E,它的纵坐标为300米,因而小亮从家走出50分钟时离家300米.
知识点扫描
考点一函数的概念和函数的图象
1.函数的概念
(1)在一个变化过程中,我们称数值___________的量为变量,有些数值_____________的,称它们为常量.
(2)一般地,在一个变化过程中,如果有两个变量x与y,并且对于x在其取值范围内的每一个确定的值,y都有_________的值与其对应,那么就说,x是_______,y是x的函数.
(3)用来表示函数关系的数学式子,叫做函数解析式或函数关系式.
2.函数的表示法及自变量的取值范围
(1)函数有三种表示方法:_________,_________,_______,这三种方法有时可以互相转化.
(2)当函数解析式表示实际问题或几何问题时,其自变量的取值范围必须符合实际意义或几何意义.
3.函数的图象:对于一个函数,把自变量x和函数y的每对对应值分别作为点的_______,
_________在平面内描出相应的点,组成这些点的图形叫这个函数的图象.
(1)画函数图象,一般按下列步骤进行:列表、描点、连线.
(2)图象上任一点的坐标是解析式方程的一个解;反之以解析式方程的任意一个解为坐标的点一定在函数图象上.
求函数自变量的取值范围时,首先要考虑自变量的取值必须使解析式有意义.
1.自变量以整式形式出现,它的取值范围是全体实数.
2.自变量以分式形式出现,它的取值范围是使分母不为零的实数.
3.当自变量以偶次方根形式出现,它的取值范围是使被开方数为非负数;以奇次方根出现时,它的取值范围为全体实数.
4.当自变量出现在零次幂或负整数幂的底数中,它的取值范围是使底数不为零的数.
5.在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
经典例题
例1.(1)函数y=的自变量x的取值范围是________.
(2)在函数y=中,自变量x的取值范围是________.
(3)函数y=的自变量x的取值范围是________.
(4)函数y=中自变量x的取值范围是________.
(1)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象.若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
(2)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
(3)甲、乙两人准备在一段长为1 200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s.起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是( )
星期天,小明与小刚骑自行车去距家50千米的某地旅游,匀速行驶1.5小时的时候,其中一辆自行车出故障,因此二人在自行车修理点修车,用了半个小时,然后以原速继续前行,行驶1小时到达目的地.请在右面的平面直角坐标系
中,画出符合他们行驶的路程s(千米)与行驶时间t(时)之间的函数图象.
《当堂过关检测》
1.以固定的速度v0( m/s)向上抛一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t、h是变量 B.v0是常量,t、h是变量
C.v0、-4.9是常量,t、h是变量 D.4.9是常量,v0、t、h是变量
2.长方形的周长为24 cm,其中一边为x(其中x>0),面积为ycm2,则y与x的关系可以写为 ( )
A.y=x2 B.y=(12-x)2 C.y=(12-x)·x D.y=2(12-x)
3.下表是一项试验的统计数据,表示皮球从高处d落下时,弹跳高度b的情况:下面的式子中能正确表示这种关系的是 ( ) A.b=d2 B.b=2d C.b= D.b=d+25
4.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( )
5.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y( cm)与所经过时间x(h)之间的函数关系是 ( )
6.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,且v1
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第④、第⑤个“上”字分别需用_______和_______枚棋子;
(2)第n个“上”字需用_______枚棋子.
8.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积是_______.
9.某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数x与甲公司的收费y1(元)的函数关系式;
(2)请写出制作纪念册的册数x与乙公司的收费y2(元)的函数关系式.
《课后强化提优》
1.甲、乙两地相距s km,某人行完全程所用的时间t(h)与他的速度v(km/h)满足s=vt,在这个变化过程中,下列判断中错误的是 ( )
A.s是变量 B.t是变量 C.v是变量 D.s是常量
2.在圆周长公式C=2πr中,变量是 ( )
A.C、2、π、r B.C、π、r C.C、r D. r
3.如图,将长为30 cm、宽为10 cm的长方形白纸共x张,按下图所示的方法粘合起来,粘合部分的宽度为2 cm,粘合后的总长度为y cm,则y关于x的函数关系式是 ( )
A.y=30x B.y=28x C.y=28x-2 D.y=28x+2
4.函数的自变量x的取值范围是 ( )
A.x≠1 B.x>-1
C.x≥-1 D.x≥-1且x≠1
5.小王于上午8时从甲地出发去相距50 km的乙地.右图中,
折线OABC是表示小王离开甲地的时间t(h)与路程s(km)之间
的函数关系的图象,根据图象给出的信息,下列判断中,错
误的是 ( )
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8:00~9:30相比,小王在10:00~11:00前进的速度较慢
D.出发后1小时,小王走的路程少于25千米
6.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 ( )
A.第一象限 B.第一、三象限
C.第二、四象限 D.第一、四象限
7.某游客为爬上3 km高的山顶看日出,先用1 h爬了2 km,休息0.5 h后,用1小时爬上山顶.游客爬山所用时间t(h)与山高h(km)间的函数关系用图形表示是 ( )
8.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
10.一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( )
A.摩托车比汽车晚到1 h
B.A、B两地的路程为20 km
C.摩托车的速度为45 km/h
D.汽车的速度为60 km/h
11.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是_______,自变量x的取值范围是_______
12.到邮局投寄平信,每封信的质量不超过20 g时付邮费0. 80元,超过20 g而不超过40 g时付邮费1.60元……依此类推,每增加20 g需增加邮费0.80元(信的质量在100 g内).如果某人投寄一封信的质量为78.5 g,则他应付邮费_______元.
13.打字收费标准是每千字5元,打字费m(元)与字数a(个)的函数关系式为_______,自变量a的取值范围是_______.
某种储蓄的年利率为3.25%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为_______;4年后的本息和为_______元.
15如右图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象,根据图象提供的信息,可知该公路的长度是________米.
16.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明往返的平均速度为________km/h.
17.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离开家的距离与时间的关系可用图中的折线表示.
根据图象回答下列问题:
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时至13时,他们走了多少千米?
返回时,他们的平均速度是多少?
18.某单位计划与某个体车主或某国营出租车公司中的一家签定月租车合同.设汽车每月行驶x千米,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元.在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
(1)当每月行驶的路程不足1 500千米时,租哪家车合算?
(2)当每月行驶的路程为多少时,租两家车的费用相同?
(3)如果估计每月行驶的路程为2 300千米,租用哪家的车合算?
19.小亮步行从家去书店,用一段时间选择自己需要的书籍,然后回家.小亮和家的距离与他离开家以后的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)小亮用多少时间走到书店?小亮家距书店多远?
(2)小亮在书店停留了多长时间?回家用了多少时间?
(3)小亮去书店和回家的步行速度各是多少?
(4)小亮从家里走出10分钟时离家多远?走出50分钟时离家多远?
教师样卷
知识点扫描
考点一函数的概念和函数的图象
1.函数的概念
(1)在一个变化过程中,我们称数值发生变化的量为变量,有些数值是始终不变的,称它们为常量.
(2)一般地,在一个变化过程中,如果有两个变量x与y,并且对于x在其取值范围内的每一个确定的值,y都有唯一确定的值与其对应,那么就说,x是自变量,y是x的函数.
(3)用来表示函数关系的数学式子,叫做函数解析式或函数关系式.
2.函数的表示法及自变量的取值范围
(1)函数有三种表示方法:解析法,列表法,图象法,这三种方法有时可以互相转化.
(2)当函数解析式表示实际问题或几何问题时,其自变量的取值范围必须符合实际意义或几何意义.
3.函数的图象:对于一个函数,把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标在平面内描出相应的点,组成这些点的图形叫这个函数的图象.
(1)画函数图象,一般按下列步骤进行:列表、描点、连线.
(2)图象上任一点的坐标是解析式方程的一个解;反之以解析式方程的任意一个解为坐标的点一定在函数图象上.
求函数自变量的取值范围时,首先要考虑自变量的取值必须使解析式有意义.
1.自变量以整式形式出现,它的取值范围是全体实数.
2.自变量以分式形式出现,它的取值范围是使分母不为零的实数.
3.当自变量以偶次方根形式出现,它的取值范围是使被开方数为非负数;以奇次方根出现时,它的取值范围为全体实数.
4.当自变量出现在零次幂或负整数幂的底数中,它的取值范围是使底数不为零的数.
5.在一个函数关系式中,同时有几种代数式,函数自变量的取值范围应是各种代数式中自变量取值范围的公共部分.
经典例题
例1.(1)函数y=的自变量x的取值范围是________.
(2)在函数y=中,自变量x的取值范围是________.
(3)函数y=的自变量x的取值范围是________.
(4)函数y=中自变量x的取值范围是________.
【解答】(1)由x-2≠0得x≠2.
(2)由x+4≥0,得x≥-4.
(3)由得x≥3.
(4)由x+1>0,得x>-1.
(1)如图,是张老师出门散步时离家的距离y与时间x之间的函数关系的图象.若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
(2)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
(3)甲、乙两人准备在一段长为1 200 m的笔直公路上进行跑步,甲、乙跑步的速度分别为4 m/s和6 m/s.起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是( )
【解答】(1)由已知图可知,张老师出门散步可分为3个过程,首先离家越来越远,其次保持一段时间距离不变,最后返回家中,故选D.
(2)从甲地顺流航行到乙地,速度快;逆流航行时速度慢,故顺流航行的图象与x轴的夹角比逆流航行时与x轴的夹角大,图象大致是陡、平、缓,故选C.
(3)乙追上甲所用时间为100÷(6-4)=50(s),乙到达终点所用时间为1 200÷6=200(s),故选C.
星期天,小明与小刚骑自行车去距家50千米的某地旅游,匀速行驶1.5小时的时候,其中一辆自行车出故障,因此二人在自行车修理点修车,用了半个小时,然后以原速继续前行,行驶1小时到达目的地.请在右面的平面直角坐标系
中,画出符合他们行驶的路程s(千米)与行驶时间t(时)之间的函数图象.
【解答】
【点拨】由题意知,速度为50÷(1.5+1)=20(千米/时),20×1.5=30(千米),其中1.5小时~2.0小时s不变.
《当堂过关检测》
1.以固定的速度v0( m/s)向上抛一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( C)
A.4.9是常量,t、h是变量 B.v0是常量,t、h是变量
C.v0、-4.9是常量,t、h是变量 D.4.9是常量,v0、t、h是变量
2.长方形的周长为24 cm,其中一边为x(其中x>0),面积为ycm2,则y与x的关系可以写为 ( C )
A.y=x2 B.y=(12-x)2 C.y=(12-x)·x D.y=2(12-x)
3.下表是一项试验的统计数据,表示皮球从高处d落下时,弹跳高度b的情况:下面的式子中能正确表示这种关系的是 ( C ) A.b=d2 B.b=2d C.b= D.b=d+25
4.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是 ( B )
5.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y( cm)与所经过时间x(h)之间的函数关系是 ( C )
6.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,且v1
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第④、第⑤个“上”字分别需用_______和_______枚棋子;
(2)第n个“上”字需用_______枚棋子.
【答案】(1)18 22 (2)4n+2
18.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,那么△ABC的面积是_______.
【答案】.10
9.某校准备在甲、乙两家公司为毕业班学生制作一批纪念册.甲公司提出:每册收材料费5元,另收设计费1 500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出制作纪念册的册数x与甲公司的收费y1(元)的函数关系式;
(2)请写出制作纪念册的册数x与乙公司的收费y2(元)的函数关系式.
【答案】.(1)y1=5x+1500 (2)y2=8x
《课后强化提优》
1.甲、乙两地相距s km,某人行完全程所用的时间t(h)与他的速度v(km/h)满足s=vt,在这个变化过程中,下列判断中错误的是 ( A )
A.s是变量 B.t是变量 C.v是变量 D.s是常量
2.在圆周长公式C=2πr中,变量是 ( C )
A.C、2、π、r B.C、π、r C.C、r D. r
3.如图,将长为30 cm、宽为10 cm的长方形白纸共x张,按下图所示的方法粘合起来,粘合部分的宽度为2 cm,粘合后的总长度为y cm,则y关于x的函数关系式是 ( D )
A.y=30x B.y=28x C.y=28x-2 D.y=28x+2
4.函数的自变量x的取值范围是 ( D )
A.x≠1 B.x>-1
C.x≥-1 D.x≥-1且x≠1
5.小王于上午8时从甲地出发去相距50 km的乙地.右图中,
折线OABC是表示小王离开甲地的时间t(h)与路程s(km)之间
的函数关系的图象,根据图象给出的信息,下列判断中,错
误的是 ( D )
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8:00~9:30相比,小王在10:00~11:00前进的速度较慢
D.出发后1小时,小王走的路程少于25千米
6.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 ( C )
A.第一象限 B.第一、三象限
C.第二、四象限 D.第一、四象限
7.某游客为爬上3 km高的山顶看日出,先用1 h爬了2 km,休息0.5 h后,用1小时爬上山顶.游客爬山所用时间t(h)与山高h(km)间的函数关系用图形表示是 ( D )
8.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( A )
9.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( D )
10.一辆汽车和一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( C )
A.摩托车比汽车晚到1 h
B.A、B两地的路程为20 km
C.摩托车的速度为45 km/h
D.汽车的速度为60 km/h
11.等腰三角形中顶角的度数y与底角的度数x之间的函数关系式是_______,自变量x的取值范围是_______
【答案】y=180-2x
12.到邮局投寄平信,每封信的质量不超过20 g时付邮费0. 80元,超过20 g而不超过40 g时付邮费1.60元……依此类推,每增加20 g需增加邮费0.80元(信的质量在100 g内).如果某人投寄一封信的质量为78.5 g,则他应付邮费_______元.
【答案】3.20
13.打字收费标准是每千字5元,打字费m(元)与字数a(个)的函数关系式为_______,自变量a的取值范围是_______.
【答案】m= a≥0
14.某种储蓄的年利率为3.25%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为_______;4年后的本息和为_______元.
【答案】y=32.5x+1000 1130
15如右图是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象,根据图象提供的信息,可知该公路的长度是________米.
【答案】504【解析】前两天修了180米,紧接着两天修了(288-180)=108(米),则该公路的长度是:180+108×3=504(米).
16.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明往返的平均速度为________km/h.
【答案】 4 【解析】(6+6)÷3=12÷3=4 (km/h).
17.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离开家的距离与时间的关系可用图中的折线表示.
根据图象回答下列问题:
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时至13时,他们走了多少千米?
返回时,他们的平均速度是多少?
解:(1)他们14时到达离家最远的地方 (2)他们10时开始第一次休息 (3)10时至13时,他们走了5千米 (4)返回时,他们的平均速度是15千米/时,=15(千米/时)
18.某单位计划与某个体车主或某国营出租车公司中的一家签定月租车合同.设汽车每月行驶x千米,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元.在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
(1)当每月行驶的路程不足1 500千米时,租哪家车合算?
(2)当每月行驶的路程为多少时,租两家车的费用相同?
(3)如果估计每月行驶的路程为2 300千米,租用哪家的车合算?
解:观察图象可得:
(1)当每月行驶的路程不足1 500千米时,租出租车公司的车合算;
(2)当每月行驶的路程为1 500千米时,租两家车的费用相同;
(3)如果估计每月行驶的路程为2 300千米,租用个体车主的车合算.
19.小亮步行从家去书店,用一段时间选择自己需要的书籍,然后回家.小亮和家的距离与他离开家以后的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)小亮用多少时间走到书店?小亮家距书店多远?
(2)小亮在书店停留了多长时间?回家用了多少时间?
(3)小亮去书店和回家的步行速度各是多少?
(4)小亮从家里走出10分钟时离家多远?走出50分钟时离家多远?
解:从图中可以看出:
(1)由点A(20,900)可知,小亮去书店用了20分钟,小亮家距书店900米;
(2)由A、B、C三点的横坐标分别是20、40、55可知,他在书店停留的时间为40-20=20(分),小亮回家用了55-40=15(分);
(3)小亮去书店的步行速度为=45(米/分),回家的速度为=60(米/分);
(4)在图象上找出横坐标为10的点D,它的纵坐标为450,因而小亮从家走出10分钟时离家450米;再找出横坐标为50的点E,它的纵坐标为300米,因而小亮从家走出50分钟时离家300米.
同课章节目录
