2.1数列课件1(苏教版必修5)
图片预览








文档简介
(共29张PPT)
数 列
2008----北京奥运,从1984年到2004年,我国共参加了6次奥运会,各次参赛获得的金牌总数写成一列:
15 ,
5 ,
16 ,
28 ,
32.
一、新课引入
1、奥运会金牌数
1,
2,
3,
4,
… ,
49.
我们班每位同学都有一学号,把本班学生的学号由小到大排列成一列数:
2、学生学号
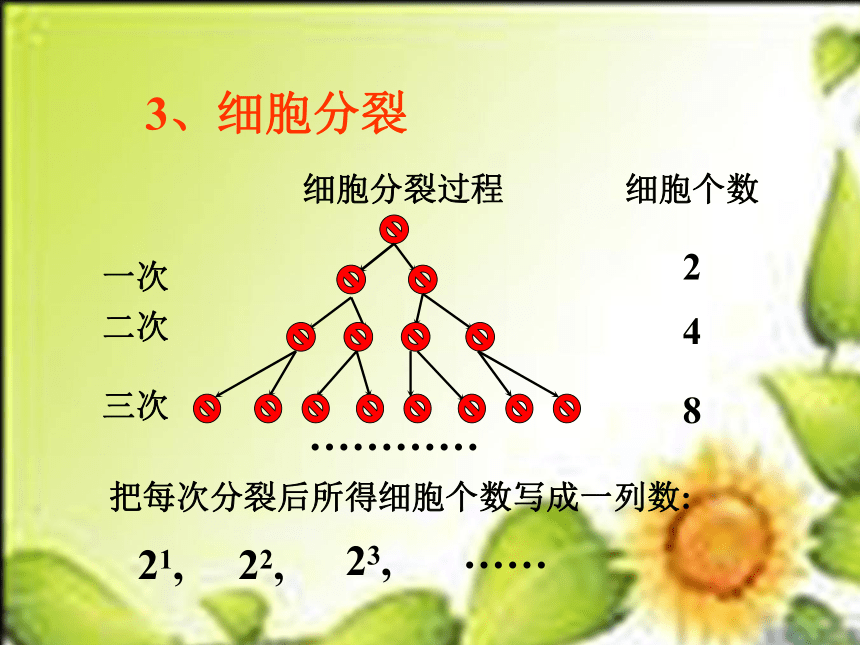
3、细胞分裂
细胞分裂过程
细胞个数
一次
2
二次
4
三次
8
…………
把每次分裂后所得细胞个数写成一列数:
21,
22,
23,
……
都是按照一定次序排列的数。
1/2, 1/3, 1/4,… . ④
1,1, 1,1,…. ⑤
15,5,16,28,32 ①
1,2,3,4,… , 49 ②
21, 22, 23, …. ③
五组数据共同点是什么?
1、什么叫数列?数列与数集有何区别和联系?
2、什么是数列的项、首项?按项数的多少可把数列怎样分类?
3、数列一般形式是什么?{an}与 an 相同吗?
4、数列的通项公式是如何定义的?你能全部写出上述数列的通项公式吗?通项公式惟一吗?
5、你是怎样理解函数与数列的联系的?你能否画出上述数列的图象?
二、阅读理解
三、交流合作
在阅读理解的基础上,请以前后两桌的4位同学为一组,展开交流讨论,逐一解决上述问题。
定义:按一定次序排列的一列数叫数列
(3)数列中的数是有顺序的,而数集合的数是无序的。
(2)数列中的数是可重复的,而数集中的数是互异的。
(1)数列与数集都是具有某种共同属性的数的全体。
1、什么是数列?数列与数集有何区别和联系?
四、成果展示
返回
(2)分类:项数有限的数列叫有穷数列;
项数无限的数列叫做无穷数列。
(1)项:数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(或首相),第2项,······,第n项, ······
返回
2、什么是数列的项、首项?
按项数的多少可把数列怎样分类?
数列的一般形式可以写成:
a1,a2,…,an,… 简记为{an}。
{an}是一个数列,而an是数列的第n项。
思考:
21, 22, 23, … . ③
上述数列的第n项是什么?
3、数列一般形式是什么?{an}与 an 相同吗?
项 : 21 22 23 24 …
你是如何得出数列{2n}中的第n项an与它的位置序号n之的关系的?
↓
数列③:
∴ an =2n (n ∈ N*)
↓
↓
↓
↓
n
2n
…
…
返回
序号: 1 2 3 4 …
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
4.1数列的通项公式是如何定义的?
4.2你能全部写出下列数列的通项公式吗?
1/2,1/3,1/4,… ④
1, 1, 1, 1, … ⑤
15,5,16,28,32 ①
1,2,3,4,… , 50 ②
21, 22, 23, … . ③
15,5,16,28,32
数列①
写不出通项公式。
哎,an与n之的关系无法用公式表示。
数列②
1 2 3 … 49
项
序号
1 2 3 … 49
↓
↓
↓
↓
an= n
(1≤n≤49且n∈N*)
此数列为有穷数列,要注意n的范围哦!
数列④
↓ ↓ ↓ ↓
项
1 2 3 4 ……
序号
↓ ↓ ↓ ↓
不要写成an=1/n 哦!
数列⑤ :
序号: 1 2 3 4 …
项: -1 1 -1 1 …
(-1)1 (-1)2 (-1)3 (-1)4…
或 an=(-1)n (n∈N*)
{
-1 (n为奇数)
1 (n为偶数)
∴ an=
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
哇!有两个唉
结论:1.并不是所有的数列都有通项公式。
如数列①
2.数列的通项公式不是唯一确定的。
如数列⑤
返回
4.3数列是否一定有通项公式?
数列通项公式惟一吗?
5.1你是怎样理解函数与数列的联系的?
数列实质: 从函数的观点看,数列可以看作是自变量取值集合是正整数集 N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,通项公式即相应的函数解析式。
x
y
n
an
自变量
函数值
15,5,16,28,32 ①
1,2,3,4,… , 49 ②
21, 22, 23, …. ③
1/2,1/3,1/4,… . ④
1,1, 1,1,…. ⑤
5.2你能否画出下面数列的图象?
0 1 2 3 4 5 6 n
2
4
8
16
an
数列图象是一些点
0 1 2 3 4 5 6 7 n
an
1
这些点是 孤立的!
1、根据下面数列{an}的通项公式,
写出它的前5项
(2)1, - 4,7, - 10,13
和第n+1项:
五、巩固性练习
2、观察下面数列的特点,用适当的数填空,并写出该数列的一个通项公式。
(1) ( ) , 2, 4 , 8 , ( ) , 32.
16
1
(2)1,4,9,16,( ) ,36,( ).
49
25
在庆祝第20个教师节活动中,学校为烘托节日气氛,在200米长的校园主干道一侧,从起点开始,每隔3米插一面彩旗,由近及远排成一列,迎风飘扬。问最后一面旗子会插在终点处吗?一共应插多少面旗子?
六、发展性练习
0
3
6
9
200
……
若从距离起点2米开始,每隔3米插一面彩旗,则在距离起点80米处是否应该插旗?若是,是第几面旗子?
2
5
8
11
80
…
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
n
↓
↓
答:应该插第27面旗子
七、小结回顾
本节课主要学习了以下内容:
1.数列的定义及其分类;
3.数列的通项公式:
①会由通项公式 求数列的特定项;
②会由数列的前几项写出数列通项公式。
2.数列与函数的关系及其图象。
数 列
2008----北京奥运,从1984年到2004年,我国共参加了6次奥运会,各次参赛获得的金牌总数写成一列:
15 ,
5 ,
16 ,
28 ,
32.
一、新课引入
1、奥运会金牌数
1,
2,
3,
4,
… ,
49.
我们班每位同学都有一学号,把本班学生的学号由小到大排列成一列数:
2、学生学号
3、细胞分裂
细胞分裂过程
细胞个数
一次
2
二次
4
三次
8
…………
把每次分裂后所得细胞个数写成一列数:
21,
22,
23,
……
都是按照一定次序排列的数。
1/2, 1/3, 1/4,… . ④
1,1, 1,1,…. ⑤
15,5,16,28,32 ①
1,2,3,4,… , 49 ②
21, 22, 23, …. ③
五组数据共同点是什么?
1、什么叫数列?数列与数集有何区别和联系?
2、什么是数列的项、首项?按项数的多少可把数列怎样分类?
3、数列一般形式是什么?{an}与 an 相同吗?
4、数列的通项公式是如何定义的?你能全部写出上述数列的通项公式吗?通项公式惟一吗?
5、你是怎样理解函数与数列的联系的?你能否画出上述数列的图象?
二、阅读理解
三、交流合作
在阅读理解的基础上,请以前后两桌的4位同学为一组,展开交流讨论,逐一解决上述问题。
定义:按一定次序排列的一列数叫数列
(3)数列中的数是有顺序的,而数集合的数是无序的。
(2)数列中的数是可重复的,而数集中的数是互异的。
(1)数列与数集都是具有某种共同属性的数的全体。
1、什么是数列?数列与数集有何区别和联系?
四、成果展示
返回
(2)分类:项数有限的数列叫有穷数列;
项数无限的数列叫做无穷数列。
(1)项:数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(或首相),第2项,······,第n项, ······
返回
2、什么是数列的项、首项?
按项数的多少可把数列怎样分类?
数列的一般形式可以写成:
a1,a2,…,an,… 简记为{an}。
{an}是一个数列,而an是数列的第n项。
思考:
21, 22, 23, … . ③
上述数列的第n项是什么?
3、数列一般形式是什么?{an}与 an 相同吗?
项 : 21 22 23 24 …
你是如何得出数列{2n}中的第n项an与它的位置序号n之的关系的?
↓
数列③:
∴ an =2n (n ∈ N*)
↓
↓
↓
↓
n
2n
…
…
返回
序号: 1 2 3 4 …
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
4.1数列的通项公式是如何定义的?
4.2你能全部写出下列数列的通项公式吗?
1/2,1/3,1/4,… ④
1, 1, 1, 1, … ⑤
15,5,16,28,32 ①
1,2,3,4,… , 50 ②
21, 22, 23, … . ③
15,5,16,28,32
数列①
写不出通项公式。
哎,an与n之的关系无法用公式表示。
数列②
1 2 3 … 49
项
序号
1 2 3 … 49
↓
↓
↓
↓
an= n
(1≤n≤49且n∈N*)
此数列为有穷数列,要注意n的范围哦!
数列④
↓ ↓ ↓ ↓
项
1 2 3 4 ……
序号
↓ ↓ ↓ ↓
不要写成an=1/n 哦!
数列⑤ :
序号: 1 2 3 4 …
项: -1 1 -1 1 …
(-1)1 (-1)2 (-1)3 (-1)4…
或 an=(-1)n (n∈N*)
{
-1 (n为奇数)
1 (n为偶数)
∴ an=
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
哇!有两个唉
结论:1.并不是所有的数列都有通项公式。
如数列①
2.数列的通项公式不是唯一确定的。
如数列⑤
返回
4.3数列是否一定有通项公式?
数列通项公式惟一吗?
5.1你是怎样理解函数与数列的联系的?
数列实质: 从函数的观点看,数列可以看作是自变量取值集合是正整数集 N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,通项公式即相应的函数解析式。
x
y
n
an
自变量
函数值
15,5,16,28,32 ①
1,2,3,4,… , 49 ②
21, 22, 23, …. ③
1/2,1/3,1/4,… . ④
1,1, 1,1,…. ⑤
5.2你能否画出下面数列的图象?
0 1 2 3 4 5 6 n
2
4
8
16
an
数列图象是一些点
0 1 2 3 4 5 6 7 n
an
1
这些点是 孤立的!
1、根据下面数列{an}的通项公式,
写出它的前5项
(2)1, - 4,7, - 10,13
和第n+1项:
五、巩固性练习
2、观察下面数列的特点,用适当的数填空,并写出该数列的一个通项公式。
(1) ( ) , 2, 4 , 8 , ( ) , 32.
16
1
(2)1,4,9,16,( ) ,36,( ).
49
25
在庆祝第20个教师节活动中,学校为烘托节日气氛,在200米长的校园主干道一侧,从起点开始,每隔3米插一面彩旗,由近及远排成一列,迎风飘扬。问最后一面旗子会插在终点处吗?一共应插多少面旗子?
六、发展性练习
0
3
6
9
200
……
若从距离起点2米开始,每隔3米插一面彩旗,则在距离起点80米处是否应该插旗?若是,是第几面旗子?
2
5
8
11
80
…
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
n
↓
↓
答:应该插第27面旗子
七、小结回顾
本节课主要学习了以下内容:
1.数列的定义及其分类;
3.数列的通项公式:
①会由通项公式 求数列的特定项;
②会由数列的前几项写出数列通项公式。
2.数列与函数的关系及其图象。
