2.1向量的概念及表示课件(苏教版必修4)
文档属性
| 名称 | 2.1向量的概念及表示课件(苏教版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 494.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-24 09:56:36 | ||
图片预览





文档简介
(共20张PPT)
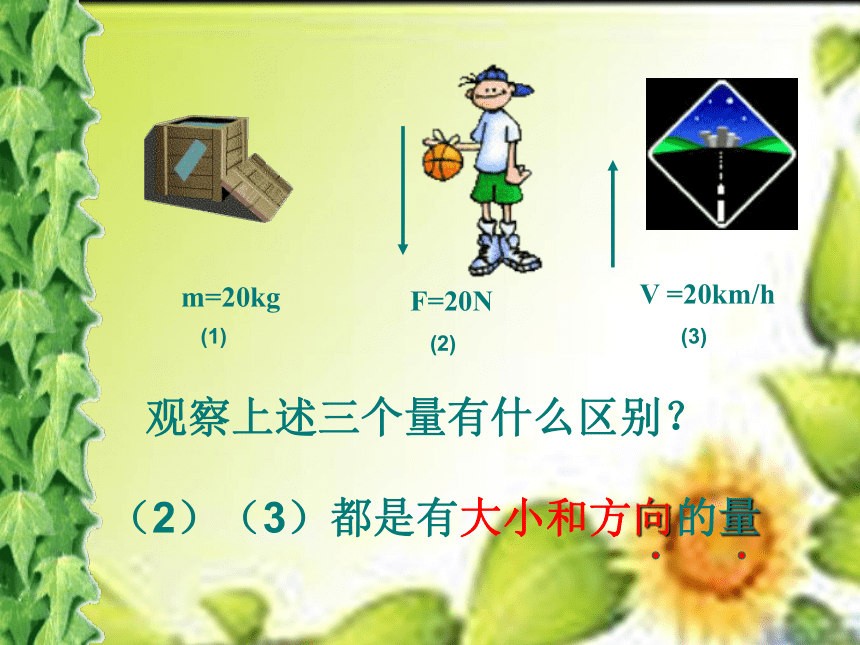
据报道:我国用来发射“神舟六号”宇宙飞船推力约为2万牛,每个航天员的质量约为65kg,火箭进入轨道后的速度约为708km/s。上述力、质量、速度这些在生产生活中常见 的量我们如何用数学模型来刻画呢?这个数学模型又有些什么性质与用途呢?
F=20N
V =20km/h
(2)(3)都是有大小和方向的量
m=20kg
(1)
(2)
(3)
观察上述三个量有什么区别?
向量的概念及表示:
1.向量的定义:
2.向量的表示方法:
3.向量的大小:
记作:
4.两个特殊向量:
零向量:
单位向量:
既有大小又有方向的量称为向量.
(或称为 模 )
指向量的长度
长度为0的向量称为~
长度等于1个单位长度的向量,叫做~
记作:
1)几何表示;
2)代数表示;
向量之间的关系:
5.平行向量的定义:
一组方向相同或相反的非零向量叫做~
我们规定零向量与任一向量平行
两向量的平行与平面几何里两线段的平行有什么区别?
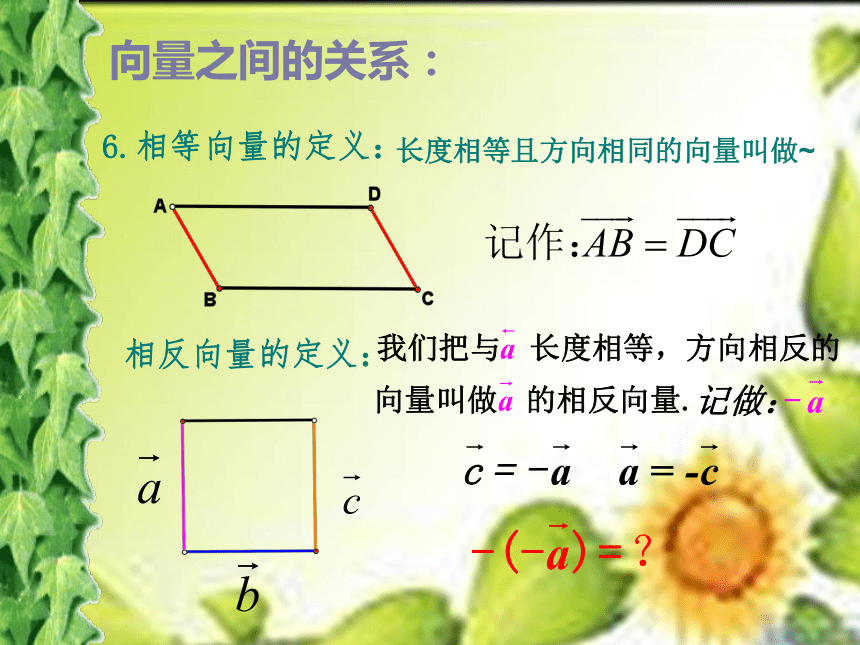
6.相等向量的定义:
长度相等且方向相同的向量叫做~
相反向量的定义:
向量之间的关系:
任意一组平行向量都可以平移到同一直线上
向量之间的关系:
7.共线向量与平行向量的关系:
平行向量就是共线向量
两向量的共线与平面几何里两线段的共线是否一样?
为什么?
例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:
解:
A
B
概念辨析:
×
×
×
×
×
√
×
√
合作探究:
练习:
1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
4.两个特殊向量:
零向量:
单位向量:
5.平行向量的定义:
6.相等向量的定义
相反向量的定义:
7.共线向量与平行向量的关系:
小 结:
课后作业:
研究作业:
谢谢!
谢谢!
(1)
用有向线段表示;
(2)
i)用有向线段的起点与终点字母来表示;
ii)用小写的字母来表示;
A(起点)
B(终点)
上述向量还可表示为:
有向线段的长度表示向量的大小
注意:起点一定要写在终点的前面
几何表示:
代数表示:
箭头所指的方向表示向量的方向
两个特殊向量:
2、单位向量:长度为 1 个单位长度的向量。
零向量大小为0,方向不确定的.可以是任意方向.
1
单位向量大小为1,方向不一定相同。
所以零向量只有一个,而单位向量可以有无数个
1、零向量:长度为 0 的向量。记作 0
思考:平面直角坐标系内,起点在原点的单位向量,
它们的终点的轨迹是什么图形?
有向线段:
规定了方向(即规定了起点和终点)的线段称为~
通常在有向线段的终点处画上箭头表示它的方向.
A(起点)
B(终点)
如图:AB叫有向线段
我们现在所研究的向量,与起点位置无关.
所以数学中的向量也叫 自由向量
用有向线段表示向量时,起点可以取任意位置。
据报道:我国用来发射“神舟六号”宇宙飞船推力约为2万牛,每个航天员的质量约为65kg,火箭进入轨道后的速度约为708km/s。上述力、质量、速度这些在生产生活中常见 的量我们如何用数学模型来刻画呢?这个数学模型又有些什么性质与用途呢?
F=20N
V =20km/h
(2)(3)都是有大小和方向的量
m=20kg
(1)
(2)
(3)
观察上述三个量有什么区别?
向量的概念及表示:
1.向量的定义:
2.向量的表示方法:
3.向量的大小:
记作:
4.两个特殊向量:
零向量:
单位向量:
既有大小又有方向的量称为向量.
(或称为 模 )
指向量的长度
长度为0的向量称为~
长度等于1个单位长度的向量,叫做~
记作:
1)几何表示;
2)代数表示;
向量之间的关系:
5.平行向量的定义:
一组方向相同或相反的非零向量叫做~
我们规定零向量与任一向量平行
两向量的平行与平面几何里两线段的平行有什么区别?
6.相等向量的定义:
长度相等且方向相同的向量叫做~
相反向量的定义:
向量之间的关系:
任意一组平行向量都可以平移到同一直线上
向量之间的关系:
7.共线向量与平行向量的关系:
平行向量就是共线向量
两向量的共线与平面几何里两线段的共线是否一样?
为什么?
例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:
解:
A
B
概念辨析:
×
×
×
×
×
√
×
√
合作探究:
练习:
1.向量的定义:
2.向量的表示方法:
3.向量的大小又称为:
4.两个特殊向量:
零向量:
单位向量:
5.平行向量的定义:
6.相等向量的定义
相反向量的定义:
7.共线向量与平行向量的关系:
小 结:
课后作业:
研究作业:
谢谢!
谢谢!
(1)
用有向线段表示;
(2)
i)用有向线段的起点与终点字母来表示;
ii)用小写的字母来表示;
A(起点)
B(终点)
上述向量还可表示为:
有向线段的长度表示向量的大小
注意:起点一定要写在终点的前面
几何表示:
代数表示:
箭头所指的方向表示向量的方向
两个特殊向量:
2、单位向量:长度为 1 个单位长度的向量。
零向量大小为0,方向不确定的.可以是任意方向.
1
单位向量大小为1,方向不一定相同。
所以零向量只有一个,而单位向量可以有无数个
1、零向量:长度为 0 的向量。记作 0
思考:平面直角坐标系内,起点在原点的单位向量,
它们的终点的轨迹是什么图形?
有向线段:
规定了方向(即规定了起点和终点)的线段称为~
通常在有向线段的终点处画上箭头表示它的方向.
A(起点)
B(终点)
如图:AB叫有向线段
我们现在所研究的向量,与起点位置无关.
所以数学中的向量也叫 自由向量
用有向线段表示向量时,起点可以取任意位置。
