2.2向量的加减法课件(苏教版必修4)
文档属性
| 名称 | 2.2向量的加减法课件(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-24 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
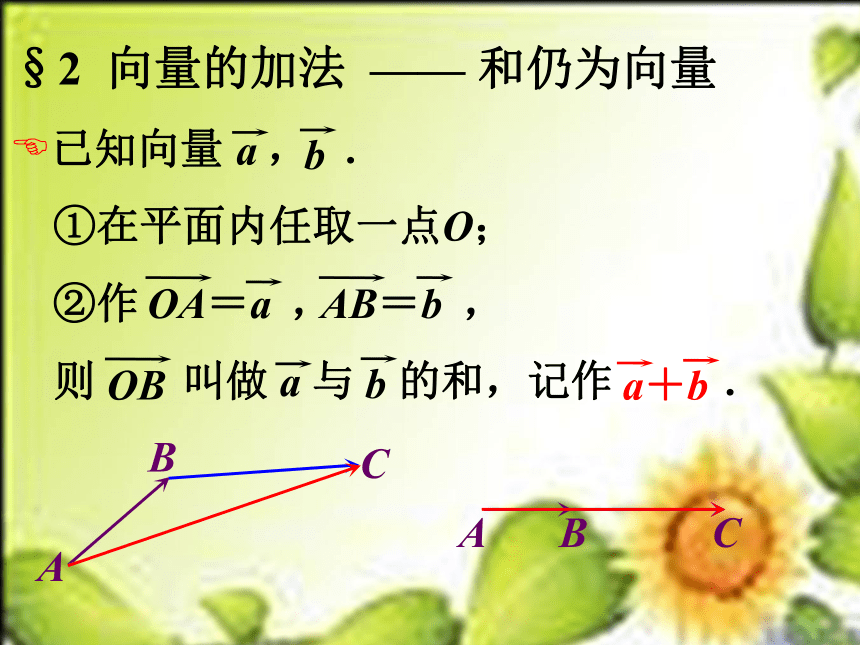
§2 向量的加法 —— 和仍为向量
已知向量 , .
①在平面内任取一点O;
②作 , ,
则 叫做 与 的和,记作 .
B
A
C
A
B
C
a
b
OA=a
AB=b
OB
a
b
a+b
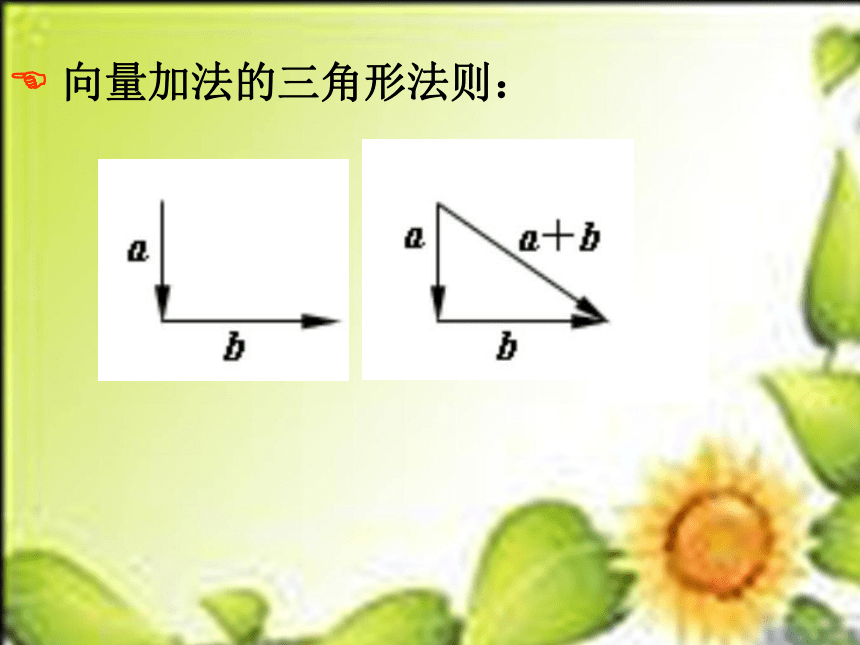
向量加法的三角形法则:
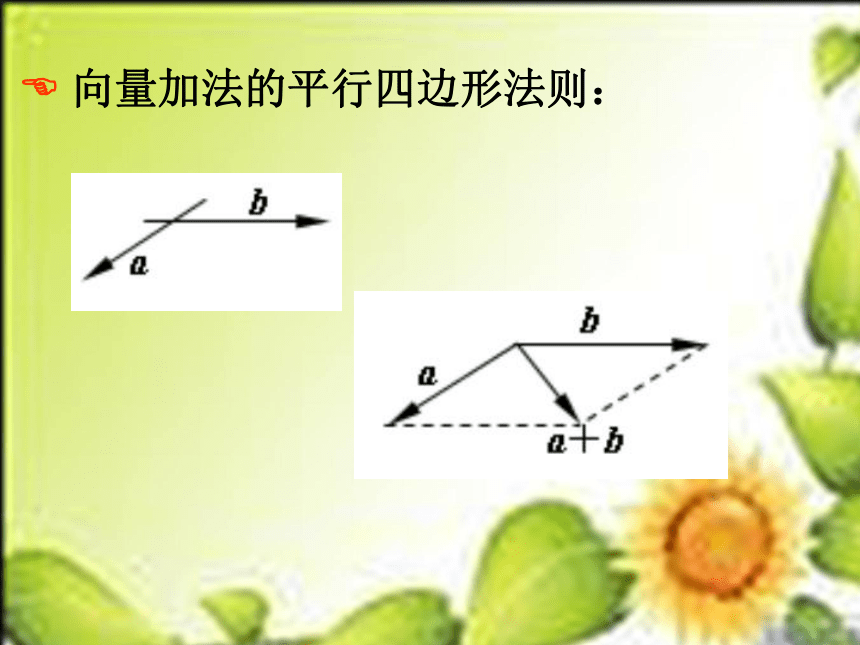
向量加法的平行四边形法则:
,
.
向量的加法满足交换律、结合律:
,
.
a+0=0+a=a
a+(- a )=( -a )+a = 0
a+b=b+a
( a+b )+c = a+( b+c )
练习.
化简下列各式:
① ;
② ;
③ .
例 如图,点O是正六边形ABCDEF的中心,
设BA=a,BC=b.
试用a,b表示向量OE,BF,BD.
§3 向量的减法 —— 差仍为向量
向量的减法是向量加法的逆运算.
若 ,
则 叫做 与 的差,记作 .
作图:①两向量 , 起点相同;
②连接两终点;
③差向量方向指向被减向量.
b+x=a
x
b
a-b
a
a
b
a-b =a+(- b )
练习.
1.若b=AB,c=AC,则BC=( )
A.b-c B.c-b
C.b+c D.-b-c
2.化简:
① AB-AC+BD-CD+AD;
② AB+MB+BO+OM;
③ AB+DA+BD-BC-CA.
B
练习.
3.在正六边形ABCDEF中,
设AB=a,AE=b.
表示下列向量:
DE;AD;BC;EF;
CD;AC;CE;FA.
A
B
C
D
E
F
练习.
4.如图,在□ABCD中,已知OA=a,
OB=b,OC=c.
试用a,b,c表示向量OD.
练习.
5.已知:P、Q为△ABC的边BC上两点,
且BP=QC.
求证:AB+AC=AP+AQ.
§2 向量的加法 —— 和仍为向量
已知向量 , .
①在平面内任取一点O;
②作 , ,
则 叫做 与 的和,记作 .
B
A
C
A
B
C
a
b
OA=a
AB=b
OB
a
b
a+b
向量加法的三角形法则:
向量加法的平行四边形法则:
,
.
向量的加法满足交换律、结合律:
,
.
a+0=0+a=a
a+(- a )=( -a )+a = 0
a+b=b+a
( a+b )+c = a+( b+c )
练习.
化简下列各式:
① ;
② ;
③ .
例 如图,点O是正六边形ABCDEF的中心,
设BA=a,BC=b.
试用a,b表示向量OE,BF,BD.
§3 向量的减法 —— 差仍为向量
向量的减法是向量加法的逆运算.
若 ,
则 叫做 与 的差,记作 .
作图:①两向量 , 起点相同;
②连接两终点;
③差向量方向指向被减向量.
b+x=a
x
b
a-b
a
a
b
a-b =a+(- b )
练习.
1.若b=AB,c=AC,则BC=( )
A.b-c B.c-b
C.b+c D.-b-c
2.化简:
① AB-AC+BD-CD+AD;
② AB+MB+BO+OM;
③ AB+DA+BD-BC-CA.
B
练习.
3.在正六边形ABCDEF中,
设AB=a,AE=b.
表示下列向量:
DE;AD;BC;EF;
CD;AC;CE;FA.
A
B
C
D
E
F
练习.
4.如图,在□ABCD中,已知OA=a,
OB=b,OC=c.
试用a,b,c表示向量OD.
练习.
5.已知:P、Q为△ABC的边BC上两点,
且BP=QC.
求证:AB+AC=AP+AQ.
