2.2等差数列的前n项和课件(苏教版必修5)
文档属性
| 名称 | 2.2等差数列的前n项和课件(苏教版必修5) |  | |
| 格式 | rar | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-24 09:56:36 | ||
图片预览





文档简介
(共16张PPT)
a、b、c成等差数列
2b= a+c
{an}为等差数列
an+1- an=d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
b为a、c 的等差中项
知识回顾
3.更一般的情形,an= ,
d=
am+(n - m) d
4.在等差数列{an}中,由
m+n=p+q
m,n,p,q∈N★
am+an=ap+aq
5. 在等差数列{an}中a1+an a2+ an-1
a3+ an-2 …
=
=
=
10岁的高斯(德国)的算法:
首项与末项的和:1+100=101
第2项与倒数第2项的和:2+99=101
第3项与倒数第3项的和:3+98=101
………………………………………
第50项与倒数第50项的和:50+51=101
∴101×(100/2)=5050
引例:1+2+3+…+100=?
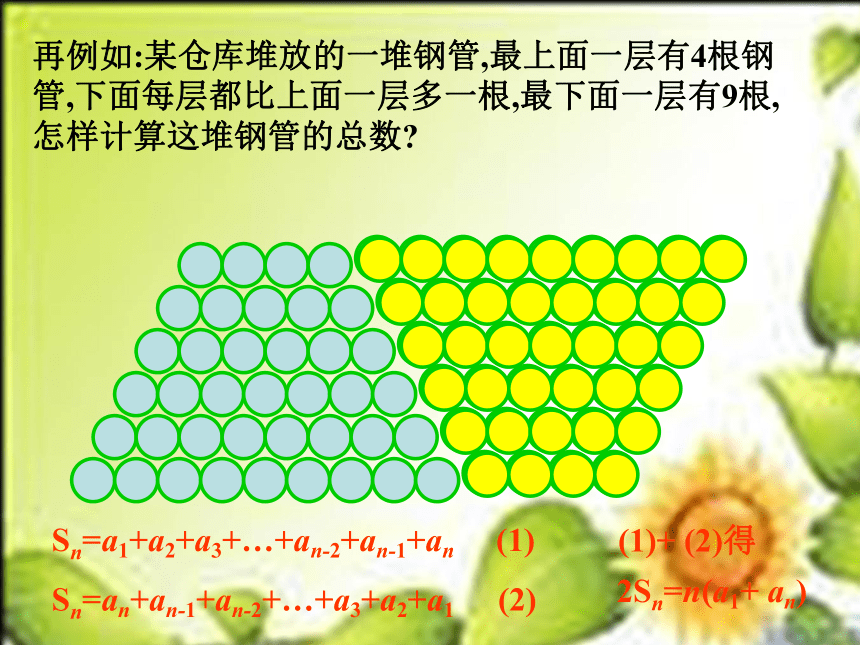
再例如:某仓库堆放的一堆钢管,最上面一层有4根钢管,下面每层都比上面一层多一根,最下面一层有9根,怎样计算这堆钢管的总数
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
(1)+ (2)得
2Sn=n(a1+ an)
新课学习
㈠等差数列前n 项和Sn = = .
=an2+bn
a、b 为常数
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
(1)+ (2)得
2Sn=n(a1+ an)
①推导等差数列的前n项和公式的方法叫 ;
②等差数列的前n项和公式类同于 ;
③{an}为等差数列 ,这是一个关于 的
没有 的“ ”
倒序相加法
梯形的面积公式
Sn=an2+bn
n
常数项
二次函数
( 注意 a 还可以是 0)
例1 已知数列{an}中Sn=2n2+3n,
求证:{an}是等差数列.
三、公式的应用:
根据下列各题中的条件,求相应的等差数列{an}的Sn
(1)a1=5,a50=101,n=50
(2)a1=100,d=-2,n=50
S50=2600
S50=2550
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
三、课堂练习
a1 d n an sn
5 10 10
-2 50 2550
-38 -10 -360
14.5 26 32
95
500
100
2
2
15
0.7
604.5
例3、等差数列 { a n } 中,S 15 = 90,求 a 8
法一:a 1 + a 1 + 14d = 12
即 a 1 + a 15 = 12
即 a 1 + 7d = 6
∴ a 8 = a 1 + 7d = 6
= 6
归纳:选用中项求等差数列的前 n 项之和 S n
当 n 为奇数时,S n = ____________;
当 n 为偶数时, S n = _______________________。
例4、一个等差数列,共有 10 项,其中奇数项的和为 125,
偶数项的和为 15,求 a 1、d。
法二:相减得 5 d = -110
即 d = -22
归纳:等差数列中,
n 为奇数,必有
________________
n 为偶数,必有
________________
课堂练习
课本P:41页
练习:1,2,3,4
a、b、c成等差数列
2b= a+c
{an}为等差数列
an+1- an=d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
b为a、c 的等差中项
知识回顾
3.更一般的情形,an= ,
d=
am+(n - m) d
4.在等差数列{an}中,由
m+n=p+q
m,n,p,q∈N★
am+an=ap+aq
5. 在等差数列{an}中a1+an a2+ an-1
a3+ an-2 …
=
=
=
10岁的高斯(德国)的算法:
首项与末项的和:1+100=101
第2项与倒数第2项的和:2+99=101
第3项与倒数第3项的和:3+98=101
………………………………………
第50项与倒数第50项的和:50+51=101
∴101×(100/2)=5050
引例:1+2+3+…+100=?
再例如:某仓库堆放的一堆钢管,最上面一层有4根钢管,下面每层都比上面一层多一根,最下面一层有9根,怎样计算这堆钢管的总数
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
(1)+ (2)得
2Sn=n(a1+ an)
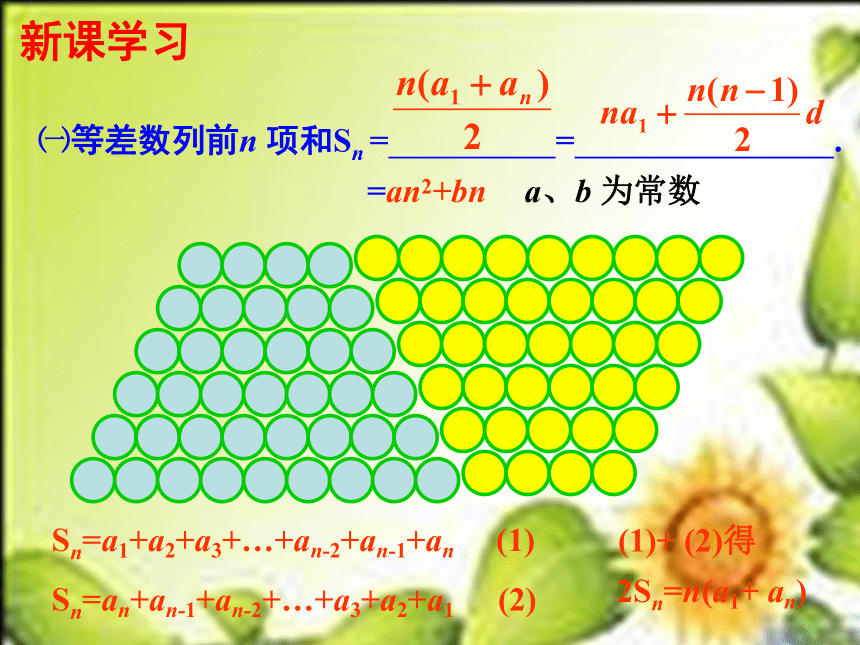
新课学习
㈠等差数列前n 项和Sn = = .
=an2+bn
a、b 为常数
Sn=a1+a2+a3+…+an-2+an-1+an (1)
Sn=an+an-1+an-2+…+a3+a2+a1 (2)
(1)+ (2)得
2Sn=n(a1+ an)
①推导等差数列的前n项和公式的方法叫 ;
②等差数列的前n项和公式类同于 ;
③{an}为等差数列 ,这是一个关于 的
没有 的“ ”
倒序相加法
梯形的面积公式
Sn=an2+bn
n
常数项
二次函数
( 注意 a 还可以是 0)
例1 已知数列{an}中Sn=2n2+3n,
求证:{an}是等差数列.
三、公式的应用:
根据下列各题中的条件,求相应的等差数列{an}的Sn
(1)a1=5,a50=101,n=50
(2)a1=100,d=-2,n=50
S50=2600
S50=2550
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表:
三、课堂练习
a1 d n an sn
5 10 10
-2 50 2550
-38 -10 -360
14.5 26 32
95
500
100
2
2
15
0.7
604.5
例3、等差数列 { a n } 中,S 15 = 90,求 a 8
法一:a 1 + a 1 + 14d = 12
即 a 1 + a 15 = 12
即 a 1 + 7d = 6
∴ a 8 = a 1 + 7d = 6
= 6
归纳:选用中项求等差数列的前 n 项之和 S n
当 n 为奇数时,S n = ____________;
当 n 为偶数时, S n = _______________________。
例4、一个等差数列,共有 10 项,其中奇数项的和为 125,
偶数项的和为 15,求 a 1、d。
法二:相减得 5 d = -110
即 d = -22
归纳:等差数列中,
n 为奇数,必有
________________
n 为偶数,必有
________________
课堂练习
课本P:41页
练习:1,2,3,4
