2.2等差数列课件1(苏教版必修5)
图片预览








文档简介
(共20张PPT)
等 差 数 列
定义:按一定次序排列的一列数叫数列
(3)数列中的数是有顺序的,而数集合的数是无序的。
(2)数列中的数是可重复的,而数集中的数是互异的。
(1)数列与数集都是具有某种共同属性的 数的全体。
知识回顾
数列与数集有何区别和联系
数列
分类:项数有限的数列叫有穷数列;
项:数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(或首相),第2项,······,第n项, ······
数列分类
数列的项、首项
项数无限的数列叫做无穷数列。
数列的一般形式可以写成:
a1,a2,…,an,… 简记为{an}。
{an}是一个数列,而an是数列的第n项。
{an}与 an 的区别
数列一般形式
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
数列的通项公式的定义
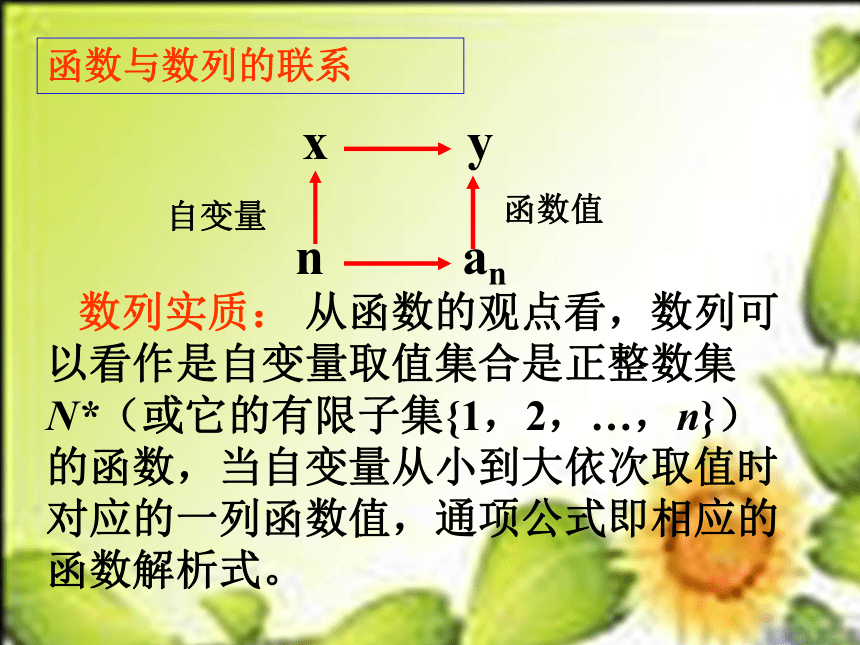
函数与数列的联系
数列实质: 从函数的观点看,数列可以看作是自变量取值集合是正整数集 N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,通项公式即相应的函数解析式。
x
y
n
an
自变量
函数值
课堂练习
已知数列{an}的前四项是:9 ,4, —1,……,
则数列{an}的通项公式an = ,
2. 数列1,1,2,3,5,8,13,x,34,55,…中的x
等于( )
A. 19 B. 20 C. 21 D. 22
an+2= an+1+an
C
3. 已知数列{an}的前四项是:1 ,-3, 5,-7,……,
则-101在不在数列{an}中 ,
不在
14 - 5n
4. 上面几个数列,它们有没有规律
阅读课本33-34页并弄清:
1.什么样的数列是等差数列?
2.什么是等差数列的公差?
3.等差数列相邻两项与公差的关系
4.等差数列连续三项之间的关系
5.等差数列的通项公式是什么
6.等差数列的图象的特征是什么?
③推导等差数列通项公式的方法叫做 法.
递推
每一项与
它前一项的差
学习新课
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
①数列{ an }为等差数列 ;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
由定义归纳通项公式
a2 - a1=d,
a3 - a2=d,
a4 - a3=d,
……
则 a2=a1+d
a3=a2+d=a1+2d
a4=a3+d=a1+3d
……
由此得到 a n=a1+(n-1)d
an-1-an-2=d,
an -an-1=d.
这(n-1)个式子迭加
an - a1= (n-1)d
当n=1时,上式两边均等于a1,即等式也成立的。这表明当n∈N*时上式都成立,因而它就是等差数列{an}的通项公式。
判定下列数列是否可能是等差数列?
1. 9 ,8,7,6,5,4,……;
2. 1,1,1,1,……;
3. 1,0,1,0,1,……;
4. 0,2,3,4,5,……;
5. m, m, m, m, ……;
6. 1,11,21,31,41,…….
√
√
√
√
×
×
课堂练习
2.判断题:
①数列a,2a,3a,4a,…是等差数列( )
②若an-an+1=3 (n∈N*),则{an}是公差为3
的等差数列。 ( )
若a2-a1=a3-a2, 则数列{an}是等差数
列 ( )
1、等差数列要求从第2项起,后一项与
前一项作差。 不能颠倒。
2、作差的结果要求是同一个常数。
可以是整数,也可以是0和负数。
③
对等差数列的定义的理解
1.如果一个数列,不是从第2项起,而是
从第3项起或第4项起,每一项与它前一
项的差是同一个常数,那 么这个数列不
是等差数列.
2.一个数列从第2项起,每一项与它前一
项的差尽管等于常数,这个数列也不一
定是等差数列,因为这些常数不一定相
同.当这些常数不同时,此数列不是等
差数列
对等差数列的定义的理解
3.求公差时,要注意相邻两项相减的顺序
d=an+1-an或d=an-an-1(n≥2)
4. 要判断一个数列是不是等差数列,只要
看对于任意正整数n,an-an-1,是不是通
一个常数,切记不可通过计算a2-a1,a3-a2
等有限的几个式子的值后,发现它一个
常数,就得出该数列为等差数列的结论
等差中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等差数列:
(1)2 , , 4 (2)-1, ,5
(3)-12, ,0 (4)0, ,0
3
2
-6
0
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
求出下列等差数列中的未知项
(1):3, a, 5;
(2):3, b, c,-9;
例1 (1 )已知数列{ an }的通项公式是an =3n-1,
求证:{an}为等差数列;
(2) 已知数列{an}是等差数列,
求证:数列{an+an+1} 也是等差数列.
【小结】
①数列{ an }为等差数列 ;
②证明一个数列为等差数列的方法是 :
.
an=kn+b
k、b是常数.
证明: an+1 — an为一个常数.
例题分析
例2 (1)等差数列11,8,5,…,的第19项是 ;
(2)等差数列-5,-9,-13,…的第 项是-307;
(3)已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4)已知{an}为等差数列,若a17= ,d= ,则
a10= .
-49
99
13
【说明】在等差数列{an}的通项公式中a1、d、an、n
任知 个,可求 .
三
另外一个
等 差 数 列
定义:按一定次序排列的一列数叫数列
(3)数列中的数是有顺序的,而数集合的数是无序的。
(2)数列中的数是可重复的,而数集中的数是互异的。
(1)数列与数集都是具有某种共同属性的 数的全体。
知识回顾
数列与数集有何区别和联系
数列
分类:项数有限的数列叫有穷数列;
项:数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(或首相),第2项,······,第n项, ······
数列分类
数列的项、首项
项数无限的数列叫做无穷数列。
数列的一般形式可以写成:
a1,a2,…,an,… 简记为{an}。
{an}是一个数列,而an是数列的第n项。
{an}与 an 的区别
数列一般形式
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
数列的通项公式的定义
函数与数列的联系
数列实质: 从函数的观点看,数列可以看作是自变量取值集合是正整数集 N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,通项公式即相应的函数解析式。
x
y
n
an
自变量
函数值
课堂练习
已知数列{an}的前四项是:9 ,4, —1,……,
则数列{an}的通项公式an = ,
2. 数列1,1,2,3,5,8,13,x,34,55,…中的x
等于( )
A. 19 B. 20 C. 21 D. 22
an+2= an+1+an
C
3. 已知数列{an}的前四项是:1 ,-3, 5,-7,……,
则-101在不在数列{an}中 ,
不在
14 - 5n
4. 上面几个数列,它们有没有规律
阅读课本33-34页并弄清:
1.什么样的数列是等差数列?
2.什么是等差数列的公差?
3.等差数列相邻两项与公差的关系
4.等差数列连续三项之间的关系
5.等差数列的通项公式是什么
6.等差数列的图象的特征是什么?
③推导等差数列通项公式的方法叫做 法.
递推
每一项与
它前一项的差
学习新课
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
①数列{ an }为等差数列 ;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
由定义归纳通项公式
a2 - a1=d,
a3 - a2=d,
a4 - a3=d,
……
则 a2=a1+d
a3=a2+d=a1+2d
a4=a3+d=a1+3d
……
由此得到 a n=a1+(n-1)d
an-1-an-2=d,
an -an-1=d.
这(n-1)个式子迭加
an - a1= (n-1)d
当n=1时,上式两边均等于a1,即等式也成立的。这表明当n∈N*时上式都成立,因而它就是等差数列{an}的通项公式。
判定下列数列是否可能是等差数列?
1. 9 ,8,7,6,5,4,……;
2. 1,1,1,1,……;
3. 1,0,1,0,1,……;
4. 0,2,3,4,5,……;
5. m, m, m, m, ……;
6. 1,11,21,31,41,…….
√
√
√
√
×
×
课堂练习
2.判断题:
①数列a,2a,3a,4a,…是等差数列( )
②若an-an+1=3 (n∈N*),则{an}是公差为3
的等差数列。 ( )
若a2-a1=a3-a2, 则数列{an}是等差数
列 ( )
1、等差数列要求从第2项起,后一项与
前一项作差。 不能颠倒。
2、作差的结果要求是同一个常数。
可以是整数,也可以是0和负数。
③
对等差数列的定义的理解
1.如果一个数列,不是从第2项起,而是
从第3项起或第4项起,每一项与它前一
项的差是同一个常数,那 么这个数列不
是等差数列.
2.一个数列从第2项起,每一项与它前一
项的差尽管等于常数,这个数列也不一
定是等差数列,因为这些常数不一定相
同.当这些常数不同时,此数列不是等
差数列
对等差数列的定义的理解
3.求公差时,要注意相邻两项相减的顺序
d=an+1-an或d=an-an-1(n≥2)
4. 要判断一个数列是不是等差数列,只要
看对于任意正整数n,an-an-1,是不是通
一个常数,切记不可通过计算a2-a1,a3-a2
等有限的几个式子的值后,发现它一个
常数,就得出该数列为等差数列的结论
等差中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等差数列:
(1)2 , , 4 (2)-1, ,5
(3)-12, ,0 (4)0, ,0
3
2
-6
0
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
求出下列等差数列中的未知项
(1):3, a, 5;
(2):3, b, c,-9;
例1 (1 )已知数列{ an }的通项公式是an =3n-1,
求证:{an}为等差数列;
(2) 已知数列{an}是等差数列,
求证:数列{an+an+1} 也是等差数列.
【小结】
①数列{ an }为等差数列 ;
②证明一个数列为等差数列的方法是 :
.
an=kn+b
k、b是常数.
证明: an+1 — an为一个常数.
例题分析
例2 (1)等差数列11,8,5,…,的第19项是 ;
(2)等差数列-5,-9,-13,…的第 项是-307;
(3)已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4)已知{an}为等差数列,若a17= ,d= ,则
a10= .
-49
99
13
【说明】在等差数列{an}的通项公式中a1、d、an、n
任知 个,可求 .
三
另外一个
