2.2等差数列课件2(苏教版必修5)
图片预览






文档简介
(共18张PPT)
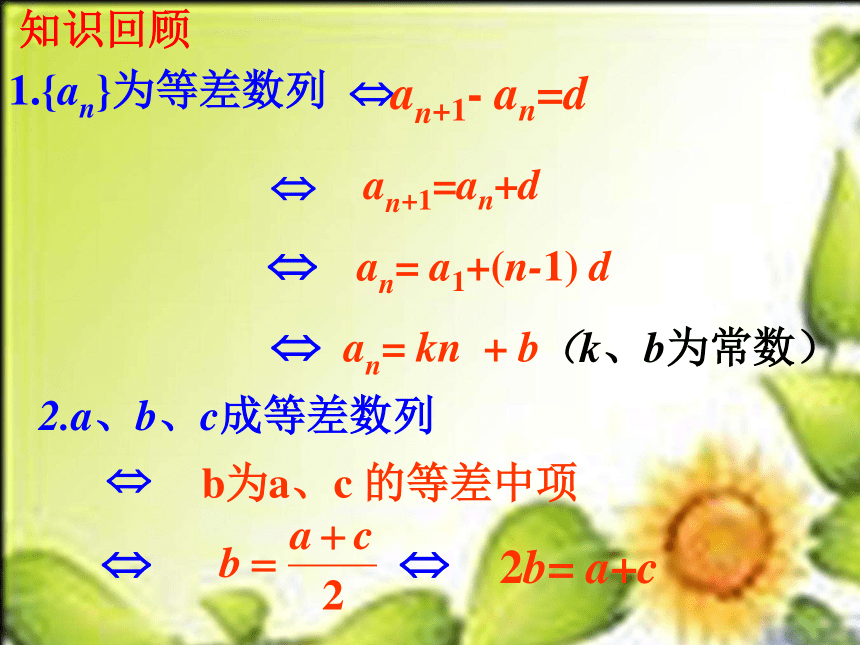
2.a、b、c成等差数列
2b= a+c
1.{an}为等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
b为a、c 的等差中项
知识回顾
结论归纳:
数列{an}是公差为d 的等差数列。
数列a1,a3,a5,a7,……是公差为 等差数列
数列a2,a4,a6,a8,……是公差为 等差数列
数列ma2,ma4,ma6,ma8,……是公差为 等差数列
数列a1+a2, a2+a3, a3+a4, a3+a4,……是公差
为 等差数列
2d
2d
2md
2d
等差数列的性质
1.
2.
3.
②上面的命题中的等式两边有 相 同 数 目 的项,如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
am+(n - m) d
4.在等差数列{an}中,由 m+n=p+q
m,n,p,q∈N★
am+an=ap+aq
注意:①上面的命题的逆命题 是不一定成立 的;
5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …
=
=
=
课本P37. 1, 2. 3 ,4,5,
课堂练习
由练习1可知:对于数列a1,a2,a3,a4,……
观察其规律,可以写出通项公式
例如:数列9,99,999,9999,……观察其规律,
可以写出通项公式
那么:数列1,11,111,1111,……观察其规律,
可以写出通项公式
例 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
例题分析
(2)已知 a3+a11=10,求 a6+a7+a8
分析:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数.
已知{an}为等差数列
且 a4+a5+a6+a7=56,a4a7=187,求公差d.
解:a1=1,
a1=4
a2=5=a1+1
a3=6=a2+1
…………
an=an-1+1 (2≤n≤7)
定义:已知数列{an}的第1项(或前几 项),且任意一项an与前一项an-1(或前几项)间的关系可以用一个公式来表示,那么这个公式叫做数列的递推公式
Sn法:若数列的前n项和记为Sn,即
Sn=a1+a2+a3+……+an-1+an
Sn-1
∴当n≥2时,有an=Sn-Sn-1
例.已知{an}的前 n项和Sn=n2+n-2 ,求an.
解:当n≥2时,an=Sn-Sn-1
=n2+n-2-(n-1)2-(n-1) +2
=2n
当n=1时,a1=0
1.若Sn=n2-1,求an
2.若Sn=2n2-3n,求an
在某个活动中,学校为烘托节日气氛,在200米长的校园主干道一侧,从起点开始,每隔3米插一面彩旗,由近及远排成一列,迎风飘扬。问最后一面旗子会插在终点处吗?一共应插多少面旗子?
0
3
6
9
200
……
若从距离起点2米开始,每隔3米插一面彩旗,则在距离起点80米处是否应该插旗?若是,是第几面旗子?
2
5
8
11
80
…
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
n
↓
↓
答:应该插第27面旗子
①前100个自然数的和:1+2+3+…+100= ;
②前n个偶数的和:2+4+6+…+2n= .
思考题:如何求下列和?
n(n+1)
2.a、b、c成等差数列
2b= a+c
1.{an}为等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
b为a、c 的等差中项
知识回顾
结论归纳:
数列{an}是公差为d 的等差数列。
数列a1,a3,a5,a7,……是公差为 等差数列
数列a2,a4,a6,a8,……是公差为 等差数列
数列ma2,ma4,ma6,ma8,……是公差为 等差数列
数列a1+a2, a2+a3, a3+a4, a3+a4,……是公差
为 等差数列
2d
2d
2md
2d
等差数列的性质
1.
2.
3.
②上面的命题中的等式两边有 相 同 数 目 的项,如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
am+(n - m) d
4.在等差数列{an}中,由 m+n=p+q
m,n,p,q∈N★
am+an=ap+aq
注意:①上面的命题的逆命题 是不一定成立 的;
5. 在等差数列{an}中a1+an a2+ an-1 a3+ an-2 …
=
=
=
课本P37. 1, 2. 3 ,4,5,
课堂练习
由练习1可知:对于数列a1,a2,a3,a4,……
观察其规律,可以写出通项公式
例如:数列9,99,999,9999,……观察其规律,
可以写出通项公式
那么:数列1,11,111,1111,……观察其规律,
可以写出通项公式
例 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
例题分析
(2)已知 a3+a11=10,求 a6+a7+a8
分析:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数.
已知{an}为等差数列
且 a4+a5+a6+a7=56,a4a7=187,求公差d.
解:a1=1,
a1=4
a2=5=a1+1
a3=6=a2+1
…………
an=an-1+1 (2≤n≤7)
定义:已知数列{an}的第1项(或前几 项),且任意一项an与前一项an-1(或前几项)间的关系可以用一个公式来表示,那么这个公式叫做数列的递推公式
Sn法:若数列的前n项和记为Sn,即
Sn=a1+a2+a3+……+an-1+an
Sn-1
∴当n≥2时,有an=Sn-Sn-1
例.已知{an}的前 n项和Sn=n2+n-2 ,求an.
解:当n≥2时,an=Sn-Sn-1
=n2+n-2-(n-1)2-(n-1) +2
=2n
当n=1时,a1=0
1.若Sn=n2-1,求an
2.若Sn=2n2-3n,求an
在某个活动中,学校为烘托节日气氛,在200米长的校园主干道一侧,从起点开始,每隔3米插一面彩旗,由近及远排成一列,迎风飘扬。问最后一面旗子会插在终点处吗?一共应插多少面旗子?
0
3
6
9
200
……
若从距离起点2米开始,每隔3米插一面彩旗,则在距离起点80米处是否应该插旗?若是,是第几面旗子?
2
5
8
11
80
…
↓ ↓ ↓ ↓
↓ ↓ ↓ ↓
n
↓
↓
答:应该插第27面旗子
①前100个自然数的和:1+2+3+…+100= ;
②前n个偶数的和:2+4+6+…+2n= .
思考题:如何求下列和?
n(n+1)
