2.2等差数列课件3(苏教版必修5)
图片预览





文档简介
(共13张PPT)
高一数学备课组
③推导等差数列通项公式的方法叫做 法.
递推
每一项与
它前一项的差
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
①数列{ an }为等差数列 ;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
知识回顾
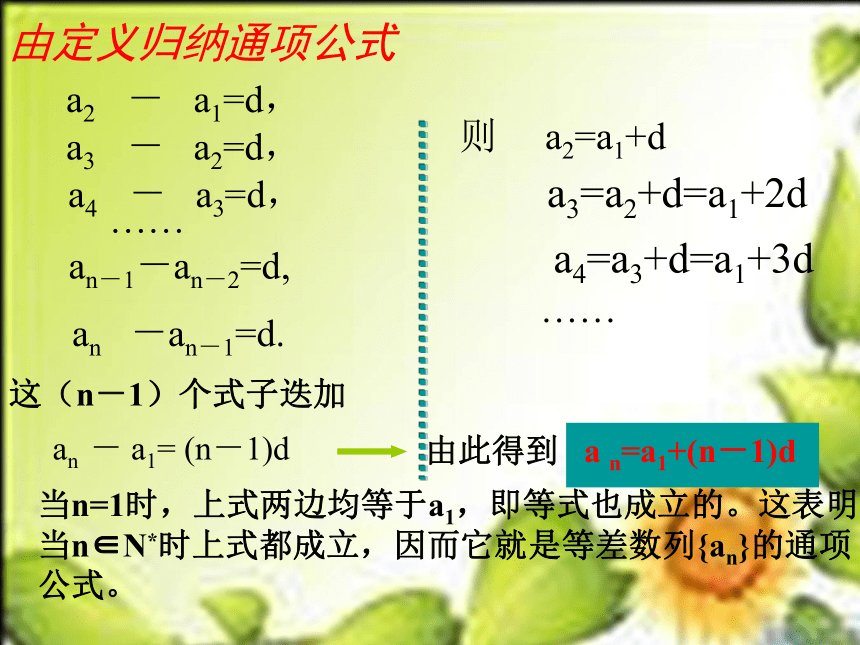
由定义归纳通项公式
a2 - a1=d,
a3 - a2=d,
a4 - a3=d,
……
则 a2=a1+d
a3=a2+d=a1+2d
a4=a3+d=a1+3d
……
由此得到 a n=a1+(n-1)d
an-1-an-2=d,
an -an-1=d.
这(n-1)个式子迭加
an - a1= (n-1)d
当n=1时,上式两边均等于a1,即等式也成立的。这表明当n∈N*时上式都成立,因而它就是等差数列{an}的通项公式。
等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
课本P35. 2. 3 ,4,5,
课堂练习
结论归纳:
数列{an}是公差为d 的等差数列。
数列a1,a3,a5,a7,……是公差为 等差数列
数列a2,a4,a6,a8,……是公差为 等差数列
数列ma2,ma4,ma6,ma8,……是公差
为 等差数列
例1 (1 )已知数列{ an }的通项公式是an =3n-1,
求证:{an}为等差数列;
(2) 已知数列{an}是等差数列,
求证:数列{an+an+1} 也是等差数列.
【小结】
①数列{ an }为等差数 ;
②证明一个数列为等差数列的方法是 :
.
an=kn+b
k、b是常数.
证明: an+1 — an为一个常数.
例题分析
例2 (1)等差数列11,8,5,…,的第19项是 ;
(2)等差数列-5,-9,-13,…的第 项是-307;
(3)已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4)已知{an}为等差数列,若a17= ,d= ,则
a10= .
-49
99
13
【说明】在等差数列{an}的通项公式中a1、d、an、n
任知 个,可求 .
三
另外一个
上面的命题中的等式两边有 相 同 数 目 的项,如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
等差数列的性质1
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项AA
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
例3 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
例题分析
(2)已知 a3+a11=10,求 a6+a7+a8
分析:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数.
已知{an}为等差数列
且 a4+a5+a6+a7=56,a4a7=187,求公差d.
高一数学备课组
③推导等差数列通项公式的方法叫做 法.
递推
每一项与
它前一项的差
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
. . . . .
【说明】
①数列{ an }为等差数列 ;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是 的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
知识回顾
由定义归纳通项公式
a2 - a1=d,
a3 - a2=d,
a4 - a3=d,
……
则 a2=a1+d
a3=a2+d=a1+2d
a4=a3+d=a1+3d
……
由此得到 a n=a1+(n-1)d
an-1-an-2=d,
an -an-1=d.
这(n-1)个式子迭加
an - a1= (n-1)d
当n=1时,上式两边均等于a1,即等式也成立的。这表明当n∈N*时上式都成立,因而它就是等差数列{an}的通项公式。
等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
课本P35. 2. 3 ,4,5,
课堂练习
结论归纳:
数列{an}是公差为d 的等差数列。
数列a1,a3,a5,a7,……是公差为 等差数列
数列a2,a4,a6,a8,……是公差为 等差数列
数列ma2,ma4,ma6,ma8,……是公差
为 等差数列
例1 (1 )已知数列{ an }的通项公式是an =3n-1,
求证:{an}为等差数列;
(2) 已知数列{an}是等差数列,
求证:数列{an+an+1} 也是等差数列.
【小结】
①数列{ an }为等差数 ;
②证明一个数列为等差数列的方法是 :
.
an=kn+b
k、b是常数.
证明: an+1 — an为一个常数.
例题分析
例2 (1)等差数列11,8,5,…,的第19项是 ;
(2)等差数列-5,-9,-13,…的第 项是-307;
(3)已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4)已知{an}为等差数列,若a17= ,d= ,则
a10= .
-49
99
13
【说明】在等差数列{an}的通项公式中a1、d、an、n
任知 个,可求 .
三
另外一个
上面的命题中的等式两边有 相 同 数 目 的项,如a1+a2=a3 成立吗?
【说明】
3.更一般的情形,an= ,d=
等差数列的性质1
1. {an}为等差数列
2. a、b、c成等差数列
an+1- an=d
an+1=an+d
an= a1+(n-1) d
an= kn + b
(k、b为常数)
am+(n - m) d
b为a、c 的等差中项AA
2b= a+c
4.在等差数列{an}中,由 m+n=p+q
am+an=ap+aq
例3 .在等差数列{an}中
(1) 已知 a6+a9+a12+a15=20,求a1+a20
例题分析
(2)已知 a3+a11=10,求 a6+a7+a8
分析:由 a1+a20 =a6+ a15 = a9 +a12
及 a6+a9+a12+a15=20,可得a1+a20=10
分析: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15
三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数.
已知{an}为等差数列
且 a4+a5+a6+a7=56,a4a7=187,求公差d.
