第6章数据的收集与描述
图片预览






文档简介
(共19张PPT)
第一节 数据的收集
1.收集数据有以下几个过程:
第一步:明确调查目的
第二步:确定调查对象
第三步:选择调查方法
第四步:具体进行调查
第五步:记录调查结果
2.在日常生活、生产和科学研究中,人们经常需要有目的地收集数据,以掌握有关的信息,做出明智的决策和判断。
如:篮球赛罚球数据
学生生长情况
新药的临床试验
第五次人口普查
观察
测量
调查
实验
数据收集的方法:
直接方法:直接观察、测量、调查、和实验等;
间接方法:查阅文献资料、使用互联网查询等。
等
有所发展是一个人成长的追求
第二节 统计图
掌握内容
条形统计图、复式折线统计图、扇形统计图的特点,优势。
注意统计图的选择
1.复式折线统计图
两张单式折线统计图叠放在一起就构成复式折线统计图。由复式折线统计图,不仅可以直观地比较两个或两个以上对象的发展变化趋势及各阶段数量的多少,而且可以直观地比较它们的数量增减变化的情况。
在画复式折线统计图时,要注意以下几个问题:
首先画两条互相垂直的数轴,横轴和纵分别表示不同的两个量。(注:两轴的单位长度可不同,但要注意各轴的单位长度要相等,同时,要标明表示的量和单位)
其次,要用不同颜色或虚实线表示不同意义的量。
第三、描点和连线准确。
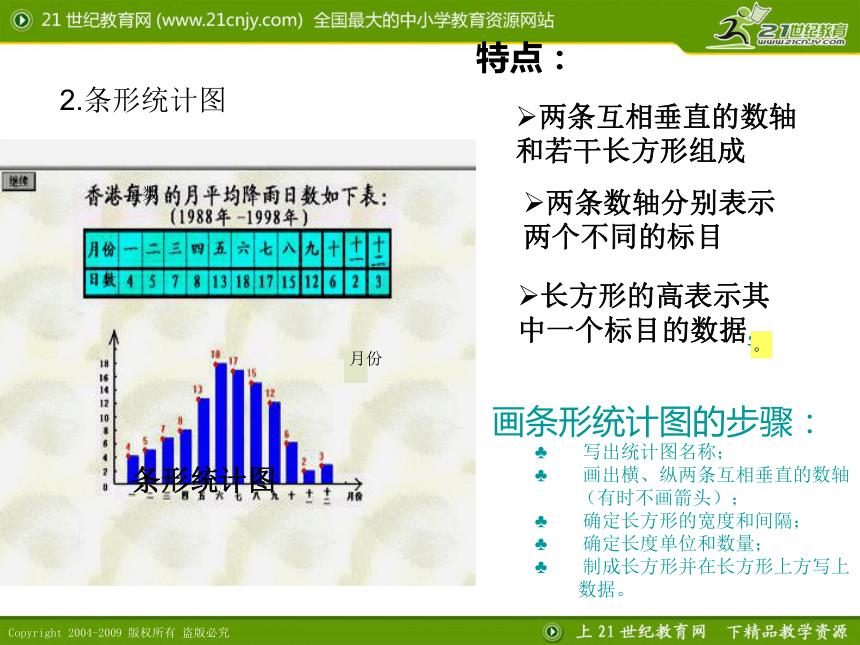
特点:
条形统计图
两条互相垂直的数轴和若干长方形组成
日数
月份
两条数轴分别表示两个不同的标目
长方形的高表示其中一个标目的数据.
。
画条形统计图的步骤:
写出统计图名称;
画出横、纵两条互相垂直的数轴(有时不画箭头);
确定长方形的宽度和间隔;
确定长度单位和数量;
制成长方形并在长方形上方写上数据。
2.条形统计图
(1)、统计图的特点:
1)、圆代表总体;
2)、扇形代表总体中的不同部分;
3)、扇形的大小反映部分占总体的百分比的大小.
(2)、各个扇形所占的百分比之和为1;
(3)、在不同的统计图中,不能简单地根据百分比的大小来比较部分量的大小。
2 .扇形统计图
一、想一想
1、通过学均数、中位数、众数各是什
么样的特征数?他们有什么联系?
分别怎样来求他们?
A、都可以作为一组数据的代表。
B、平均数比较可靠和稳定,它包括所有数据提供的
信息。因而应用最为广泛。但计算比较麻烦,容
易受到极端数的影响。
C、众数可靠性差,但其大小只与这组数据中部分数
据有关。计算简单,在一组数据中有不少数据重
复出现时,常选用它来 表示这组数据的集中趋势。
D、中位数可靠性也差,它与数据 的排序有关,不受
极端数据的影响,计算简单,当一组数据中个别
数据变动较大时,适合用中位数表示。
第三节 平均数 中位数 众数
知识点
平均数
(算术平均数与加权平均数)
中位数
众数
结构
实际背景
平均数
中位 数
众数
计算及应用
知识与结构
例题与练习
1.为了了解八年级学生的肥胖状况,随机抽查了20名学生,他们的体重(单位:千克)如下: 50 35 50 40 40 40 45 55 60 50 40 40 45 40 45 40 30 40 40 40
① 这20名学生体重的平均数、中位数、众数分别是多少?
② 你能估计出该年级的平均体重吗?并就此评价该年级学生的肥胖状况。
2. 下图反映了八年级(3)班40名学生在一次数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位数和众数。
② 根据图形估计这个班这次数学测验成绩的平均成绩。
3. 某政府部门招聘公务员1人,对前来应聘的A,B,C三人进行了三项测试.他们的各项测试成绩如下表所示,
① 根据三项测试的平均成绩确定录用人选,那么谁将被录用
② 若将笔试、面试、群众评议三项测试得分按1:2:4的比例确定各人的测试成绩,此时谁将被录用?
测试项目 测试成绩
A B C
笔 试 90 80 75
面 试 85 85 85
群众评议 77 84 80
练一练 1.(黑龙江)一组数据5,7,7,x,的中位数与平均 数相等,则x的值为
2.(甘肃)已知数据a,b,c,的平均数为8,那么a+1,b+2,c+3的平均数是
3.(重庆)某学校四个绿化小组,在植树节这天种下樟树的棵数如下:10,10,x,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是.
9或5
10
10
(2004年中考题)
4.(山东)已知一组数据5,15,75,45,25,75,45,35,45,35,
那么40是这一组数据的( ) A.平均数但不是中位数 B.平均数也是中位数 C. 众数 D.中位数但不是平均数
B
1、评定学生的学科期末成绩由期末考试分数, 作业分
数,课堂参与分数三部分组成, 并按3:3:4的比
例确定. 已知小明的数学期考80分, 作业90分,
课堂参与85分, 则他的数学期末成绩为 .
2、某校八年级有4个班,期中数学测验1班50人平
均68分,2班48人平均70分,3班50人平均72分,4
班52人平均70分,则该年级期中数学测验平均
为 分.
二、做一做
3、某校八年⑶班在一次数学测验中,有2人得
100分,4人得95分,2人得90分,6人得85分,4人
得80分,6得75分,5人得72分,5人得64分,4人得
60分,4人得55分,2人得50分,6人得40分,则该
班的数学成绩平均为 分.
4、数据 –2,0,2,3,4,2,5的中位数是 .
5. 数据 9,6,4,4,5,6,7,6,8,6的众数是 ,
中位数是 ,平均数是 .
6、一组数据13,18,15,x,14的平均数是14.8,
则x= ,众数是 ,中位数是 。
6. 某校八年级⑷班共47人,身高1.70米的有10
人,1.66米的有5人,1.6米的有15人,1.58
米的有10人,1.55米的有5人,1.50米的有2
人,则该班学生的身高的平均数为 ,
中位数为 ,众数为 .
7. 若数据4,6,x,8,12的平均数为8,则其中位
数为 .
8. 若数据5,-3,0,x,4,6的中位数为4,则其众
数为 .
二、做一做
9.某村有村民300人,其中年收入800元的有150人,
1500元的有100人, 2000元的有45人,还有5人年
收入100万元.根据这些数据计算该村人收入的
平均数,中位数,众数.你认为这个数据中哪一个
代表村民年收入的“平均水平”更合适?
10.某校八年级(2)班期末语文、数学、英语
的考试成绩依次比期中提高了10%,15%,5%。
现要计算这三科总的提高水平,张均同学用两
种方法计算平均数,你知道怎样计算吗?两种结
果,哪种能较好地反映这三科总的提高水平?
为什么?
三、议一议
11、下图反映了八年级(2)班40名学生在一次
数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位
数和众数。
② 根据图形估计这个班这次数学测验成绩的平
均成绩。
三、议一议
第一节 数据的收集
1.收集数据有以下几个过程:
第一步:明确调查目的
第二步:确定调查对象
第三步:选择调查方法
第四步:具体进行调查
第五步:记录调查结果
2.在日常生活、生产和科学研究中,人们经常需要有目的地收集数据,以掌握有关的信息,做出明智的决策和判断。
如:篮球赛罚球数据
学生生长情况
新药的临床试验
第五次人口普查
观察
测量
调查
实验
数据收集的方法:
直接方法:直接观察、测量、调查、和实验等;
间接方法:查阅文献资料、使用互联网查询等。
等
有所发展是一个人成长的追求
第二节 统计图
掌握内容
条形统计图、复式折线统计图、扇形统计图的特点,优势。
注意统计图的选择
1.复式折线统计图
两张单式折线统计图叠放在一起就构成复式折线统计图。由复式折线统计图,不仅可以直观地比较两个或两个以上对象的发展变化趋势及各阶段数量的多少,而且可以直观地比较它们的数量增减变化的情况。
在画复式折线统计图时,要注意以下几个问题:
首先画两条互相垂直的数轴,横轴和纵分别表示不同的两个量。(注:两轴的单位长度可不同,但要注意各轴的单位长度要相等,同时,要标明表示的量和单位)
其次,要用不同颜色或虚实线表示不同意义的量。
第三、描点和连线准确。
特点:
条形统计图
两条互相垂直的数轴和若干长方形组成
日数
月份
两条数轴分别表示两个不同的标目
长方形的高表示其中一个标目的数据.
。
画条形统计图的步骤:
写出统计图名称;
画出横、纵两条互相垂直的数轴(有时不画箭头);
确定长方形的宽度和间隔;
确定长度单位和数量;
制成长方形并在长方形上方写上数据。
2.条形统计图
(1)、统计图的特点:
1)、圆代表总体;
2)、扇形代表总体中的不同部分;
3)、扇形的大小反映部分占总体的百分比的大小.
(2)、各个扇形所占的百分比之和为1;
(3)、在不同的统计图中,不能简单地根据百分比的大小来比较部分量的大小。
2 .扇形统计图
一、想一想
1、通过学均数、中位数、众数各是什
么样的特征数?他们有什么联系?
分别怎样来求他们?
A、都可以作为一组数据的代表。
B、平均数比较可靠和稳定,它包括所有数据提供的
信息。因而应用最为广泛。但计算比较麻烦,容
易受到极端数的影响。
C、众数可靠性差,但其大小只与这组数据中部分数
据有关。计算简单,在一组数据中有不少数据重
复出现时,常选用它来 表示这组数据的集中趋势。
D、中位数可靠性也差,它与数据 的排序有关,不受
极端数据的影响,计算简单,当一组数据中个别
数据变动较大时,适合用中位数表示。
第三节 平均数 中位数 众数
知识点
平均数
(算术平均数与加权平均数)
中位数
众数
结构
实际背景
平均数
中位 数
众数
计算及应用
知识与结构
例题与练习
1.为了了解八年级学生的肥胖状况,随机抽查了20名学生,他们的体重(单位:千克)如下: 50 35 50 40 40 40 45 55 60 50 40 40 45 40 45 40 30 40 40 40
① 这20名学生体重的平均数、中位数、众数分别是多少?
② 你能估计出该年级的平均体重吗?并就此评价该年级学生的肥胖状况。
2. 下图反映了八年级(3)班40名学生在一次数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位数和众数。
② 根据图形估计这个班这次数学测验成绩的平均成绩。
3. 某政府部门招聘公务员1人,对前来应聘的A,B,C三人进行了三项测试.他们的各项测试成绩如下表所示,
① 根据三项测试的平均成绩确定录用人选,那么谁将被录用
② 若将笔试、面试、群众评议三项测试得分按1:2:4的比例确定各人的测试成绩,此时谁将被录用?
测试项目 测试成绩
A B C
笔 试 90 80 75
面 试 85 85 85
群众评议 77 84 80
练一练 1.(黑龙江)一组数据5,7,7,x,的中位数与平均 数相等,则x的值为
2.(甘肃)已知数据a,b,c,的平均数为8,那么a+1,b+2,c+3的平均数是
3.(重庆)某学校四个绿化小组,在植树节这天种下樟树的棵数如下:10,10,x,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是.
9或5
10
10
(2004年中考题)
4.(山东)已知一组数据5,15,75,45,25,75,45,35,45,35,
那么40是这一组数据的( ) A.平均数但不是中位数 B.平均数也是中位数 C. 众数 D.中位数但不是平均数
B
1、评定学生的学科期末成绩由期末考试分数, 作业分
数,课堂参与分数三部分组成, 并按3:3:4的比
例确定. 已知小明的数学期考80分, 作业90分,
课堂参与85分, 则他的数学期末成绩为 .
2、某校八年级有4个班,期中数学测验1班50人平
均68分,2班48人平均70分,3班50人平均72分,4
班52人平均70分,则该年级期中数学测验平均
为 分.
二、做一做
3、某校八年⑶班在一次数学测验中,有2人得
100分,4人得95分,2人得90分,6人得85分,4人
得80分,6得75分,5人得72分,5人得64分,4人得
60分,4人得55分,2人得50分,6人得40分,则该
班的数学成绩平均为 分.
4、数据 –2,0,2,3,4,2,5的中位数是 .
5. 数据 9,6,4,4,5,6,7,6,8,6的众数是 ,
中位数是 ,平均数是 .
6、一组数据13,18,15,x,14的平均数是14.8,
则x= ,众数是 ,中位数是 。
6. 某校八年级⑷班共47人,身高1.70米的有10
人,1.66米的有5人,1.6米的有15人,1.58
米的有10人,1.55米的有5人,1.50米的有2
人,则该班学生的身高的平均数为 ,
中位数为 ,众数为 .
7. 若数据4,6,x,8,12的平均数为8,则其中位
数为 .
8. 若数据5,-3,0,x,4,6的中位数为4,则其众
数为 .
二、做一做
9.某村有村民300人,其中年收入800元的有150人,
1500元的有100人, 2000元的有45人,还有5人年
收入100万元.根据这些数据计算该村人收入的
平均数,中位数,众数.你认为这个数据中哪一个
代表村民年收入的“平均水平”更合适?
10.某校八年级(2)班期末语文、数学、英语
的考试成绩依次比期中提高了10%,15%,5%。
现要计算这三科总的提高水平,张均同学用两
种方法计算平均数,你知道怎样计算吗?两种结
果,哪种能较好地反映这三科总的提高水平?
为什么?
三、议一议
11、下图反映了八年级(2)班40名学生在一次
数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位
数和众数。
② 根据图形估计这个班这次数学测验成绩的平
均成绩。
三、议一议
同课章节目录
