2020-2021学年下学期华东师大版八年级数学下册 17.5 实践与探索(培优卷)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年下学期华东师大版八年级数学下册 17.5 实践与探索(培优卷)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 373.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 15:45:55 | ||
图片预览



文档简介
17.5
实践与探索(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为(
)
A.(﹣4,0)
B.(6,0)
C.(﹣4,0)或(6,0)
D.无法确定
2.已知直线y=-x+4与y=x+2如图所示,则方程组的解为(
)
A.
B.
C.
D.
3.一根弹簧原长12
cm,它所挂的重量不超过10
kg,并且挂重1
kg就伸长1.5
cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )
A.y=1.5(x+12)(0≤x≤10)
B.y=1.5x+12(0≤x≤10)
C.y=1.5x+12(x≥0)
D.y=1.5(x-12)(0≤x≤10)
4.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式kx+b>0的的解集为(
)
A.>–2
B.<–2
C.
D.
5.若方程组没有解,则一次函数y=2-x与y=-x的图像必定(
)
A.重合
B.平行
C.相交
D.无法确定
6.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为(
)
A.x=-1
B.x=0
C.x=-2.
D.x=1
7.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打6折,设购买种子数量为千克,付款金额为元,则与的函数关系的图像大致是
(
)
A.
B.
C.
D.
8.一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是(
)
A.甲乙两地相距1200千米
B.快车的速度是80千米∕小时
C.慢车的速度是60千米/小时
D.快车到达甲地时,慢车距离乙地100千米
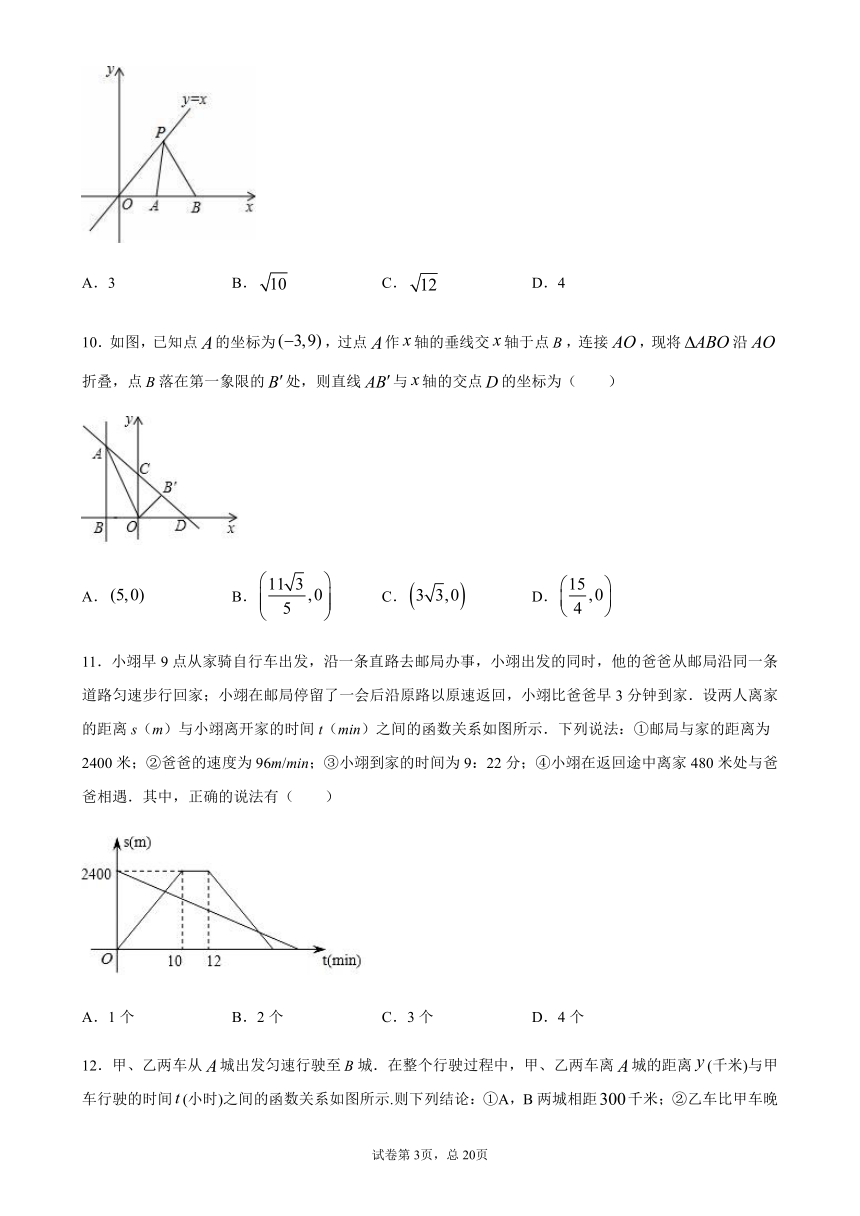
9.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(3,0)是x轴上的两点,则PA+PB的最小值为( )
A.3
B.
C.
D.4
10.如图,已知点的坐标为,过点作轴的垂线交轴于点,连接,现将沿折叠,点落在第一象限的处,则直线与轴的交点的坐标为(
)
A.
B.
C.
D.
11.小翊早9点从家骑自行车出发,沿一条直路去邮局办事,小翊出发的同时,他的爸爸从邮局沿同一条道路匀速步行回家;小翊在邮局停留了一会后沿原路以原速返回,小翊比爸爸早3分钟到家.设两人离家的距离s(m)与小翊离开家的时间t(min)之间的函数关系如图所示.下列说法:①邮局与家的距离为2400米;②爸爸的速度为96m/min;③小翊到家的时间为9:22分;④小翊在返回途中离家480米处与爸爸相遇.其中,正确的说法有( )
A.1个
B.2个
C.3个
D.4个
12.甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离城的距离(千米)与甲车行驶的时间(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距千米;②乙车比甲车晚出发小时,却早到小时;③乙车出发后小时追上甲车;④当甲、乙两车相距千米时,
其中正确的结论有(
)
A.个
B.个
C.个
D.个
二、填空题
13.某长途汽车公司规定旅客可免费随身携带一定质量的行李,若超过规定,则需购买行李票。行李票的费用y(元)是行李质量x(千克)的一次函数,其图象如图所示,则y与x之间的函数解析式是
,旅客最多可免费携带行李____千克。
14.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
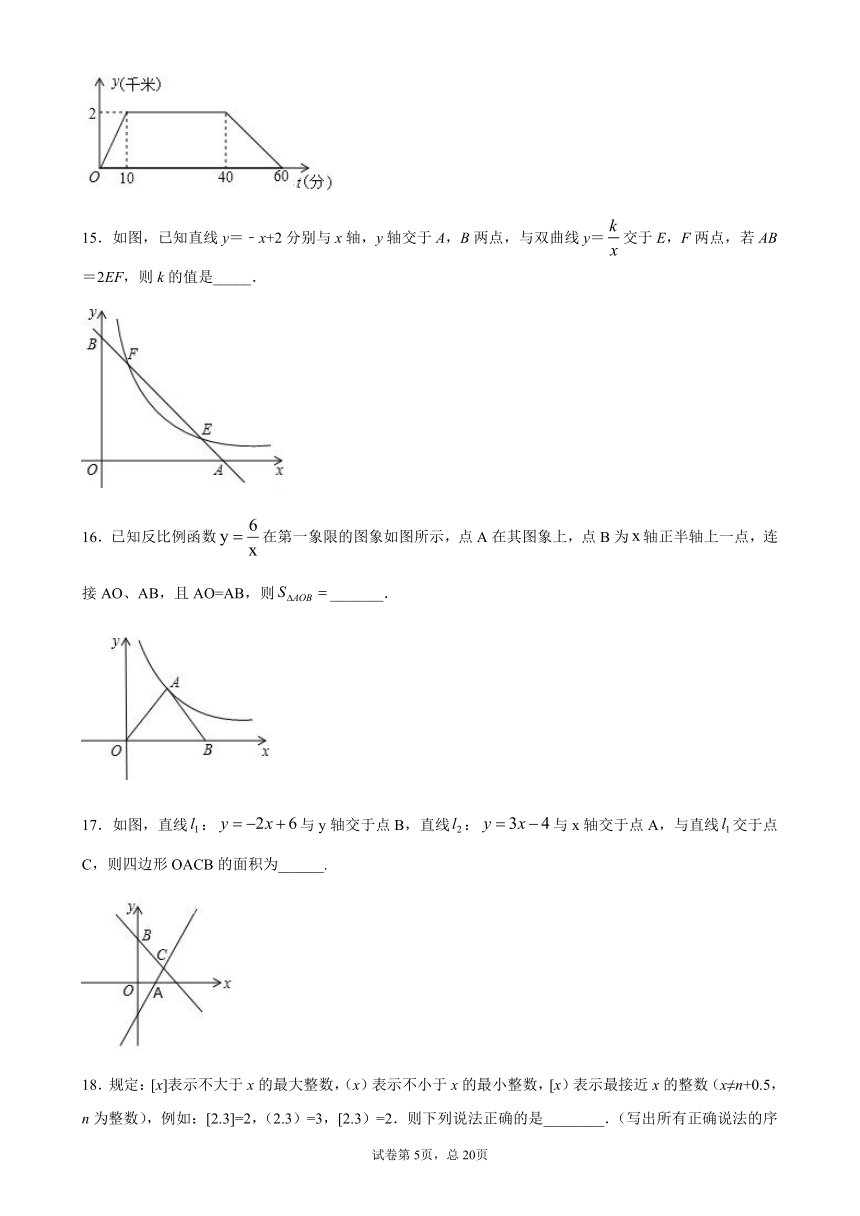
15.如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点,若AB=2EF,则k的值是_____.
16.已知反比例函数在第一象限的图象如图所示,点A在其图象上,点B为轴正半轴上一点,连接AO、AB,且AO=AB,则_______.
17.如图,直线:与y轴交于点B,直线:与x轴交于点A,与直线交于点C,则四边形OACB的面积为______.
18.规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
三、解答题
19.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.
(1)求反比例函数y=的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.
20.益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低.马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种
A
B
原来的运费
45
25
现在的运费
30
20
(1)求每次运输的农产品中A,B产品各有多少件;
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元.
21.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y
(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
22.如图,已知一次函数
的图象经过A
(-2,-1)
,
B
(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式
(2)△AOB的面积
23.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
24.如图,已知函数的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P
(a,0)(其中a>2),过点P作x轴的垂线,分别交函数和y=x的图象于点C,D
(1)求点A的坐标;
(2)若OB=CD,求a的值.
25.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是
千米/时,t=
小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
26.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
B
A
B
A
B
C
B
D
D
B
二、填空题
13
14
15
16
17
18
y=x-6;30
1.5
6
②③
三、解答题
19.
(1)将点A(4,3)代入y=,得:k=12,
则反比例函数解析式为y=;
(2)如图,过点A作AC⊥x轴于点C,
则OC=4、AC=3,
∴OA==5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
(3)∵点B坐标为(9,3),
∴OB所在直线解析式为y=x,
由可得点P坐标为(6,2),(负值舍去),
过点P作PD⊥x轴,延长DP交AB于点E,
则点E坐标为(6,3),
∴AE=2、PE=1、PD=2,
则△OAP的面积=×(2+6)×3﹣×6×2﹣×2×1=5.
20.
解:(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,
根据题意得:
,解得:,
答:每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,
增加供货量后A产品的数量为(10+m)件,B产品的数量为30+(8-m)=(38-m)件,
根据题意得:W=30(10+m)+20(38-m)=10m+1060,
由题意得:38-m≤2(10+m),
解得:m≥6,
即6≤m≤8,
∵一次函数W随m的增大而增大
∴当m=6时,W最小=1120,
答:产品件数增加后,每次运费最少需要1120元.
21.
解:(1)设线段AB解析式为y=k1x+b(k≠0)
∵线段AB过点(0,10),(2,14)
代入得
解得
∴AB解析式为:y=2x+10(0≤x<5)
∵B在线段AB上当x=5时,y=20
∴B坐标为(5,20)
∴线段BC的解析式为:y=20(5≤x<10)
设双曲线CD解析式为:y=(k2≠0)
∵C(10,20),
∴k2=200
∴双曲线CD解析式为:y=(10≤x≤24)
∴y关于x的函数解析式为:
(2)由(1)恒温系统设定恒温为20°C
(3)把y=10代入y=中,解得,x=20
∴20-10=10
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
22.
解:(1)把A(-2,-1),B(1,3)代入y=kx+b得
,解得,
所以一次函数解析式为;
(2)把x=0代入得,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD.
23.
解:(1)由图可知,A比B后出发1小时;B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设OC的解析式为s=kt,则3k=60,
解得k=20,
所以,s=20t,
设DE的解析式为s=mt+n,
则
,解得,
所以,s=45t﹣45,
由题意得,解得,
所以,B出发小时后两人相遇.
24.
解:(1)∵
点M在直线y=x的图象上,且点M的横坐标为2,
∴
点M的坐标为(2,2),
把M(2,2)代入y=﹣x+b得﹣1+b=2,解得b=3,
∴
一次函数的解析式为y=﹣x+3,
把y=0代入y=﹣x+3得﹣x+3=0,解得x=6,
∴
A点坐标为(6,0);
(2)把x=0代入y=﹣x+3得y=3,
∴
B点坐标为(0,3),
∵
CD=OB,
∴
CD=3,
∵
PC⊥x轴,
∴
C点坐标为(a,﹣a+3),D点坐标为(a,a)
∴
a﹣(﹣a+3)=3,
∴
a=4.
25.
解:(1)根据图示,可得
乙车的速度是60千米/时,
甲车的速度=720÷6=120(千米/小时)
∴t=360÷120=3(小时).
故答案为:60;3;
(2)①当0≤x≤3时,设y=k1x,
把(3,360)代入,可得:3k1=360,解得k1=120,
∴y=120x(0≤x≤3).
②当3<x≤4时,y=360.
③4<x≤7时,设y=k2x+b,
把(4,360)和(7,0)代入,可得,解得:
∴y=﹣120x+840(4<x≤7).
(3)①
300÷180+1=+1=(小时)
②当甲车停留在C地时,(小时)
③两车都朝A地行驶时,设乙车出发x小时后两车相距120千米,
则60x﹣[120(x﹣1)﹣360]=120,
所以480﹣60x=120,
所以60x=360,
解得x=6.
综上,可得乙车出发小时、4小时、6小时后两车相距120千米.
26.
解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E
∴∠CAD+∠DCA=90°
∵∠BAC=90°
∴∠CAD+∠BAE=90°
∴∠BAE=∠ACD
在和中
,
∴≌(AAS)
∴CD=AE,AD=BE
∵A(2,0)、B(3,3)
∴OA=2,OE=BE=3
∴CD=AE=1,OD=AD﹣OA=1
∴C的坐标是(﹣1,1)
(2)如图,作BE⊥x轴于E
设直线BC的解析式为y=kx+b
∵B点的坐标为(3,3),C点的坐标是(﹣1,1)
∴,解得,
∴直线BC的解析式为y=x+
当x=0时,y=
∴OM=
∴=×(+3)×3﹣×2×﹣×1×3=
(3)如图,作M关于x轴的对称点(0,﹣),连接B,交x轴于点P,此时PB+PM=PB+P=B的值最小
设直线B的解析式为y=mx+n
则,解得:
∴直线B的解析式为y=x﹣
点P在x轴上,当y=0时,x=1,
∴点P的坐标为(1,0).
试卷第2页,总2页
试卷第1页,总1页
实践与探索(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为(
)
A.(﹣4,0)
B.(6,0)
C.(﹣4,0)或(6,0)
D.无法确定
2.已知直线y=-x+4与y=x+2如图所示,则方程组的解为(
)
A.
B.
C.
D.
3.一根弹簧原长12
cm,它所挂的重量不超过10
kg,并且挂重1
kg就伸长1.5
cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )
A.y=1.5(x+12)(0≤x≤10)
B.y=1.5x+12(0≤x≤10)
C.y=1.5x+12(x≥0)
D.y=1.5(x-12)(0≤x≤10)
4.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式kx+b>0的的解集为(
)
A.>–2
B.<–2
C.
D.
5.若方程组没有解,则一次函数y=2-x与y=-x的图像必定(
)
A.重合
B.平行
C.相交
D.无法确定
6.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为(
)
A.x=-1
B.x=0
C.x=-2.
D.x=1
7.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打6折,设购买种子数量为千克,付款金额为元,则与的函数关系的图像大致是
(
)
A.
B.
C.
D.
8.一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是(
)
A.甲乙两地相距1200千米
B.快车的速度是80千米∕小时
C.慢车的速度是60千米/小时
D.快车到达甲地时,慢车距离乙地100千米
9.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(3,0)是x轴上的两点,则PA+PB的最小值为( )
A.3
B.
C.
D.4
10.如图,已知点的坐标为,过点作轴的垂线交轴于点,连接,现将沿折叠,点落在第一象限的处,则直线与轴的交点的坐标为(
)
A.
B.
C.
D.
11.小翊早9点从家骑自行车出发,沿一条直路去邮局办事,小翊出发的同时,他的爸爸从邮局沿同一条道路匀速步行回家;小翊在邮局停留了一会后沿原路以原速返回,小翊比爸爸早3分钟到家.设两人离家的距离s(m)与小翊离开家的时间t(min)之间的函数关系如图所示.下列说法:①邮局与家的距离为2400米;②爸爸的速度为96m/min;③小翊到家的时间为9:22分;④小翊在返回途中离家480米处与爸爸相遇.其中,正确的说法有( )
A.1个
B.2个
C.3个
D.4个
12.甲、乙两车从城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离城的距离(千米)与甲车行驶的时间(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距千米;②乙车比甲车晚出发小时,却早到小时;③乙车出发后小时追上甲车;④当甲、乙两车相距千米时,
其中正确的结论有(
)
A.个
B.个
C.个
D.个
二、填空题
13.某长途汽车公司规定旅客可免费随身携带一定质量的行李,若超过规定,则需购买行李票。行李票的费用y(元)是行李质量x(千克)的一次函数,其图象如图所示,则y与x之间的函数解析式是
,旅客最多可免费携带行李____千克。
14.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.
15.如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点,若AB=2EF,则k的值是_____.
16.已知反比例函数在第一象限的图象如图所示,点A在其图象上,点B为轴正半轴上一点,连接AO、AB,且AO=AB,则_______.
17.如图,直线:与y轴交于点B,直线:与x轴交于点A,与直线交于点C,则四边形OACB的面积为______.
18.规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
三、解答题
19.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.
(1)求反比例函数y=的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.
20.益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低.马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种
A
B
原来的运费
45
25
现在的运费
30
20
(1)求每次运输的农产品中A,B产品各有多少件;
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元.
21.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y
(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
22.如图,已知一次函数
的图象经过A
(-2,-1)
,
B
(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式
(2)△AOB的面积
23.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
24.如图,已知函数的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P
(a,0)(其中a>2),过点P作x轴的垂线,分别交函数和y=x的图象于点C,D
(1)求点A的坐标;
(2)若OB=CD,求a的值.
25.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是
千米/时,t=
小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
26.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
B
A
B
A
B
C
B
D
D
B
二、填空题
13
14
15
16
17
18
y=x-6;30
1.5
6
②③
三、解答题
19.
(1)将点A(4,3)代入y=,得:k=12,
则反比例函数解析式为y=;
(2)如图,过点A作AC⊥x轴于点C,
则OC=4、AC=3,
∴OA==5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
(3)∵点B坐标为(9,3),
∴OB所在直线解析式为y=x,
由可得点P坐标为(6,2),(负值舍去),
过点P作PD⊥x轴,延长DP交AB于点E,
则点E坐标为(6,3),
∴AE=2、PE=1、PD=2,
则△OAP的面积=×(2+6)×3﹣×6×2﹣×2×1=5.
20.
解:(1)设每次运输的农产品中A产品有x件,每次运输的农产品中B产品有y件,
根据题意得:
,解得:,
答:每次运输的农产品中A产品有10件,每次运输的农产品中B产品有30件,
(2)设增加m件A产品,则增加了(8-m)件B产品,设增加供货量后得运费为W元,
增加供货量后A产品的数量为(10+m)件,B产品的数量为30+(8-m)=(38-m)件,
根据题意得:W=30(10+m)+20(38-m)=10m+1060,
由题意得:38-m≤2(10+m),
解得:m≥6,
即6≤m≤8,
∵一次函数W随m的增大而增大
∴当m=6时,W最小=1120,
答:产品件数增加后,每次运费最少需要1120元.
21.
解:(1)设线段AB解析式为y=k1x+b(k≠0)
∵线段AB过点(0,10),(2,14)
代入得
解得
∴AB解析式为:y=2x+10(0≤x<5)
∵B在线段AB上当x=5时,y=20
∴B坐标为(5,20)
∴线段BC的解析式为:y=20(5≤x<10)
设双曲线CD解析式为:y=(k2≠0)
∵C(10,20),
∴k2=200
∴双曲线CD解析式为:y=(10≤x≤24)
∴y关于x的函数解析式为:
(2)由(1)恒温系统设定恒温为20°C
(3)把y=10代入y=中,解得,x=20
∴20-10=10
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
22.
解:(1)把A(-2,-1),B(1,3)代入y=kx+b得
,解得,
所以一次函数解析式为;
(2)把x=0代入得,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD.
23.
解:(1)由图可知,A比B后出发1小时;B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设OC的解析式为s=kt,则3k=60,
解得k=20,
所以,s=20t,
设DE的解析式为s=mt+n,
则
,解得,
所以,s=45t﹣45,
由题意得,解得,
所以,B出发小时后两人相遇.
24.
解:(1)∵
点M在直线y=x的图象上,且点M的横坐标为2,
∴
点M的坐标为(2,2),
把M(2,2)代入y=﹣x+b得﹣1+b=2,解得b=3,
∴
一次函数的解析式为y=﹣x+3,
把y=0代入y=﹣x+3得﹣x+3=0,解得x=6,
∴
A点坐标为(6,0);
(2)把x=0代入y=﹣x+3得y=3,
∴
B点坐标为(0,3),
∵
CD=OB,
∴
CD=3,
∵
PC⊥x轴,
∴
C点坐标为(a,﹣a+3),D点坐标为(a,a)
∴
a﹣(﹣a+3)=3,
∴
a=4.
25.
解:(1)根据图示,可得
乙车的速度是60千米/时,
甲车的速度=720÷6=120(千米/小时)
∴t=360÷120=3(小时).
故答案为:60;3;
(2)①当0≤x≤3时,设y=k1x,
把(3,360)代入,可得:3k1=360,解得k1=120,
∴y=120x(0≤x≤3).
②当3<x≤4时,y=360.
③4<x≤7时,设y=k2x+b,
把(4,360)和(7,0)代入,可得,解得:
∴y=﹣120x+840(4<x≤7).
(3)①
300÷180+1=+1=(小时)
②当甲车停留在C地时,(小时)
③两车都朝A地行驶时,设乙车出发x小时后两车相距120千米,
则60x﹣[120(x﹣1)﹣360]=120,
所以480﹣60x=120,
所以60x=360,
解得x=6.
综上,可得乙车出发小时、4小时、6小时后两车相距120千米.
26.
解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E
∴∠CAD+∠DCA=90°
∵∠BAC=90°
∴∠CAD+∠BAE=90°
∴∠BAE=∠ACD
在和中
,
∴≌(AAS)
∴CD=AE,AD=BE
∵A(2,0)、B(3,3)
∴OA=2,OE=BE=3
∴CD=AE=1,OD=AD﹣OA=1
∴C的坐标是(﹣1,1)
(2)如图,作BE⊥x轴于E
设直线BC的解析式为y=kx+b
∵B点的坐标为(3,3),C点的坐标是(﹣1,1)
∴,解得,
∴直线BC的解析式为y=x+
当x=0时,y=
∴OM=
∴=×(+3)×3﹣×2×﹣×1×3=
(3)如图,作M关于x轴的对称点(0,﹣),连接B,交x轴于点P,此时PB+PM=PB+P=B的值最小
设直线B的解析式为y=mx+n
则,解得:
∴直线B的解析式为y=x﹣
点P在x轴上,当y=0时,x=1,
∴点P的坐标为(1,0).
试卷第2页,总2页
试卷第1页,总1页
