北师大版九年级下数学课件 3.7 切线长定理(19张)
文档属性
| 名称 | 北师大版九年级下数学课件 3.7 切线长定理(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览



文档简介
27.2 与圆有关的位置关系
第4课时 切线长定理与
三角形的内切圆
复习回顾
3.如图:在⊙O中,OA、OB为半径,直线MN与
⊙O相切于点B,若∠ABN=30°,则∠AOB= .
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
60°
预习检测
1、切线长定理:1、过圆外一点所画的圆的两条切线,它们的切线长 .
2、这一点和圆心的连线 这两条切线的夹角。
相等
平分
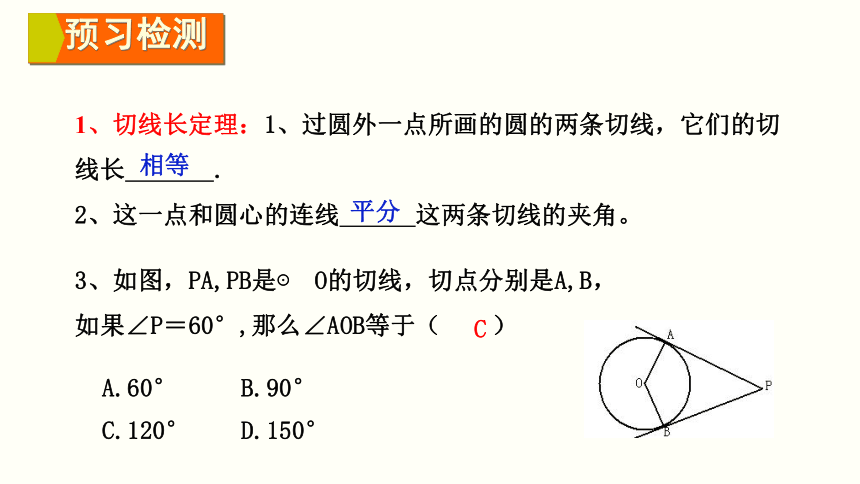
3、如图,PA,PB是⊙ O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A.60° B.90°
C.120° D.150°
C
情境导入
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
B
A
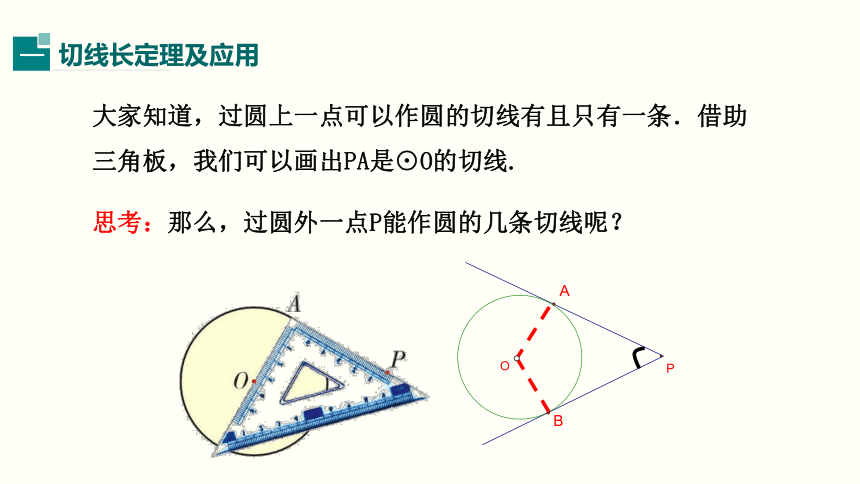
大家知道,过圆上一点可以作圆的切线有且只有一条.借助三角板,我们可以画出PA是⊙O的切线.
思考:那么,过圆外一点P能作圆的几条切线呢?
O
P
切线长定理及应用
一
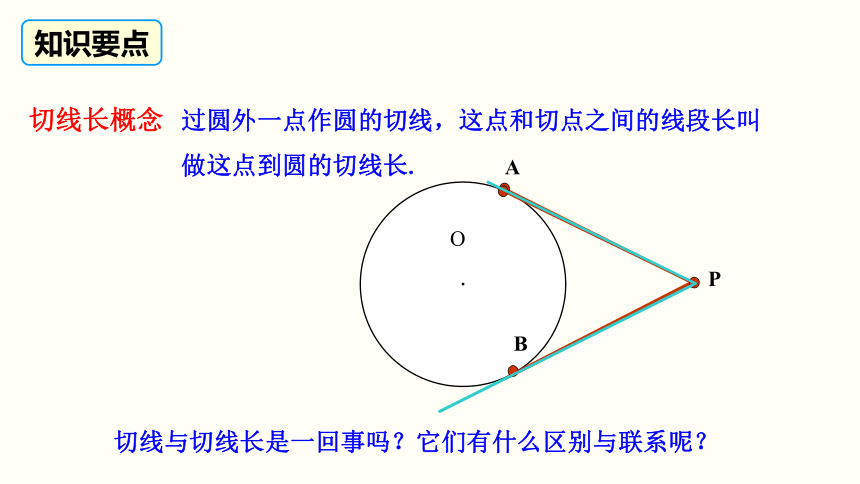
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
知识要点
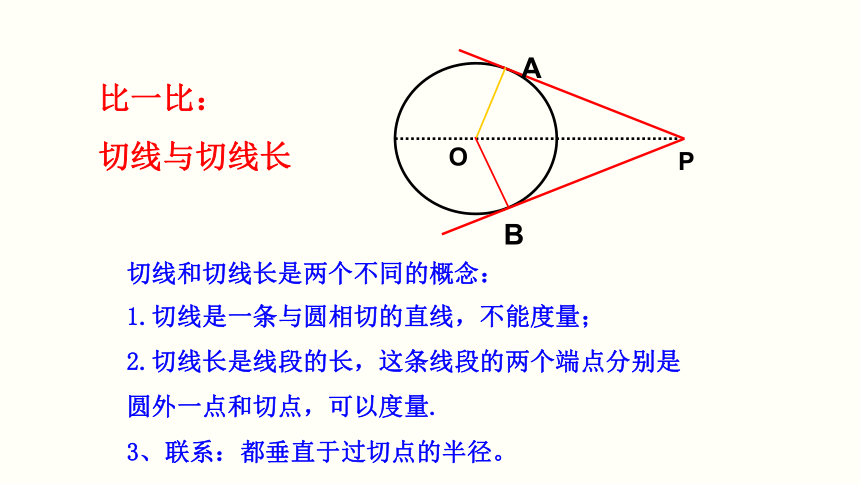
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
3、联系:都垂直于过切点的半径。
O
P
A
B
比一比:
切线与切线长
O
A
B
P
1
2
思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?
折一折
思考:请证明你所发现的结论:PA=PB,∠APO=∠BPO
O.
P
已知,如图PA、PB是☉O的两条切线,A、B为切点.
求证:PA=PB,∠APO=∠BPO.
证明:∵PA切☉O于点A,
∴ OA⊥PA.
同理可得OB⊥PB.
∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP,
∴PA=PB,∠APO=∠BPO.
推理验证
A
B
B
P
O
A
切线长定理:
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
知识要点
想一想:若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
OP垂直平分AB.
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ,∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB.
O.
P
A
B
M
想一想:若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.
证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
∴PC=PC.
∴ △PCA ≌ △PCB,
∴AC=BC.
CA=CB
O.
P
A
B
C
典例精析
例1 已知:如图,四边形ABCD的边AB、BC、CD、
DA与⊙O分别相切与点E、F、G、H.
求证:AB+CD=AD+BC.
·
A
B
C
D
O
证明:∵AB、BC、CD、DA与⊙O分别相切与点E、F、G、H,
E
F
G
H
∴ AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH.
∴AB+CD=AD+BC.
A
1.如图,PA、PB是☉O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
B
P
O
A
第1题
B
C
O
第2题
20 °
4
课堂练习
2.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45°
C.60° D.70°
D
3.如图,AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长.(结果保留根号)
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
课堂小结
如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
拓展提升
第4课时 切线长定理与
三角形的内切圆
复习回顾
3.如图:在⊙O中,OA、OB为半径,直线MN与
⊙O相切于点B,若∠ABN=30°,则∠AOB= .
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
60°
预习检测
1、切线长定理:1、过圆外一点所画的圆的两条切线,它们的切线长 .
2、这一点和圆心的连线 这两条切线的夹角。
相等
平分
3、如图,PA,PB是⊙ O的切线,切点分别是A,B,如果∠P=60°,那么∠AOB等于( )
A.60° B.90°
C.120° D.150°
C
情境导入
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
B
A
大家知道,过圆上一点可以作圆的切线有且只有一条.借助三角板,我们可以画出PA是⊙O的切线.
思考:那么,过圆外一点P能作圆的几条切线呢?
O
P
切线长定理及应用
一
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
知识要点
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
3、联系:都垂直于过切点的半径。
O
P
A
B
比一比:
切线与切线长
O
A
B
P
1
2
思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?
折一折
思考:请证明你所发现的结论:PA=PB,∠APO=∠BPO
O.
P
已知,如图PA、PB是☉O的两条切线,A、B为切点.
求证:PA=PB,∠APO=∠BPO.
证明:∵PA切☉O于点A,
∴ OA⊥PA.
同理可得OB⊥PB.
∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP,
∴PA=PB,∠APO=∠BPO.
推理验证
A
B
B
P
O
A
切线长定理:
过圆外一点作圆的两条切线,两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
知识要点
想一想:若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
OP垂直平分AB.
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ,∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB.
O.
P
A
B
M
想一想:若延长PO交⊙O于点C,连结CA、CB,你又能得出什么新的结论?并给出证明.
证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
∴PC=PC.
∴ △PCA ≌ △PCB,
∴AC=BC.
CA=CB
O.
P
A
B
C
典例精析
例1 已知:如图,四边形ABCD的边AB、BC、CD、
DA与⊙O分别相切与点E、F、G、H.
求证:AB+CD=AD+BC.
·
A
B
C
D
O
证明:∵AB、BC、CD、DA与⊙O分别相切与点E、F、G、H,
E
F
G
H
∴ AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH.
∴AB+CD=AD+BC.
A
1.如图,PA、PB是☉O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
B
P
O
A
第1题
B
C
O
第2题
20 °
4
课堂练习
2.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45°
C.60° D.70°
D
3.如图,AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长.(结果保留根号)
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
课堂小结
如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
拓展提升
