2020--2021学年七年级数学苏科版下册第7章:平面图形的认识 (二) 综合题同步训练(三)(Word版 含解析)
文档属性
| 名称 | 2020--2021学年七年级数学苏科版下册第7章:平面图形的认识 (二) 综合题同步训练(三)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 15:52:09 | ||
图片预览

文档简介
2020--2021学年七年级数学下册第7章:平面图形的认识
(二)
同步训练(三)
1.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)判断∠ADE与∠EFC是否相等,并说明理由;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
2.数学概念
百度百科这样定义凹四边形:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.
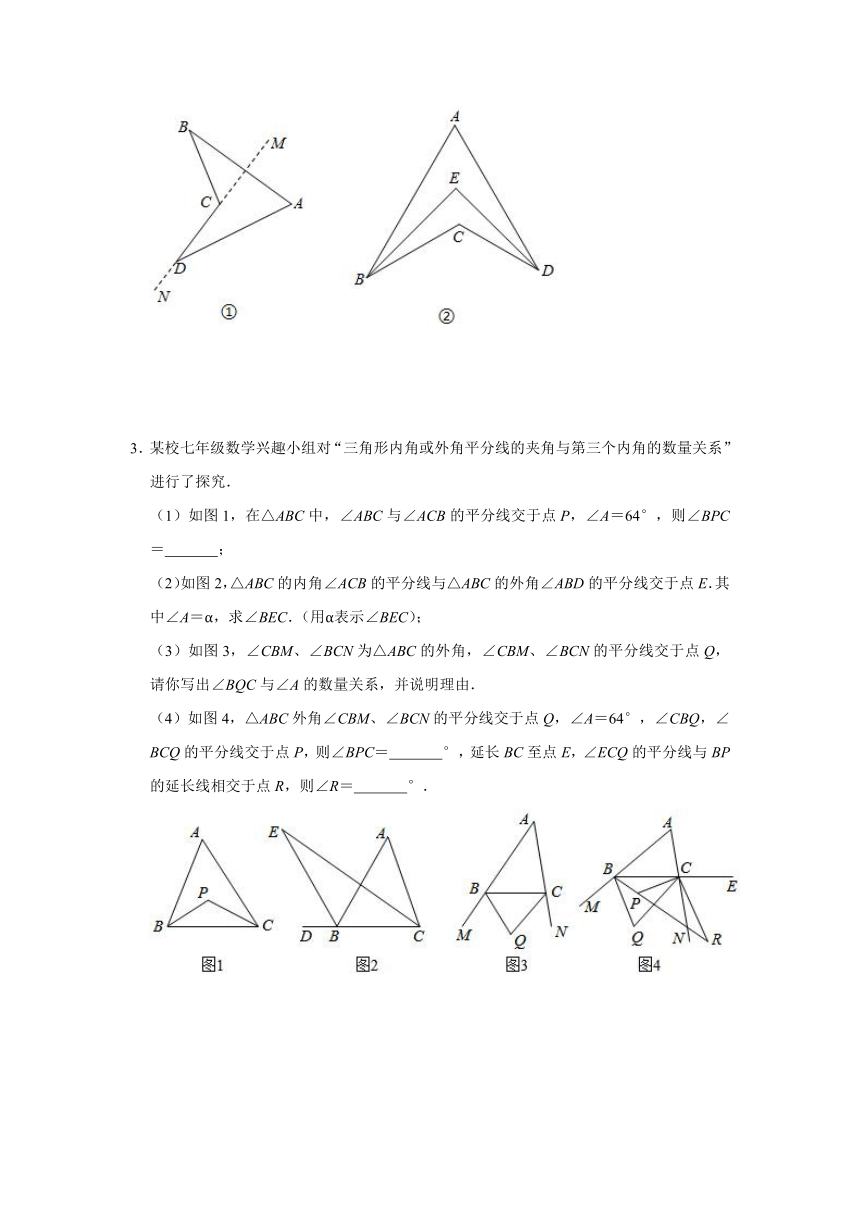
如图①,在四边形ABCD中,画出DC所在直线MN,边BC、AD分别在直线MN的两旁,则四边形ABCD就是凹四边形.
性质初探
(1)在图①所示的凹四边形ABCD中,求证:∠BCD=∠A+∠B+∠D.
深入研究
(2)如图②,在凹四边形ABCD中,AB与CD所在直线垂直,AD与BC所在直线垂直,∠B、∠D的角平分线相交于点E.
①求证:∠A+∠BCD=180°;
②随着∠A的变化,∠BED的大小会发生变化吗?如果有变化,请探索∠BED与∠A的数量关系;如果没有变化,请求出∠BED的度数.
3.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
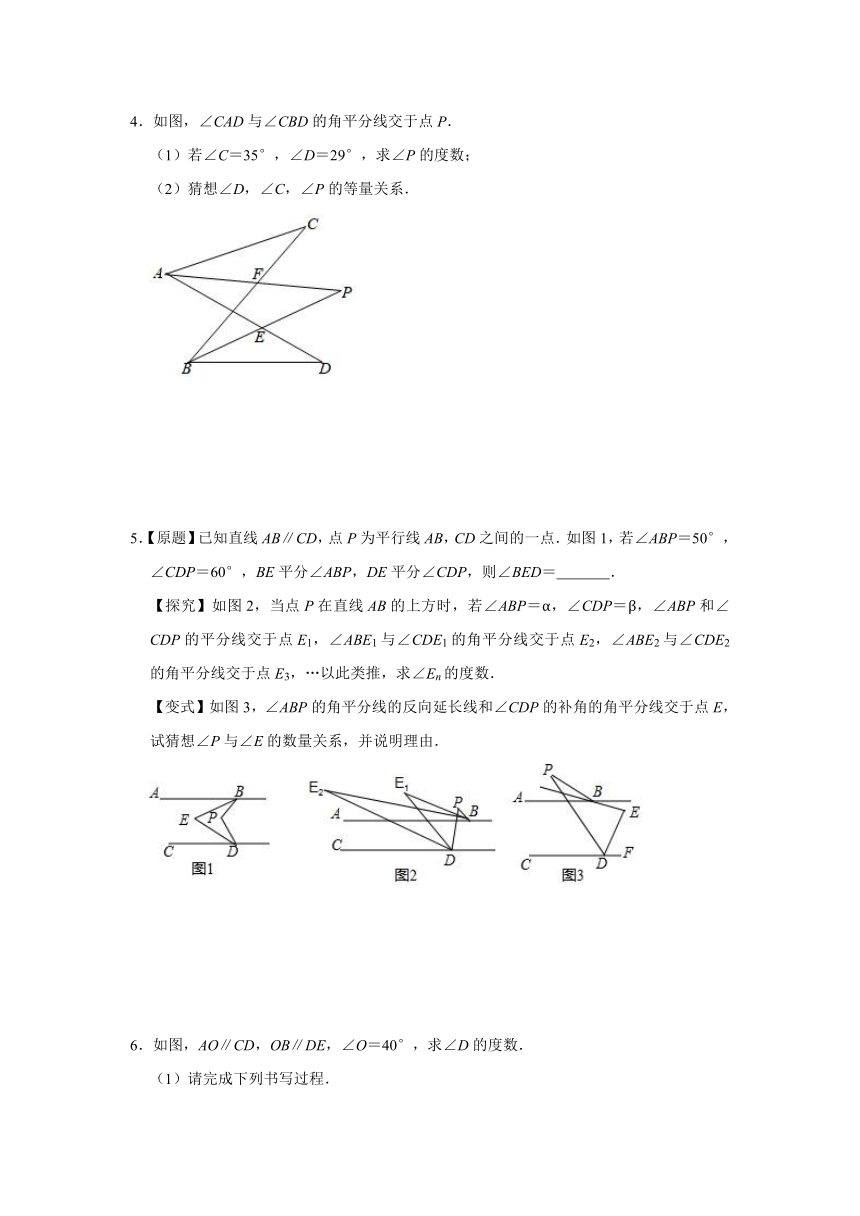
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=
;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并说明理由.
(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC=
°,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R=
°.
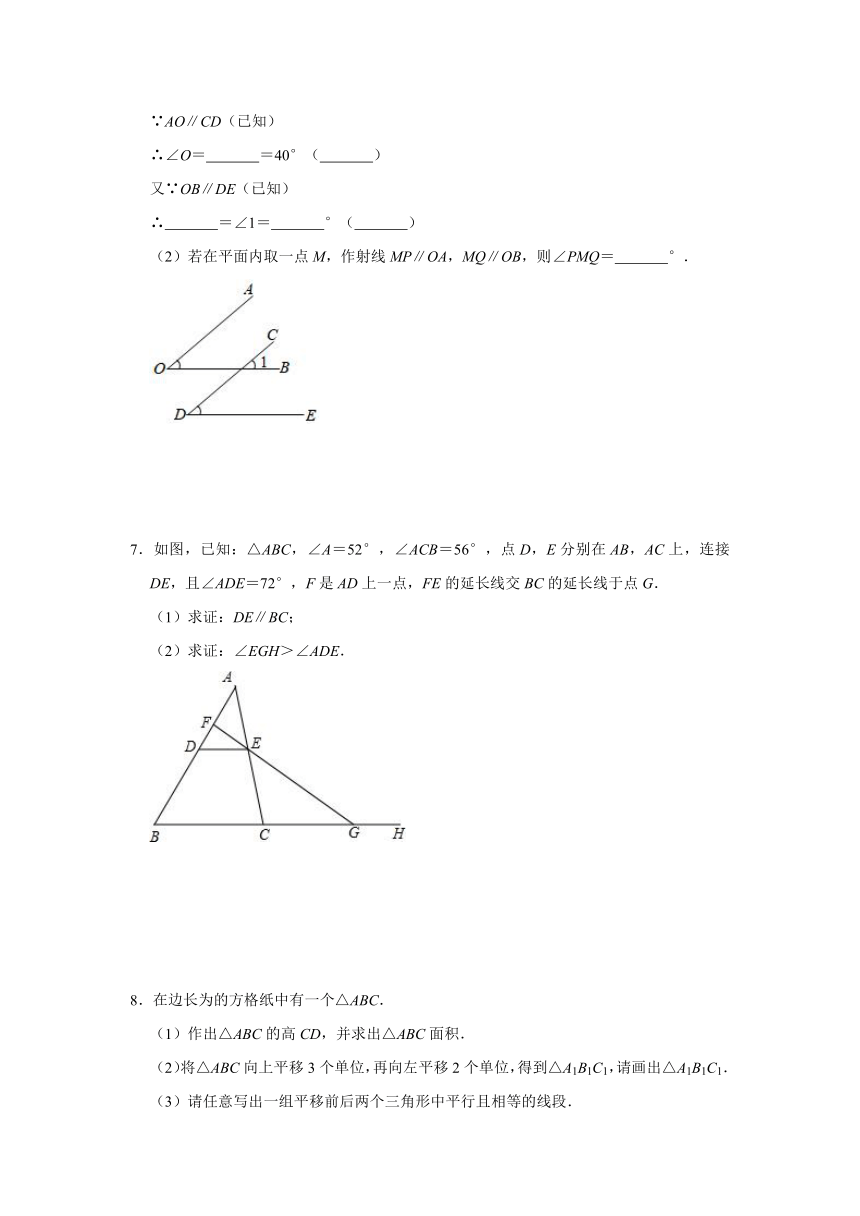
4.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
5.【原题】已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,则∠BED=
.
【探究】如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
【变式】如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
6.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
7.如图,已知:△ABC,∠A=52°,∠ACB=56°,点D,E分别在AB,AC上,连接DE,且∠ADE=72°,F是AD上一点,FE的延长线交BC的延长线于点G.
(1)求证:DE∥BC;
(2)求证:∠EGH>∠ADE.
8.在边长为的方格纸中有一个△ABC.
(1)作出△ABC的高CD,并求出△ABC面积.
(2)将△ABC向上平移3个单位,再向左平移2个单位,得到△A1B1C1,请画出△A1B1C1.
(3)请任意写出一组平移前后两个三角形中平行且相等的线段.
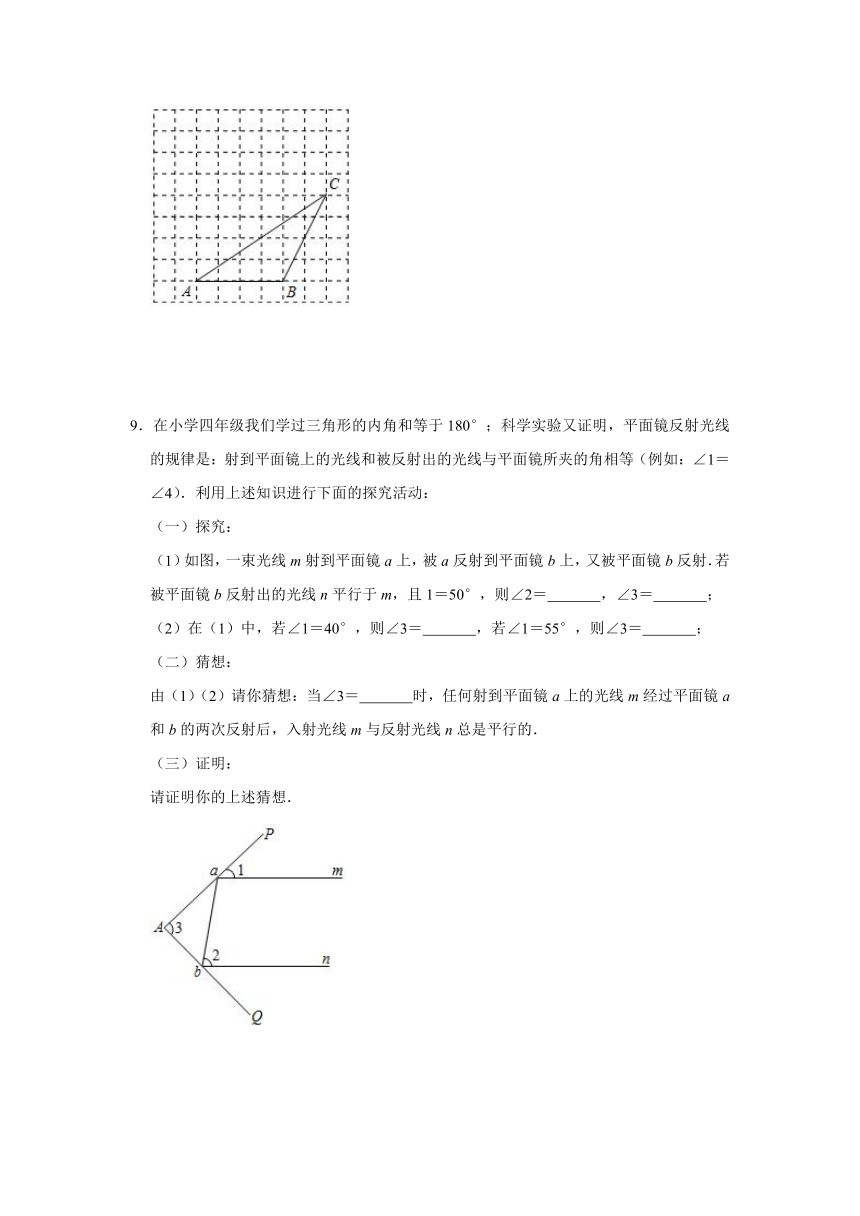
9.在小学四年级我们学过三角形的内角和等于180°;科学实验又证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等(例如:∠1=∠4).利用上述知识进行下面的探究活动:
(一)探究:
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被平面镜b反射.若被平面镜b反射出的光线n平行于m,且1=50°,则∠2=
,∠3=
;
(2)在(1)中,若∠1=40°,则∠3=
,若∠1=55°,则∠3=
;
(二)猜想:
由(1)(2)请你猜想:当∠3=
时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的.
(三)证明:
请证明你的上述猜想.
10.如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
参考答案
1.解:(1)∠ADE=∠EFC,
理由:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
2.(1)证明:如图①,延长DC交AB于点E,
∵∠BEC是△AED的一个外角,
∴∠A+∠D=∠BEC,
同理,∠B+∠BEC=∠BCD,
∴BCD=∠A+∠B+∠D.
(2)①证明:如图②,延长BC、DC分别交AD、BC于点F、G,
由题意可知,∠AFC=∠AGC=90°,
∵在四边形AFCG中,∠AFC+∠AGC+∠A+∠FCG=360°,
∴∠A+∠FCG=180°,
∵∠FCG=∠BCD,
∴∠A+∠BCD=180°;
②解:由(1)可知,在凹四边形ABED中,
∠A+∠ABE+∠ADE=∠BED①,
同理,在凹四边形EBCD中,
∠BED+∠EBC+∠EDC=∠BCD②,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
同理,∠ADE=∠EDC,
①﹣②得∠A+∠BCD=2∠BED,
由(2)①可知,在凹四边形ABCD中,∠A+∠BCD=180°,
∴2∠BED=180°,
∴∠BED=90°.
3.解:(1)∵PB、PC分别平分∠ABC和∠ACB,
∴∠PBC=ABC,∠PCB=∠ACB(角平分线的定义),
∵∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=180°﹣90°+∠A
=90°+∠A
=90
=122°.
故答案为:122°;
(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,
∴∠ECB=∠ACB,∠EBD=∠ABD.
∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,
∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,
∴∠EBD=∠ABD=(∠A+∠ACB)=∠BEC+∠ECB,即∠A+∠ECB=∠ECB+∠BEC,
∴∠BEC=∠A=;
(3)结论:∠BQC=90°﹣∠A.
理由如下:∵∠CBM与∠BCN是△ABC的外角,
∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,
∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,
∴∠QBC=(∠A+∠ACB),∠QCB=(∠A+∠ABC).
∵∠QBC+∠QCB+∠BQC=180°,
∴∠BQC=180°﹣∠QBC﹣∠QCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
=180°﹣∠A﹣90°
=90°﹣∠A;
(4)由(3)可知,∠BQC=90°﹣∠A=90°﹣=58°,
由(1)可知∠BPC=90°+∠BQC=90°+=119°;
由(2)可知,∠R=∠BQC=29°
故答案为119,29.
4.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
5.解:(1)如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=∠ABP=25°,∠CDE=∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为:55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1,
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=,
∵AB∥CD,
∴∠CDF=∠AFE1=,
∴∠E1=∠AFE1﹣∠ABE1=﹣α=(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2,
∴∠ABE2=∠ABE1=α,∠CDE2=∠CDE1=,
∵AB∥CD,
∴∠CDG=∠AGE2=,
∴∠E2=∠AGE2﹣∠ABE2=(β﹣α),
同理可得,∠E3=(β﹣α),
以此类推,∠En的度数为(β﹣α).
(3)∠DEB=90°﹣∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=∠PDF=(180°﹣∠CDP),∠ABQ=∠ABP,
∴∠DEB=∠ABP+(180°﹣∠CDP)=90°﹣(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣(∠CDP﹣∠ABP)=90°﹣(∠AHP﹣∠ABP)=90°﹣∠P.
6.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
7.(1)证明:∵∠A=52°,∠ACB=56°,
∴∠B=180°﹣∠A﹣∠ACB=72°,
∵∠ADE=72°,
∴∠B=∠ADE,
∴DE∥BC;
(2)证明:∵∠EGH是△FBG的外角,
∴∠EGH>∠B,
又∵DE∥BC,
∴∠B=∠ADE.
∴∠EGH>∠ADE.
8.解:(1)高CD如图所示,.
(2)先将点A,B,C分别向上平移3个单位,再向左平移2个单位确定点A1,B1,C1,再连接A1B1,B1C1,A1C1,此时△A1B1C1即为所求.
(3)AB与A1B1相等且平行,BC与B1C1相等且平行,AC与A1C1相等且平行,三组线段任写一组.
9.解:(一)探究:(1)如图,
∵射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,∠1=50°,
∴∠4=∠1=50°,∠5=∠7,
∴∠6=180°﹣50°﹣50°=80°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=100°,
∴∠5=∠7=40°,
∴∠3=180°﹣50°﹣40°=90°,
故答案为:100°,90°;
(2)∵∠1=40°,射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,
∴∠4=∠1=40°,∠5=∠7,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°﹣50°﹣40°=90°;
∵∠1=55°,
∴∠4=∠1=55°,
∴∠6=180°﹣55°﹣55°=70°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=110°,
∵射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,
∴∠5=∠7=35°,
∴∠3=180°﹣55°﹣35°=90°;
故答案为:90°,90°;
(二)猜想:当∠3=90°时,m∥n,
故答案为:90°;
(三)证明:∵∠3=90°,
∴∠4+∠5=180°﹣90°=90°,
∵∠1=∠4,∠7=∠5,
∴∠1+∠4+∠5+∠7=2×90°=180°,
∴∠6+∠2=180°﹣(∠1+∠4)+180°﹣(∠5+∠7)=180°,
∴m∥n.
10.证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
(二)
同步训练(三)
1.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)判断∠ADE与∠EFC是否相等,并说明理由;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
2.数学概念
百度百科这样定义凹四边形:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.
如图①,在四边形ABCD中,画出DC所在直线MN,边BC、AD分别在直线MN的两旁,则四边形ABCD就是凹四边形.
性质初探
(1)在图①所示的凹四边形ABCD中,求证:∠BCD=∠A+∠B+∠D.
深入研究
(2)如图②,在凹四边形ABCD中,AB与CD所在直线垂直,AD与BC所在直线垂直,∠B、∠D的角平分线相交于点E.
①求证:∠A+∠BCD=180°;
②随着∠A的变化,∠BED的大小会发生变化吗?如果有变化,请探索∠BED与∠A的数量关系;如果没有变化,请求出∠BED的度数.
3.某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=
;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并说明理由.
(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC=
°,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R=
°.
4.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
5.【原题】已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,则∠BED=
.
【探究】如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
【变式】如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.
6.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
7.如图,已知:△ABC,∠A=52°,∠ACB=56°,点D,E分别在AB,AC上,连接DE,且∠ADE=72°,F是AD上一点,FE的延长线交BC的延长线于点G.
(1)求证:DE∥BC;
(2)求证:∠EGH>∠ADE.
8.在边长为的方格纸中有一个△ABC.
(1)作出△ABC的高CD,并求出△ABC面积.
(2)将△ABC向上平移3个单位,再向左平移2个单位,得到△A1B1C1,请画出△A1B1C1.
(3)请任意写出一组平移前后两个三角形中平行且相等的线段.
9.在小学四年级我们学过三角形的内角和等于180°;科学实验又证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等(例如:∠1=∠4).利用上述知识进行下面的探究活动:
(一)探究:
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被平面镜b反射.若被平面镜b反射出的光线n平行于m,且1=50°,则∠2=
,∠3=
;
(2)在(1)中,若∠1=40°,则∠3=
,若∠1=55°,则∠3=
;
(二)猜想:
由(1)(2)请你猜想:当∠3=
时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的.
(三)证明:
请证明你的上述猜想.
10.如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
参考答案
1.解:(1)∠ADE=∠EFC,
理由:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
2.(1)证明:如图①,延长DC交AB于点E,
∵∠BEC是△AED的一个外角,
∴∠A+∠D=∠BEC,
同理,∠B+∠BEC=∠BCD,
∴BCD=∠A+∠B+∠D.
(2)①证明:如图②,延长BC、DC分别交AD、BC于点F、G,
由题意可知,∠AFC=∠AGC=90°,
∵在四边形AFCG中,∠AFC+∠AGC+∠A+∠FCG=360°,
∴∠A+∠FCG=180°,
∵∠FCG=∠BCD,
∴∠A+∠BCD=180°;
②解:由(1)可知,在凹四边形ABED中,
∠A+∠ABE+∠ADE=∠BED①,
同理,在凹四边形EBCD中,
∠BED+∠EBC+∠EDC=∠BCD②,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
同理,∠ADE=∠EDC,
①﹣②得∠A+∠BCD=2∠BED,
由(2)①可知,在凹四边形ABCD中,∠A+∠BCD=180°,
∴2∠BED=180°,
∴∠BED=90°.
3.解:(1)∵PB、PC分别平分∠ABC和∠ACB,
∴∠PBC=ABC,∠PCB=∠ACB(角平分线的定义),
∵∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=180°﹣90°+∠A
=90°+∠A
=90
=122°.
故答案为:122°;
(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,
∴∠ECB=∠ACB,∠EBD=∠ABD.
∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,
∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,
∴∠EBD=∠ABD=(∠A+∠ACB)=∠BEC+∠ECB,即∠A+∠ECB=∠ECB+∠BEC,
∴∠BEC=∠A=;
(3)结论:∠BQC=90°﹣∠A.
理由如下:∵∠CBM与∠BCN是△ABC的外角,
∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,
∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,
∴∠QBC=(∠A+∠ACB),∠QCB=(∠A+∠ABC).
∵∠QBC+∠QCB+∠BQC=180°,
∴∠BQC=180°﹣∠QBC﹣∠QCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
=180°﹣∠A﹣90°
=90°﹣∠A;
(4)由(3)可知,∠BQC=90°﹣∠A=90°﹣=58°,
由(1)可知∠BPC=90°+∠BQC=90°+=119°;
由(2)可知,∠R=∠BQC=29°
故答案为119,29.
4.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
5.解:(1)如图1,过E作EF∥AB,而AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠FEB,∠CDE=∠FED,
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,
又∵∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,
∴∠ABE=∠ABP=25°,∠CDE=∠CDP=30°,
∴∠BED=25°+30°=55°,
故答案为:55°;
(2)如图2,∵∠ABP和∠CDP的平分线交于点E1,
∴∠ABE1=∠ABP=α,∠CDE1=∠CDP=,
∵AB∥CD,
∴∠CDF=∠AFE1=,
∴∠E1=∠AFE1﹣∠ABE1=﹣α=(β﹣α),
∵∠ABE1与∠CDE1的角平分线交于点E2,
∴∠ABE2=∠ABE1=α,∠CDE2=∠CDE1=,
∵AB∥CD,
∴∠CDG=∠AGE2=,
∴∠E2=∠AGE2﹣∠ABE2=(β﹣α),
同理可得,∠E3=(β﹣α),
以此类推,∠En的度数为(β﹣α).
(3)∠DEB=90°﹣∠P.理由如下:
如图3,过E作EG∥AB,而AB∥CD,
∴AB∥CD∥EG,
∴∠MBE=∠BEG,∠FDE=∠GED,
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE,
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,
∴∠FDE=∠PDF=(180°﹣∠CDP),∠ABQ=∠ABP,
∴∠DEB=∠ABP+(180°﹣∠CDP)=90°﹣(∠CDP﹣∠ABP),
∵AB∥CD,
∴∠CDP=∠AHP,
∴∠DEB=90°﹣(∠CDP﹣∠ABP)=90°﹣(∠AHP﹣∠ABP)=90°﹣∠P.
6.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
7.(1)证明:∵∠A=52°,∠ACB=56°,
∴∠B=180°﹣∠A﹣∠ACB=72°,
∵∠ADE=72°,
∴∠B=∠ADE,
∴DE∥BC;
(2)证明:∵∠EGH是△FBG的外角,
∴∠EGH>∠B,
又∵DE∥BC,
∴∠B=∠ADE.
∴∠EGH>∠ADE.
8.解:(1)高CD如图所示,.
(2)先将点A,B,C分别向上平移3个单位,再向左平移2个单位确定点A1,B1,C1,再连接A1B1,B1C1,A1C1,此时△A1B1C1即为所求.
(3)AB与A1B1相等且平行,BC与B1C1相等且平行,AC与A1C1相等且平行,三组线段任写一组.
9.解:(一)探究:(1)如图,
∵射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,∠1=50°,
∴∠4=∠1=50°,∠5=∠7,
∴∠6=180°﹣50°﹣50°=80°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=100°,
∴∠5=∠7=40°,
∴∠3=180°﹣50°﹣40°=90°,
故答案为:100°,90°;
(2)∵∠1=40°,射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,
∴∠4=∠1=40°,∠5=∠7,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°﹣50°﹣40°=90°;
∵∠1=55°,
∴∠4=∠1=55°,
∴∠6=180°﹣55°﹣55°=70°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=110°,
∵射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等,
∴∠5=∠7=35°,
∴∠3=180°﹣55°﹣35°=90°;
故答案为:90°,90°;
(二)猜想:当∠3=90°时,m∥n,
故答案为:90°;
(三)证明:∵∠3=90°,
∴∠4+∠5=180°﹣90°=90°,
∵∠1=∠4,∠7=∠5,
∴∠1+∠4+∠5+∠7=2×90°=180°,
∴∠6+∠2=180°﹣(∠1+∠4)+180°﹣(∠5+∠7)=180°,
∴m∥n.
10.证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
