2020-2021学年下学期华东师大版八年级数学下册 18.2 平行四边形的判定(培优卷)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年下学期华东师大版八年级数学下册 18.2 平行四边形的判定(培优卷)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 350.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览


文档简介
117221001131570018.2 平行四边形的判定(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD B.OA=OC,AB∥CD
C.AB=CD,OA=OC D.∠ADB=∠CBD,∠BAD=∠BCD
2.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.88°,108°,88° B.88°,104°,108° C.88°,92°,92° D.88°,92°,88°
3.下列说法错误的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4 B.1:4:2:3 C.1:2:2:1 D.1:2:1:2
5.如图所示,在四边形
中, ,要使四边形成为平行四边形还需要条件( )
A. B. C. D.
6.如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
7.如图,设是平行四边形ABCD边上任意一点,设△AMD的面积为,△BMC的面积为,△CDM的面积为,则( )
A. B. C. D.不能确定
8.如图,E,F分别是 平行四边形ABCD的边AB,CD的中点,则图中平行四边形的个数共有( ).
A.2个 B.3个 C.4个 D.5个
9.如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
A.8 B.12 C.16 D.32
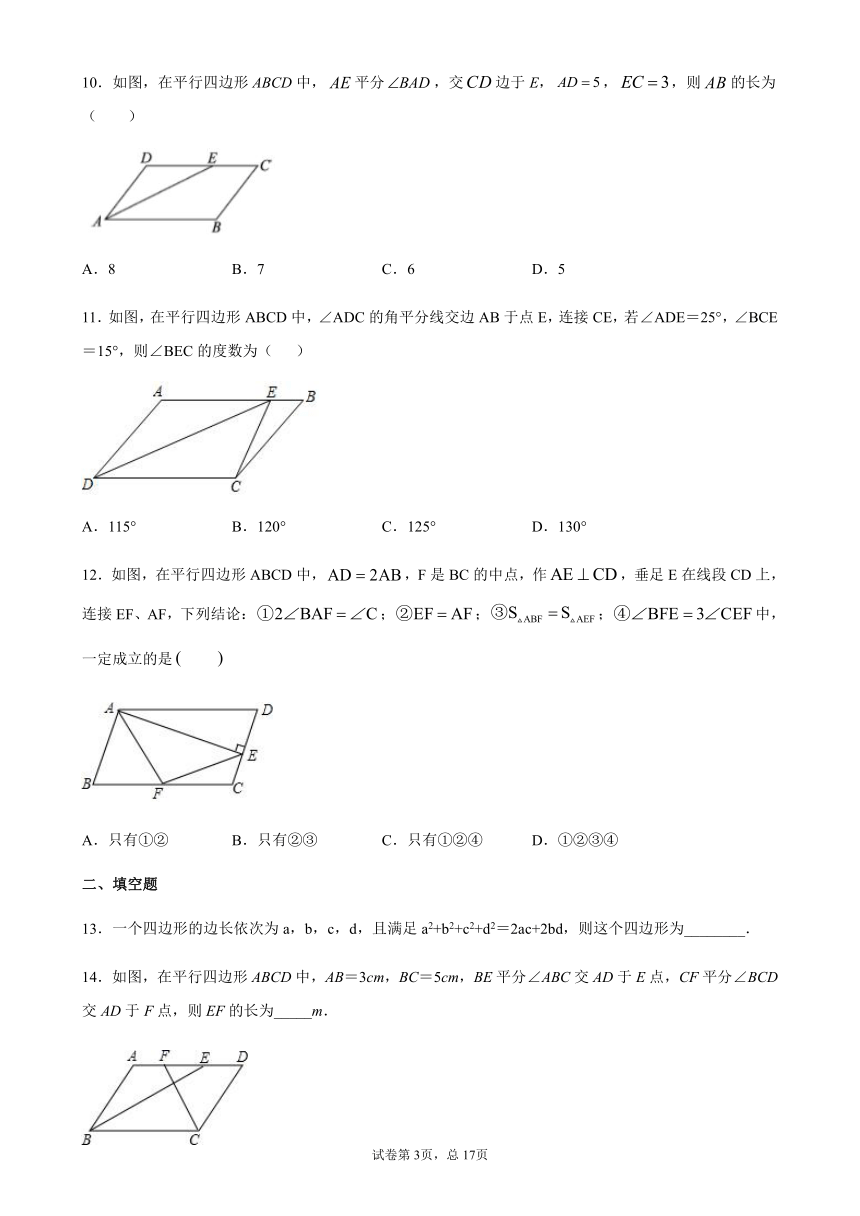
10.如图,在平行四边形ABCD中,平分,交边于E,,,则的长为( )
A.8 B.7 C.6 D.5
11.如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A.115° B.120° C.125° D.130°
12.如图,在平行四边形ABCD中,,F是BC的中点,作,垂足E在线段CD上,连接EF、AF,下列结论:;;;中,一定成立的是
A.只有①② B.只有②③ C.只有①②④ D.①②③④
二、填空题
13.一个四边形的边长依次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为________.
14.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E点,CF平分∠BCD交AD于F点,则EF的长为_____m.
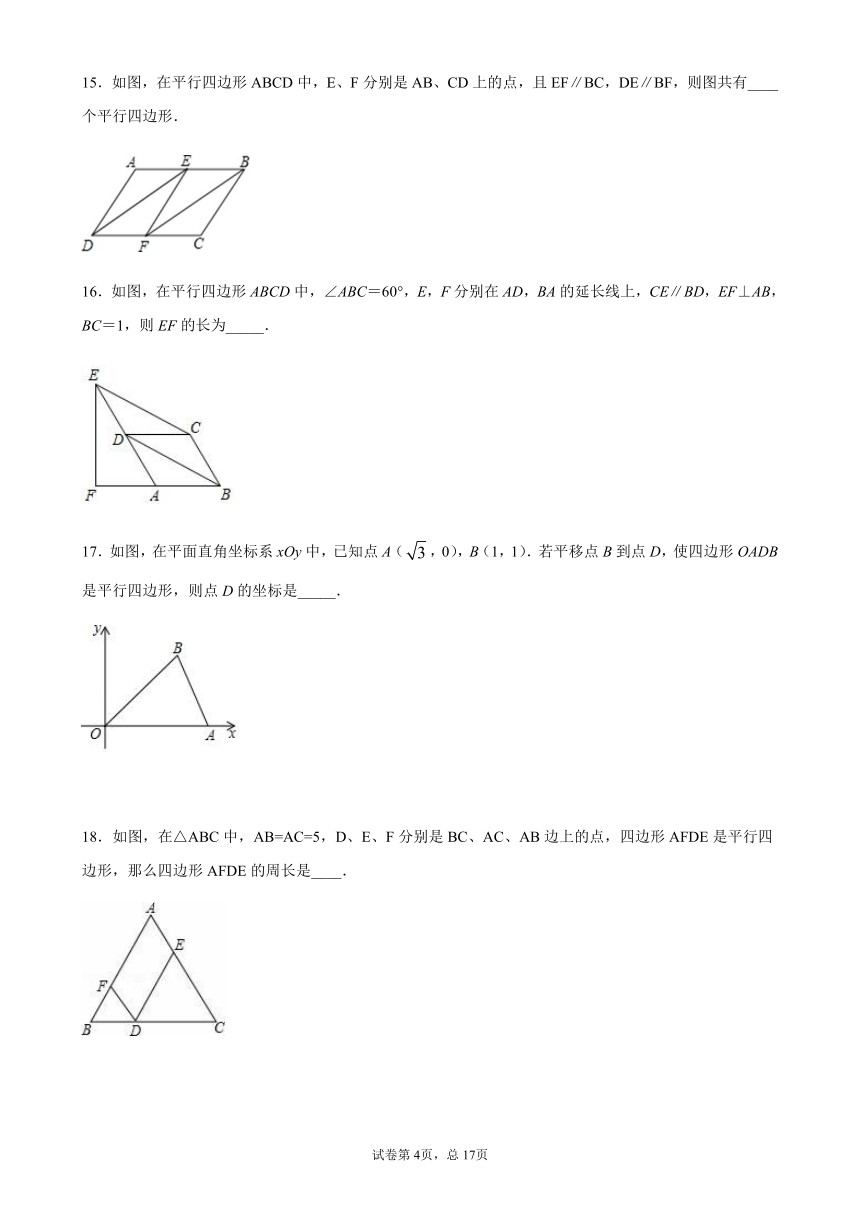
15.如图,在平行四边形ABCD中,E、F分别是AB、CD上的点,且EF∥BC,DE∥BF,则图共有____个平行四边形.
16.如图,在平行四边形ABCD中,∠ABC=60°,E,F分别在AD,BA的延长线上,CE∥BD,EF⊥AB,BC=1,则EF的长为_____.
17.如图,在平面直角坐标系xOy中,已知点A(,0),B(1,1).若平移点B到点D,使四边形OADB是平行四边形,则点D的坐标是_____.
18.如图,在△ABC中,AB=AC=5,D、E、F分别是BC、AC、AB边上的点,四边形AFDE是平行四边形,那么四边形AFDE的周长是____.
三、解答题
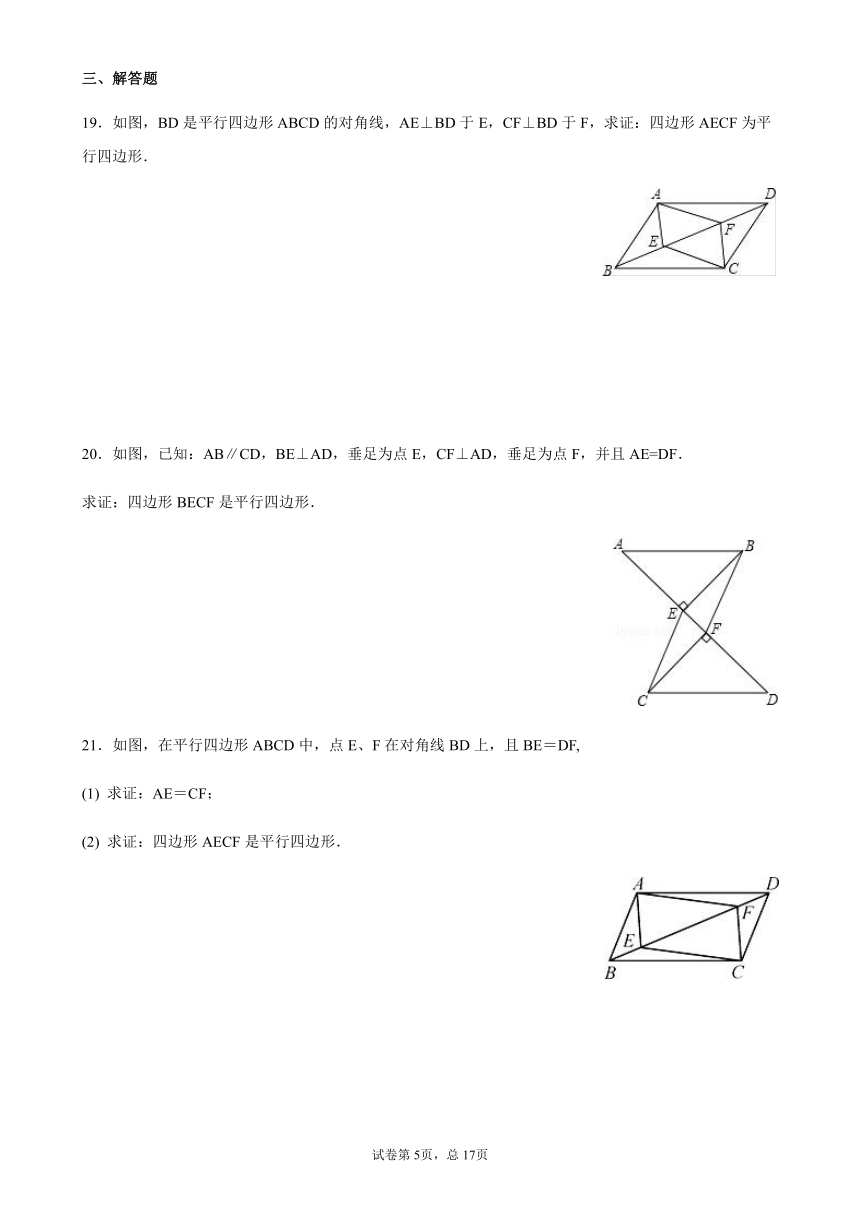
19.如图,BD是平行四边形ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
20.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
21.如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF,
(1) 求证:AE=CF;
(2) 求证:四边形AECF是平行四边形.
22.在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1) 如图1,当点E恰好在AC上时,求∠CDE的度数;
(2) 如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
23.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC ≌ △DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
24.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
25.如图,在平行四边形ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
26.如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
D
C
D
B
B
A
C
C
A
A
C
二、填空题
13
14
15
16
17
18
平行四边形
1
3
(,1)
10
三、解答题
19. ∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠ABE=∠CDF,
∵ AE⊥BD,CF⊥BD,
∴ ∠AEB=∠CFD=90°,AE∥CF,
在△AEB和△CFD中,
∵ ,
∴ △AEB≌△CFD(AAS),
∴ AE=CF,
∵ AE∥CF,
∴ 四边形AECF是平行四边形.
20. 证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
21. (1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
22. 解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180°?30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75°?60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
23. 证明:(1)∵ BE=FC
∴ BC=FE
在△ABC和△DFE中,
∵ ,
∴ △ABC≌ △DFE(SSS)
(2)解:如图所示:
由知△ABC≌ △DFE,
∴ ∠ABC=∠DFE
∴ AB//DF
∵ AB=DF
∴ 四边形ABDF是平行四边形.??
24. 证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE﹣∠ACE=∠ACF﹣∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
25. 解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN===13.
26. (1)解:∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB=BC,
∵△ABD和△ACE均为等腰直角三角形,
∴BD===2BC,
∵G为BD的中点,
∴BG=BD=BC,
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,
∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
,
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
,
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD B.OA=OC,AB∥CD
C.AB=CD,OA=OC D.∠ADB=∠CBD,∠BAD=∠BCD
2.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.88°,108°,88° B.88°,104°,108° C.88°,92°,92° D.88°,92°,88°
3.下列说法错误的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4 B.1:4:2:3 C.1:2:2:1 D.1:2:1:2
5.如图所示,在四边形
中, ,要使四边形成为平行四边形还需要条件( )
A. B. C. D.
6.如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
7.如图,设是平行四边形ABCD边上任意一点,设△AMD的面积为,△BMC的面积为,△CDM的面积为,则( )
A. B. C. D.不能确定
8.如图,E,F分别是 平行四边形ABCD的边AB,CD的中点,则图中平行四边形的个数共有( ).
A.2个 B.3个 C.4个 D.5个
9.如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
A.8 B.12 C.16 D.32
10.如图,在平行四边形ABCD中,平分,交边于E,,,则的长为( )
A.8 B.7 C.6 D.5
11.如图,在平行四边形ABCD中,∠ADC的角平分线交边AB于点E,连接CE,若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A.115° B.120° C.125° D.130°
12.如图,在平行四边形ABCD中,,F是BC的中点,作,垂足E在线段CD上,连接EF、AF,下列结论:;;;中,一定成立的是
A.只有①② B.只有②③ C.只有①②④ D.①②③④
二、填空题
13.一个四边形的边长依次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为________.
14.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E点,CF平分∠BCD交AD于F点,则EF的长为_____m.
15.如图,在平行四边形ABCD中,E、F分别是AB、CD上的点,且EF∥BC,DE∥BF,则图共有____个平行四边形.
16.如图,在平行四边形ABCD中,∠ABC=60°,E,F分别在AD,BA的延长线上,CE∥BD,EF⊥AB,BC=1,则EF的长为_____.
17.如图,在平面直角坐标系xOy中,已知点A(,0),B(1,1).若平移点B到点D,使四边形OADB是平行四边形,则点D的坐标是_____.
18.如图,在△ABC中,AB=AC=5,D、E、F分别是BC、AC、AB边上的点,四边形AFDE是平行四边形,那么四边形AFDE的周长是____.
三、解答题
19.如图,BD是平行四边形ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
20.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
21.如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF,
(1) 求证:AE=CF;
(2) 求证:四边形AECF是平行四边形.
22.在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1) 如图1,当点E恰好在AC上时,求∠CDE的度数;
(2) 如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
23.如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)求证:△ABC ≌ △DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
24.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
25.如图,在平行四边形ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
26.如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
D
C
D
B
B
A
C
C
A
A
C
二、填空题
13
14
15
16
17
18
平行四边形
1
3
(,1)
10
三、解答题
19. ∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠ABE=∠CDF,
∵ AE⊥BD,CF⊥BD,
∴ ∠AEB=∠CFD=90°,AE∥CF,
在△AEB和△CFD中,
∵ ,
∴ △AEB≌△CFD(AAS),
∴ AE=CF,
∵ AE∥CF,
∴ 四边形AECF是平行四边形.
20. 证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
21. (1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
22. 解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180°?30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75°?60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
23. 证明:(1)∵ BE=FC
∴ BC=FE
在△ABC和△DFE中,
∵ ,
∴ △ABC≌ △DFE(SSS)
(2)解:如图所示:
由知△ABC≌ △DFE,
∴ ∠ABC=∠DFE
∴ AB//DF
∵ AB=DF
∴ 四边形ABDF是平行四边形.??
24. 证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE﹣∠ACE=∠ACF﹣∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
25. 解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN===13.
26. (1)解:∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB=BC,
∵△ABD和△ACE均为等腰直角三角形,
∴BD===2BC,
∵G为BD的中点,
∴BG=BD=BC,
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,
∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
,
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
,
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.
