中考数学复习专题——直角三角形常考的10个易错点浅析学案(附答案)
文档属性
| 名称 | 中考数学复习专题——直角三角形常考的10个易错点浅析学案(附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 21:09:22 | ||
图片预览




文档简介
1203960012268200直角三角形常考的10个易错点浅析
直角三角形的性质
性质1:直角三角形两锐角互余.
性质2:直角三角形斜边上的中线等于斜边的一半.
性质3:直角三角形中30o所对的直角边等于斜边的一半.
直角三角形的判定
判定1:有两个角互余的三角形是直角三角形.
判定2:一边上的中线等于这边的一半的三角形是直角三角形.
直角三角形的性质
勾股定理:如果直角三角形的两直角边为a 和b ,斜边为 c ,那么false.
直角三角形的判定
勾股定理逆定理:如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
直角三角形全等的判断:
斜边和一直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边公理”或“HL”)
角平分线的性质定理:
角平分线上的点到角的两边的距离相等.
角平分线的性质定理的逆定理:
角平分线性质定理: 角平分线上的点到角的两边的距离相等.
忽略了运用直角三角形的性质的前提条件
在运用直角三角形的性质时,它的前提是在直角三角形中.如果三角形不是直角三角形,那么这些性质就不存在了,所以运用时要注意前提条件。
如图,在△ABC中,CD是AB边上的高,∠A=60°,则∠BCD的度数为( )
A.30° B.60° C.90° D.无法确定
【错解】B
【错因】在本题中没有指明△ABC是直角三角形,故不能利用直角三角形的性质进行计算。错解中想当然地认为△ABC是直角三角形,然后利用了直角三角形的性质,进而造成错解。
【正解】D
如图,在△ABC中,∠ABC=75°,从顶点B引射线BD与CA交于D点,使∠CDB=30°,BD=AD。求证:AD=2BC。
【错解】在△BCD中,∵∠CDB=30°,∴BC=12BD。∵BD=AD,∴BC=12AD,即AD=2BC
【错因】在本题中没有指明∠C=90O,故不能直接利用直角三角形的性质进行计算。在本题中应该先利用已知条件证出∠C=90O,再利用直角三角形的性质证明BD=2BC,进而得出AD=2BC
【正解】∵∠CDB=30°,BD=AD,∴∠A=∠ABD=12∠CDB=15°
∵∠ABC=75°,∴∠A+∠ABC=90°,∴∠C=90°
在Rt△BCD中,∵∠CDB=30°,∴BC=12BD
∵BD=AD ,∴BC=12AD,即AD=2BC。
在△ABC中,CD是AB边上的中线,若AB=6,则CD的长是( )
A.2 B.3 C.6 D.无法确定
【错解】B
【正解】D
【小结】“直角三角形两锐角互余”、“直角三角形斜边上的中线等于斜边的一半”、“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”这三个定理是直角三角形特有的性质时,所以在运用这几个性质时一定要注意前提条件是“在直角三角形中”。
误用直角三角形的性质
如图,在△ABC中,∠ACB=90°,BD=CD。求证:CD=AD。
【错解】在△ABC中,∵∠ACB=90°,
∴BD=CD,
∴CD=12AB=AD,
【错因】在本题已知条件中没有告诉点D为直角三角形斜边上的中点,故不能利用直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”来证明。
【正解】∵BD=CD,
∴∠BCD=∠B
∵∠ACB=90°,
∴∠BCD+∠ACD=90°,∠B+∠A=90°
∴∠ACD=∠A,
∴CD=AD
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,∠ABC的平分线为BD,且AD的长为15cm,求AC的长
【错解】在Rt△ABC中,∵∠C=90°,∠ABC=60°,BD平分∠A BC
∴∠A=30°,∠CBD=12∠ABC=30°
∴AC=2BC,BC=2CD,
∴AC=4CD,即CD=14AC
又∵AD+CD=AC 且 AD=15cm,∴AC=20cm
【正解】在Rt△ABC中,∵∠C=90°,∠ABC=60°,BD平分∠ABC
∴∠A=30°,∠CBD=∠ABD=12∠ABC=30°
∴CD =12BD, ∠A=∠ABD
∴AD=BD,∴CD=12AD
又∵AD+CD=AC且AD=15cm
∴AC=32AD= 22.5cm
【小结】运用直角三角形的性质解题时,如果审题不清或对直角三角形的性质理解不透彻的话,都会出现误用直角三角形的性质解题的现象,从而出现解题过程或解题结果出现错误。
因题目中没有图形而忽视分类讨论
对于一些求三角形(尤其是等腰三角形)的边长和角的度数的题目,当没有给出三角形的形状时,要注意分情况考虑,防止漏解.
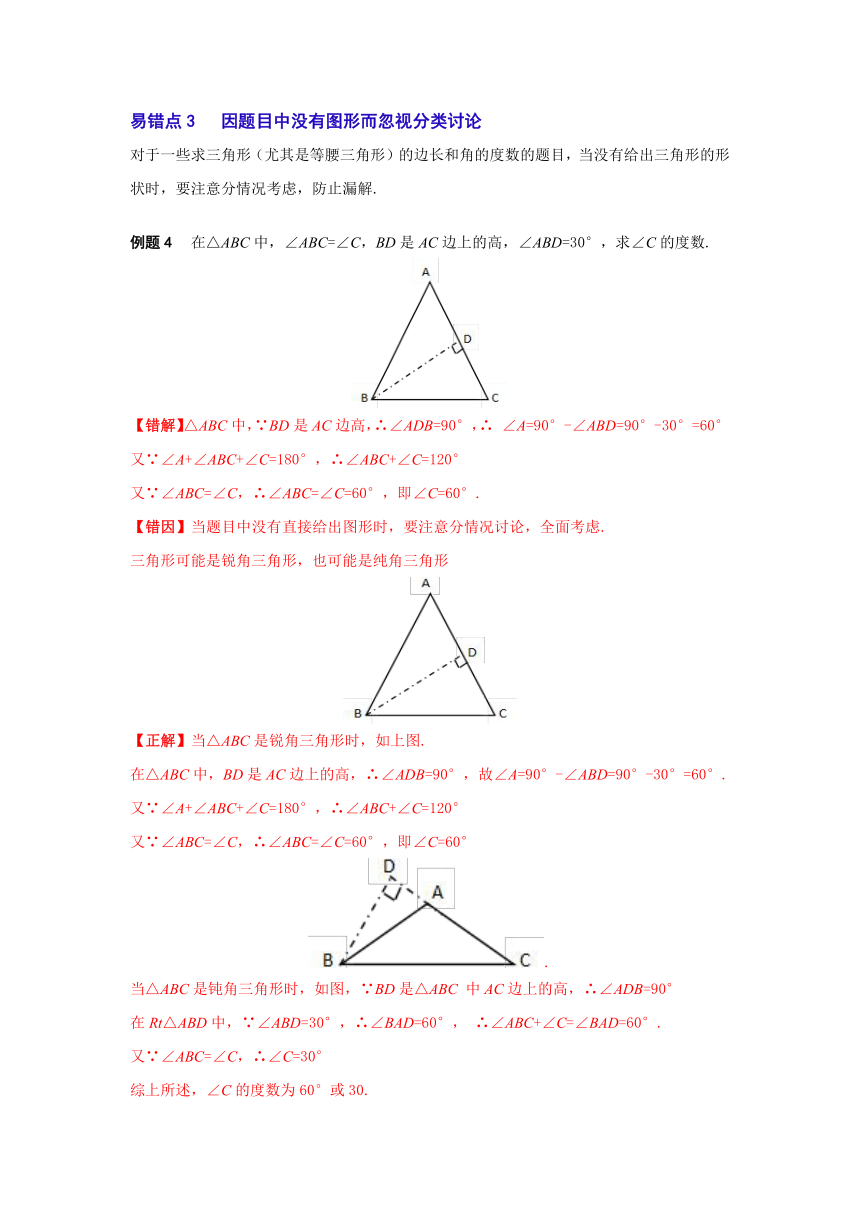
在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,求∠C的度数.
【错解】△ABC中,∵BD是AC边高,∴∠ADB=90°,∴ ∠A=90°-∠ABD=90°-30°=60°
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°
又∵∠ABC=∠C,∴∠ABC=∠C=60°,即∠C=60°.
【错因】当题目中没有直接给出图形时,要注意分情况讨论,全面考虑.
三角形可能是锐角三角形,也可能是纯角三角形
【正解】当△ABC是锐角三角形时,如上图.
在△ABC中,BD是AC边上的高,∴∠ADB=90°,故∠A=90°-∠ABD=90°-30°=60°.
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°
又∵∠ABC=∠C,∴∠ABC=∠C=60°,即∠C=60°
.
当△ABC是钝角三角形时,如图,∵BD是△ABC 中AC边上的高,∴∠ADB=90°
在Rt△ABD中,∵∠ABD=30°,∴∠BAD=60°, ∴∠ABC+∠C=∠BAD=60°.
又∵∠ABC=∠C,∴∠C=30°
综上所述,∠C的度数为60°或30.
若等腰三角形一腰上的高与腰之比为1:2,则等腰三角形顶角的度数为( )
A.30° B.60°或120° C.30°或150° D.150°
【错解】A
【正解】C
已知在等腰△ABC中,AD⊥BC,垂足为点D,且AD=falseBC,求△ABC底角的度数。
【错解】如图,∵AB=AC,AD⊥BC,∴BD=CD.
∵AD=12BC,∴AD=BD=CD。
在Rt△ABD中,∠B=∠BAD=12 (180°-90°)=45°,
在Rt△ACD中,∠C=∠C40==12 (180°-90°)=45°
【正解】如图①,当AB=AC时,
∵AB=AC,AD⊥BC,∴∠B =∠C,BD=CD.
∵AD=12BC,∴AD=BD=CD。
在Rt△ABD中,∠B=∠BAD=12 (180°-90°)=45°,
当AC=BC时,
如图②,AD在△ABC外部时,∵AD=12BC,AC= BC,
∴AD=12AC,∠BAC=∠B,∴∠ACD=30°,
∵∠BAC+∠B=∠ACD,∴∠BAC=∠B=12×30°=15°
如图③,AD在△ABC内部时,∵AD=12BC,AC= BC,
∴AD=12AC, ∠BAC=∠B,∴∠C=30°,
∴∠BAC=∠B=12×(180°-∠C)=75°
综上所述,△ABC的底角的度数为45°或15°或75°.
(思考:为什么可以不讨论AB=BC时的情形?)
【小结】由于三角形的高可能在三角形内,也可能在三角形外,还有可能与三角形的边重合,所以在求涉及三角形(尤其是等腰三角形)高的边长和角的度数的题目时,若无图形,一般要进行分类讨论。
受思维定式的影响,误认为在RtΔABC中,c总表示斜边
在△ABC中,∠A=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=6,b=8,则c= .
【错解】10
【错因】对勾股定理理解不透彻,受勾股定理即勾股数的影响,误认为在RtΔABC中,c总表示斜边,从而求得错解
【正解】false
在△ABC中,∠A+∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,则c= .
【错解】5
【正解】false
【小结】在应用定理解题时,一定要弄清直角是哪一个角,进一步区别开斜边与直角边,不要误认为只要是在RtΔABC中,总有a2+b2=c2即false。
求不能确定斜边的直角三角形的第三边漏解
在直角三角形中,若已知边没指明是直角边,还是斜边,则要分情况进行讨论。
已知直角三角形的两边长分别为3,4,求第三边的长.
【错解】∵32+42=52,∴第三边长为5
【错因】习惯了“勾三股四弦五”的说法,即两直角边长为3和4时,斜边长为5.但这一说法的前提是以3,4为直角边长。而本题中并未说明,因此所求的第三边可能为斜边,也可能为直角边。
【正解】当两直角边长分别为3和4时,第三边长为false;
当斜边长为4,一条直角边长为3时,第三边长为false.
综上所述,第三边长为5或false.
已知一直角三角形的三边长分别为5,12,x,求以x为边长.的正方形面积。
【错解】由勾股定理得:x2=52+122=25+144=169,以x为边长的正方形面积为169。
【正解】∵x可能是斜边长,也有可能是直角边长,
∴由勾股定理得:x2=52+122=25+144=169或x2=122-52=144-25=119
∴以x为边长的正方形面积为169或119。
【小结】 已知直角三角形两条边长求第三条边的长时,如果题目中没有明确直角边和斜边,在利用勾股定理时要注意分情况讨论。
忽略了勾股定理的前提
利用勾股定理的前提条件是在直角三角形中,脱离直角三角形,就无法利用勾股定理。
已知在△ABC中,三边长为偶数,若AB>BC>AC,且AB=10,BC=8.试求AC的长.
【错解】在△ABC中,AB>BC>AC,AB是斜边。由勾股定理得AB2=AC2+BC2,即false
又∵AB=10,BC=8,∴false,∴AC的长是6.
【错因】勾股定理在直角三角形中才成立.本题中并没有说明△ABC是直角三角形,所以不能利用勾股定理求解.根据题设条件可以利用三角形的三边关系求解.
【正解】在△ABC中,∵AB=10,BC=8,∴2AC,∴2而AC是偶数,∴AC的长只能取4或6.
如图,在△ABC中,AC=4,BC=3,则下列对AB的长的说法正确的是( )。
A.AB等于5 B.AB<7 C.AB>1 D.1【错解】A
【正解】D
【小结】勾股定理是用于计算直角三角形边长的,所以在运用勾股定理时,必须先判定三角形是直角三角形,不能确定是直角三角形就不能套用勾股定理。受新知识及图形影响,没有认真思考,凭直感觉错误的套用新知识解题就会出现错解
不认真斟酌凭感觉解题,导致考虑不周到而出现错解
一架5m长的梯子,斜靠在一竖直的墙上,这时梯足距墙脚1.4m,若梯子的顶端下滑0.8m,则梯足将滑动
【错解】1(m)
【错因】本题没有建立相关模型,仅仅凭感觉就得出了答案,这往往是不可靠的。要想得出真解,首先根据描述建立模型:
【正解】如图,设梯子下滑之前顶端在A点,梯足在B点,墙脚设为C点,这样组成了一个Rt△ABC。梯子下滑后,梯子顶端在A'点,梯足在B'点,仍然构成Rt△A'B'C,只要求出B'C的长即可知道梯足滑动的距离。在Rt△ABC中,∠C=90°,AB=5m,BC=1.4m。
由勾股定理得AB2=AC2+BC2,∴false(m)。
在Rt△A'B'C中,∠C=90°,A'C=AC-AA'=4.8-0.8=4(m),A'B'=5m。
由勾股定理得A'B2=A'C2+B'C2,所以false(m)。
所以BB'=B'C-BC=3-1.4=1.6(m)。
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.false B.25 C.false D.35
【错解】A或C或D
【正解】将长方体展开,前、右两个侧面展开图如右上图所示,连接A、B,根据两点之间线段最短可知,线段AB的长即为蚂蚁爬行的最短距离;此时
如图,BD=10+5=15,AD=20,由勾股定理得:false,选B
【小结】对问题思考过于简单,就会对问题考虑不全面,产生错误的解答。
没有确定最长边而造成判断三角形形状时出错
已知三角形中三边长分别为2.5,2,l.5,试判断该三角形是不是直角三角形.
【错解】∵2.52+22≠1.52
∴该三角形不是直角三角形
【错因】受思维定式的限制,误认为勾股定理中的a,b,c分别是2.5,2,1.5,没有确定三条边中的最长边,导致出错.
【正解】∵1.52+22=2.52,∴该三角形是直角三角形.
判断由线段a,b,c组成的三角形是不是直角三角形,其中a=false,b=false,c=1。
【错解】∵false,∴该三角形不是直角三角形
【正解】∵false, ∴该三角形是直角三角形
【小结】在利用勾股定理逆定理判断三角形形状时,要确定三边中最长边,再由数量关系确定位置关系.
误认为以常见勾股数的平方(或倒数或算术平方根)为长的线段也能构成直角三角形
下列几组线段:①1,false,false;②32,42,52;③false,false,false;其中可以构成直角三角形的有 (填序号)
【错解】①②③
【错因】但凡是勾股数的整数倍的数也是勾股数,它们同样满足勾股定理逆定理的影响,错误的认为常见勾股数的平方(或倒数或算术平方根)它们同样满足勾股定理逆定理,从而得出错误的答案。
【正解】①
下列长度的三条线段能组成直角三角形的是( )
A.2, 3, 4 B.false C.5,11, 12 D.5,12, 13
【错解】B
【正解】D
【小结】判段三条线段能不能组成直角三角形,根据匀股定理的逆定理,只要验证两短边的平方和是否等于最长边的平方即可。
判定三角形全等时,忽略或误认了对应条件
如图,在Rt△ACB与Rt△DBA中,AC=DB,则Rt△ACB与Rt△DBA是否全等?
【错解】在Rt△ACB和Rt△DBA中,∵AC=DB,AB=BA,∴Rt△ACB≌Rt△DBA(HL).
【错因】在证明Rt△ABC≌Rt△DAB时,利用“HL”证明两个直角三角形全等,虽然也列举了两个条件,但AB和BA一个是Rt△ABC的斜边,另一个是是Rt△DAB的直角边,并不是两个三角形的对应边,判定全等的条件不够,所以不能证明两个三角形全等。
【正解】Rt△ACB和Rt△DBA不全等。
能判定两个直角三角形全等的是( )。
A.有一组锐角对应相等 B.两锐角对应相等
C.两条直角边对应相等 D.斜边与一直角边相等
【错解】D
【错因】错误的认为选项D中提到的一组直角边一定是一组对应边,从而利用“HL”判定两个直角三角形全等,忽视选项D中的直角边可能不是一组对应边,导致得出错误的结论。
【正解】C
下列说法中,正确的个数是( )
①斜边和一直角边对应相等的两个直角三角形全等;
②有两组边相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个 B.2个 C.3个 D.4个
【错解】C
【正解】B,根据HL得①对;②如果两个直角三角形一直角边和一斜边相等且另一直角边和一直角边相等,则这两个直角三角形不全等;由AAS或ASA得③正确;④显然错,选B
如图,已知AC⊥BD,垂足为O,AO=CO,BO=DO,则可得△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
【错解】A
【正解】C
【小结】利用“HL”判定两个三角形全等时,需要对应直角边相等,对应斜边相等。另外判定直角三角形全等,除了“HL”定理外,还可以是“SAS”、“ASA”、“AAS”、“SSS”。
推理过程不严谨,缺少逻辑性
解题过程中,由于语言不规范或缺少解题步骤导致错误。
如图,已知DE⊥AC于点E,BF⊥AC于点F,且AB=CD,DE=BF,求证:AE=CF.
【错解】∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.
在Rt△AFB和Rt△CED中,false,∴Rt△AFB≌Rt△CED(HL),∴AE=CF
【错因】题目中,由Rt△AFB≌Rt△CED不能直接推出AE=CF,因为它们不是全等三角形的对应边所以我们要逐步推导,不能省略中间的步骤。解题过程中步骤要尽可能的简洁明了,可有可无的步骤要去掉,但是必须有的步骤不能丢失,否则就会产生错误。
【正解】∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.
在Rt△AFB和Rt△CED中,false,∴Rt△AFB≌Rt△CED(HL),∴AE=CF
∴AF=CE,∴AF-EF=CE-EF,即AE=CF.
下列语句中,正确的有( )。
①两条直角边对应相等的两个直角三角形全等;②两边及第三边上的高对应相等的两个锐角三角形全等;③两边及其中一边上的高对应相等的两个锐角三角形全等;④两个锐角对应相等的两个直角三角形全等。
A.1个 B.2个 C.3个 D.4个
【错解】A或D
【正解】C
【小结】在几何推理中,一定要根据题意结合图形(无图形的题目,必要的话应先正确地画出图形),再依据条件严密地进行推理,切不可盲目地下结论。解答题我们一般要求简明,一些不必要的推理过程可以不写,但是一些必要的推理过程是必不可少的。
忽略定理运用的前提,误用角平分线性质定理解题
如图,已知AD⊥PC,BC⊥PD,AD与BC相交于点O,连接OP,且OD=OC,∠1=30°.求∠1的度数.
【错解】∵OD=OC,0A⊥PC,OB⊥PD,∴点O在∠DPC的平分线上,∴∠2=∠1=30°
【错因】利用角平分线的性质定理及其逆定理证明时,相等的线段须满足条件:①它们的公共端点在“角平分线上”,②它们的长度都是“点到角的两边的距离”,此处不符合条件②。
【正解】在△BOD 和△AOC中,∵false,∴△B0D≌△A0C(AAS),∴0B=0A
又∵0B⊥PD,OA⊥PC,∴PO是∠DPC的平分线,
已知点P是∠MON的平分线上一点,过O点P作AB上BNOP,分别交边OM,ON于A,B两点.求证:PA=PB
【错解】∵OP平分∠MON,AB⊥OP ∴PA=PB.
【正解】∵OP平分∠MON,∴∠AOP=∠BOP,∵AB⊥OP,∴∠APO=∠BPO=90°
又∵OP=OP,∴△AOP≌△BOP(ASA),∴PA=PB.
【小结】1.关于角平分线的性质定理:(1)只有同时满足“角平分线上的点”“到角的两边的距离”才能应用角平分线的性质定理得到“距离相等”;(2)角平分线性质中的“距离”是指点到射线的距离,是垂线段的长度.
2.关于角平分线的性质定理的逆定理:运用该定理时,要看清条件“到角两边的距离相等”(即两个垂直,且两条垂线段相等)
与角平分线的性质有关的方案选择受到思维定式的影响
,A,B是两个工厂,l1,l2是两余公路、现要在这个地区建一个加油站,要求加油站到A,B两厂的路程相等,且到两条路的距离相等,符合条件的点P有( )。
A.4个 B.3个 C.2个 D.1个
【错解】A或D
【错因】直线l1和l2相交形成了四个小于平角的角,故认为有四条角平分线与线段AB的金直平分线相交,得出四个交点,忽视了对顶角的平分线在同一条直线上,两条直线相交有且只有一个交点,故应该有两个交点。而选择只有一个交点是因为只考虑了一个内角的平分线。因此,在实际生活中,确定符合某个条件的点的位置时,注意分析问题要全面.
【正解】C
如图1-17,直线a、b、c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1个 B.2个 C.3个 D.4个
【错解】A
【正解】D
【小结】在实际问题中,确定到两“线”等距离点的位置(如建加油站、货物中转站、集市、水库等)的问题,常常用到角平分线的性质解决,尤其涉及作图探究的题目。运用“角的内部到为两边距离相等的点在这个角平分线上”,是寻找到两“线”等距离点的位置的一种比较简单的方法。
直角三角形的性质
性质1:直角三角形两锐角互余.
性质2:直角三角形斜边上的中线等于斜边的一半.
性质3:直角三角形中30o所对的直角边等于斜边的一半.
直角三角形的判定
判定1:有两个角互余的三角形是直角三角形.
判定2:一边上的中线等于这边的一半的三角形是直角三角形.
直角三角形的性质
勾股定理:如果直角三角形的两直角边为a 和b ,斜边为 c ,那么false.
直角三角形的判定
勾股定理逆定理:如果三角形三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
直角三角形全等的判断:
斜边和一直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边公理”或“HL”)
角平分线的性质定理:
角平分线上的点到角的两边的距离相等.
角平分线的性质定理的逆定理:
角平分线性质定理: 角平分线上的点到角的两边的距离相等.
忽略了运用直角三角形的性质的前提条件
在运用直角三角形的性质时,它的前提是在直角三角形中.如果三角形不是直角三角形,那么这些性质就不存在了,所以运用时要注意前提条件。
如图,在△ABC中,CD是AB边上的高,∠A=60°,则∠BCD的度数为( )
A.30° B.60° C.90° D.无法确定
【错解】B
【错因】在本题中没有指明△ABC是直角三角形,故不能利用直角三角形的性质进行计算。错解中想当然地认为△ABC是直角三角形,然后利用了直角三角形的性质,进而造成错解。
【正解】D
如图,在△ABC中,∠ABC=75°,从顶点B引射线BD与CA交于D点,使∠CDB=30°,BD=AD。求证:AD=2BC。
【错解】在△BCD中,∵∠CDB=30°,∴BC=12BD。∵BD=AD,∴BC=12AD,即AD=2BC
【错因】在本题中没有指明∠C=90O,故不能直接利用直角三角形的性质进行计算。在本题中应该先利用已知条件证出∠C=90O,再利用直角三角形的性质证明BD=2BC,进而得出AD=2BC
【正解】∵∠CDB=30°,BD=AD,∴∠A=∠ABD=12∠CDB=15°
∵∠ABC=75°,∴∠A+∠ABC=90°,∴∠C=90°
在Rt△BCD中,∵∠CDB=30°,∴BC=12BD
∵BD=AD ,∴BC=12AD,即AD=2BC。
在△ABC中,CD是AB边上的中线,若AB=6,则CD的长是( )
A.2 B.3 C.6 D.无法确定
【错解】B
【正解】D
【小结】“直角三角形两锐角互余”、“直角三角形斜边上的中线等于斜边的一半”、“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”这三个定理是直角三角形特有的性质时,所以在运用这几个性质时一定要注意前提条件是“在直角三角形中”。
误用直角三角形的性质
如图,在△ABC中,∠ACB=90°,BD=CD。求证:CD=AD。
【错解】在△ABC中,∵∠ACB=90°,
∴BD=CD,
∴CD=12AB=AD,
【错因】在本题已知条件中没有告诉点D为直角三角形斜边上的中点,故不能利用直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”来证明。
【正解】∵BD=CD,
∴∠BCD=∠B
∵∠ACB=90°,
∴∠BCD+∠ACD=90°,∠B+∠A=90°
∴∠ACD=∠A,
∴CD=AD
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,∠ABC的平分线为BD,且AD的长为15cm,求AC的长
【错解】在Rt△ABC中,∵∠C=90°,∠ABC=60°,BD平分∠A BC
∴∠A=30°,∠CBD=12∠ABC=30°
∴AC=2BC,BC=2CD,
∴AC=4CD,即CD=14AC
又∵AD+CD=AC 且 AD=15cm,∴AC=20cm
【正解】在Rt△ABC中,∵∠C=90°,∠ABC=60°,BD平分∠ABC
∴∠A=30°,∠CBD=∠ABD=12∠ABC=30°
∴CD =12BD, ∠A=∠ABD
∴AD=BD,∴CD=12AD
又∵AD+CD=AC且AD=15cm
∴AC=32AD= 22.5cm
【小结】运用直角三角形的性质解题时,如果审题不清或对直角三角形的性质理解不透彻的话,都会出现误用直角三角形的性质解题的现象,从而出现解题过程或解题结果出现错误。
因题目中没有图形而忽视分类讨论
对于一些求三角形(尤其是等腰三角形)的边长和角的度数的题目,当没有给出三角形的形状时,要注意分情况考虑,防止漏解.
在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,求∠C的度数.
【错解】△ABC中,∵BD是AC边高,∴∠ADB=90°,∴ ∠A=90°-∠ABD=90°-30°=60°
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°
又∵∠ABC=∠C,∴∠ABC=∠C=60°,即∠C=60°.
【错因】当题目中没有直接给出图形时,要注意分情况讨论,全面考虑.
三角形可能是锐角三角形,也可能是纯角三角形
【正解】当△ABC是锐角三角形时,如上图.
在△ABC中,BD是AC边上的高,∴∠ADB=90°,故∠A=90°-∠ABD=90°-30°=60°.
又∵∠A+∠ABC+∠C=180°,∴∠ABC+∠C=120°
又∵∠ABC=∠C,∴∠ABC=∠C=60°,即∠C=60°
.
当△ABC是钝角三角形时,如图,∵BD是△ABC 中AC边上的高,∴∠ADB=90°
在Rt△ABD中,∵∠ABD=30°,∴∠BAD=60°, ∴∠ABC+∠C=∠BAD=60°.
又∵∠ABC=∠C,∴∠C=30°
综上所述,∠C的度数为60°或30.
若等腰三角形一腰上的高与腰之比为1:2,则等腰三角形顶角的度数为( )
A.30° B.60°或120° C.30°或150° D.150°
【错解】A
【正解】C
已知在等腰△ABC中,AD⊥BC,垂足为点D,且AD=falseBC,求△ABC底角的度数。
【错解】如图,∵AB=AC,AD⊥BC,∴BD=CD.
∵AD=12BC,∴AD=BD=CD。
在Rt△ABD中,∠B=∠BAD=12 (180°-90°)=45°,
在Rt△ACD中,∠C=∠C40==12 (180°-90°)=45°
【正解】如图①,当AB=AC时,
∵AB=AC,AD⊥BC,∴∠B =∠C,BD=CD.
∵AD=12BC,∴AD=BD=CD。
在Rt△ABD中,∠B=∠BAD=12 (180°-90°)=45°,
当AC=BC时,
如图②,AD在△ABC外部时,∵AD=12BC,AC= BC,
∴AD=12AC,∠BAC=∠B,∴∠ACD=30°,
∵∠BAC+∠B=∠ACD,∴∠BAC=∠B=12×30°=15°
如图③,AD在△ABC内部时,∵AD=12BC,AC= BC,
∴AD=12AC, ∠BAC=∠B,∴∠C=30°,
∴∠BAC=∠B=12×(180°-∠C)=75°
综上所述,△ABC的底角的度数为45°或15°或75°.
(思考:为什么可以不讨论AB=BC时的情形?)
【小结】由于三角形的高可能在三角形内,也可能在三角形外,还有可能与三角形的边重合,所以在求涉及三角形(尤其是等腰三角形)高的边长和角的度数的题目时,若无图形,一般要进行分类讨论。
受思维定式的影响,误认为在RtΔABC中,c总表示斜边
在△ABC中,∠A=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=6,b=8,则c= .
【错解】10
【错因】对勾股定理理解不透彻,受勾股定理即勾股数的影响,误认为在RtΔABC中,c总表示斜边,从而求得错解
【正解】false
在△ABC中,∠A+∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,则c= .
【错解】5
【正解】false
【小结】在应用定理解题时,一定要弄清直角是哪一个角,进一步区别开斜边与直角边,不要误认为只要是在RtΔABC中,总有a2+b2=c2即false。
求不能确定斜边的直角三角形的第三边漏解
在直角三角形中,若已知边没指明是直角边,还是斜边,则要分情况进行讨论。
已知直角三角形的两边长分别为3,4,求第三边的长.
【错解】∵32+42=52,∴第三边长为5
【错因】习惯了“勾三股四弦五”的说法,即两直角边长为3和4时,斜边长为5.但这一说法的前提是以3,4为直角边长。而本题中并未说明,因此所求的第三边可能为斜边,也可能为直角边。
【正解】当两直角边长分别为3和4时,第三边长为false;
当斜边长为4,一条直角边长为3时,第三边长为false.
综上所述,第三边长为5或false.
已知一直角三角形的三边长分别为5,12,x,求以x为边长.的正方形面积。
【错解】由勾股定理得:x2=52+122=25+144=169,以x为边长的正方形面积为169。
【正解】∵x可能是斜边长,也有可能是直角边长,
∴由勾股定理得:x2=52+122=25+144=169或x2=122-52=144-25=119
∴以x为边长的正方形面积为169或119。
【小结】 已知直角三角形两条边长求第三条边的长时,如果题目中没有明确直角边和斜边,在利用勾股定理时要注意分情况讨论。
忽略了勾股定理的前提
利用勾股定理的前提条件是在直角三角形中,脱离直角三角形,就无法利用勾股定理。
已知在△ABC中,三边长为偶数,若AB>BC>AC,且AB=10,BC=8.试求AC的长.
【错解】在△ABC中,AB>BC>AC,AB是斜边。由勾股定理得AB2=AC2+BC2,即false
又∵AB=10,BC=8,∴false,∴AC的长是6.
【错因】勾股定理在直角三角形中才成立.本题中并没有说明△ABC是直角三角形,所以不能利用勾股定理求解.根据题设条件可以利用三角形的三边关系求解.
【正解】在△ABC中,∵AB=10,BC=8,∴2
如图,在△ABC中,AC=4,BC=3,则下列对AB的长的说法正确的是( )。
A.AB等于5 B.AB<7 C.AB>1 D.1
【正解】D
【小结】勾股定理是用于计算直角三角形边长的,所以在运用勾股定理时,必须先判定三角形是直角三角形,不能确定是直角三角形就不能套用勾股定理。受新知识及图形影响,没有认真思考,凭直感觉错误的套用新知识解题就会出现错解
不认真斟酌凭感觉解题,导致考虑不周到而出现错解
一架5m长的梯子,斜靠在一竖直的墙上,这时梯足距墙脚1.4m,若梯子的顶端下滑0.8m,则梯足将滑动
【错解】1(m)
【错因】本题没有建立相关模型,仅仅凭感觉就得出了答案,这往往是不可靠的。要想得出真解,首先根据描述建立模型:
【正解】如图,设梯子下滑之前顶端在A点,梯足在B点,墙脚设为C点,这样组成了一个Rt△ABC。梯子下滑后,梯子顶端在A'点,梯足在B'点,仍然构成Rt△A'B'C,只要求出B'C的长即可知道梯足滑动的距离。在Rt△ABC中,∠C=90°,AB=5m,BC=1.4m。
由勾股定理得AB2=AC2+BC2,∴false(m)。
在Rt△A'B'C中,∠C=90°,A'C=AC-AA'=4.8-0.8=4(m),A'B'=5m。
由勾股定理得A'B2=A'C2+B'C2,所以false(m)。
所以BB'=B'C-BC=3-1.4=1.6(m)。
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.false B.25 C.false D.35
【错解】A或C或D
【正解】将长方体展开,前、右两个侧面展开图如右上图所示,连接A、B,根据两点之间线段最短可知,线段AB的长即为蚂蚁爬行的最短距离;此时
如图,BD=10+5=15,AD=20,由勾股定理得:false,选B
【小结】对问题思考过于简单,就会对问题考虑不全面,产生错误的解答。
没有确定最长边而造成判断三角形形状时出错
已知三角形中三边长分别为2.5,2,l.5,试判断该三角形是不是直角三角形.
【错解】∵2.52+22≠1.52
∴该三角形不是直角三角形
【错因】受思维定式的限制,误认为勾股定理中的a,b,c分别是2.5,2,1.5,没有确定三条边中的最长边,导致出错.
【正解】∵1.52+22=2.52,∴该三角形是直角三角形.
判断由线段a,b,c组成的三角形是不是直角三角形,其中a=false,b=false,c=1。
【错解】∵false,∴该三角形不是直角三角形
【正解】∵false, ∴该三角形是直角三角形
【小结】在利用勾股定理逆定理判断三角形形状时,要确定三边中最长边,再由数量关系确定位置关系.
误认为以常见勾股数的平方(或倒数或算术平方根)为长的线段也能构成直角三角形
下列几组线段:①1,false,false;②32,42,52;③false,false,false;其中可以构成直角三角形的有 (填序号)
【错解】①②③
【错因】但凡是勾股数的整数倍的数也是勾股数,它们同样满足勾股定理逆定理的影响,错误的认为常见勾股数的平方(或倒数或算术平方根)它们同样满足勾股定理逆定理,从而得出错误的答案。
【正解】①
下列长度的三条线段能组成直角三角形的是( )
A.2, 3, 4 B.false C.5,11, 12 D.5,12, 13
【错解】B
【正解】D
【小结】判段三条线段能不能组成直角三角形,根据匀股定理的逆定理,只要验证两短边的平方和是否等于最长边的平方即可。
判定三角形全等时,忽略或误认了对应条件
如图,在Rt△ACB与Rt△DBA中,AC=DB,则Rt△ACB与Rt△DBA是否全等?
【错解】在Rt△ACB和Rt△DBA中,∵AC=DB,AB=BA,∴Rt△ACB≌Rt△DBA(HL).
【错因】在证明Rt△ABC≌Rt△DAB时,利用“HL”证明两个直角三角形全等,虽然也列举了两个条件,但AB和BA一个是Rt△ABC的斜边,另一个是是Rt△DAB的直角边,并不是两个三角形的对应边,判定全等的条件不够,所以不能证明两个三角形全等。
【正解】Rt△ACB和Rt△DBA不全等。
能判定两个直角三角形全等的是( )。
A.有一组锐角对应相等 B.两锐角对应相等
C.两条直角边对应相等 D.斜边与一直角边相等
【错解】D
【错因】错误的认为选项D中提到的一组直角边一定是一组对应边,从而利用“HL”判定两个直角三角形全等,忽视选项D中的直角边可能不是一组对应边,导致得出错误的结论。
【正解】C
下列说法中,正确的个数是( )
①斜边和一直角边对应相等的两个直角三角形全等;
②有两组边相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个 B.2个 C.3个 D.4个
【错解】C
【正解】B,根据HL得①对;②如果两个直角三角形一直角边和一斜边相等且另一直角边和一直角边相等,则这两个直角三角形不全等;由AAS或ASA得③正确;④显然错,选B
如图,已知AC⊥BD,垂足为O,AO=CO,BO=DO,则可得△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
【错解】A
【正解】C
【小结】利用“HL”判定两个三角形全等时,需要对应直角边相等,对应斜边相等。另外判定直角三角形全等,除了“HL”定理外,还可以是“SAS”、“ASA”、“AAS”、“SSS”。
推理过程不严谨,缺少逻辑性
解题过程中,由于语言不规范或缺少解题步骤导致错误。
如图,已知DE⊥AC于点E,BF⊥AC于点F,且AB=CD,DE=BF,求证:AE=CF.
【错解】∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.
在Rt△AFB和Rt△CED中,false,∴Rt△AFB≌Rt△CED(HL),∴AE=CF
【错因】题目中,由Rt△AFB≌Rt△CED不能直接推出AE=CF,因为它们不是全等三角形的对应边所以我们要逐步推导,不能省略中间的步骤。解题过程中步骤要尽可能的简洁明了,可有可无的步骤要去掉,但是必须有的步骤不能丢失,否则就会产生错误。
【正解】∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.
在Rt△AFB和Rt△CED中,false,∴Rt△AFB≌Rt△CED(HL),∴AE=CF
∴AF=CE,∴AF-EF=CE-EF,即AE=CF.
下列语句中,正确的有( )。
①两条直角边对应相等的两个直角三角形全等;②两边及第三边上的高对应相等的两个锐角三角形全等;③两边及其中一边上的高对应相等的两个锐角三角形全等;④两个锐角对应相等的两个直角三角形全等。
A.1个 B.2个 C.3个 D.4个
【错解】A或D
【正解】C
【小结】在几何推理中,一定要根据题意结合图形(无图形的题目,必要的话应先正确地画出图形),再依据条件严密地进行推理,切不可盲目地下结论。解答题我们一般要求简明,一些不必要的推理过程可以不写,但是一些必要的推理过程是必不可少的。
忽略定理运用的前提,误用角平分线性质定理解题
如图,已知AD⊥PC,BC⊥PD,AD与BC相交于点O,连接OP,且OD=OC,∠1=30°.求∠1的度数.
【错解】∵OD=OC,0A⊥PC,OB⊥PD,∴点O在∠DPC的平分线上,∴∠2=∠1=30°
【错因】利用角平分线的性质定理及其逆定理证明时,相等的线段须满足条件:①它们的公共端点在“角平分线上”,②它们的长度都是“点到角的两边的距离”,此处不符合条件②。
【正解】在△BOD 和△AOC中,∵false,∴△B0D≌△A0C(AAS),∴0B=0A
又∵0B⊥PD,OA⊥PC,∴PO是∠DPC的平分线,
已知点P是∠MON的平分线上一点,过O点P作AB上BNOP,分别交边OM,ON于A,B两点.求证:PA=PB
【错解】∵OP平分∠MON,AB⊥OP ∴PA=PB.
【正解】∵OP平分∠MON,∴∠AOP=∠BOP,∵AB⊥OP,∴∠APO=∠BPO=90°
又∵OP=OP,∴△AOP≌△BOP(ASA),∴PA=PB.
【小结】1.关于角平分线的性质定理:(1)只有同时满足“角平分线上的点”“到角的两边的距离”才能应用角平分线的性质定理得到“距离相等”;(2)角平分线性质中的“距离”是指点到射线的距离,是垂线段的长度.
2.关于角平分线的性质定理的逆定理:运用该定理时,要看清条件“到角两边的距离相等”(即两个垂直,且两条垂线段相等)
与角平分线的性质有关的方案选择受到思维定式的影响
,A,B是两个工厂,l1,l2是两余公路、现要在这个地区建一个加油站,要求加油站到A,B两厂的路程相等,且到两条路的距离相等,符合条件的点P有( )。
A.4个 B.3个 C.2个 D.1个
【错解】A或D
【错因】直线l1和l2相交形成了四个小于平角的角,故认为有四条角平分线与线段AB的金直平分线相交,得出四个交点,忽视了对顶角的平分线在同一条直线上,两条直线相交有且只有一个交点,故应该有两个交点。而选择只有一个交点是因为只考虑了一个内角的平分线。因此,在实际生活中,确定符合某个条件的点的位置时,注意分析问题要全面.
【正解】C
如图1-17,直线a、b、c表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1个 B.2个 C.3个 D.4个
【错解】A
【正解】D
【小结】在实际问题中,确定到两“线”等距离点的位置(如建加油站、货物中转站、集市、水库等)的问题,常常用到角平分线的性质解决,尤其涉及作图探究的题目。运用“角的内部到为两边距离相等的点在这个角平分线上”,是寻找到两“线”等距离点的位置的一种比较简单的方法。
同课章节目录
