二次函数的应用(学校教研)
图片预览

文档简介
我们所解决的每一个问题,将成为一种模式,用于解决其他问题。
二次函数的应用
【学习目标】会运用二次函数求实际问题中的最大值或最小值。
【学习过程】
学前准备
1.已知二次函数,当 时,取最 值 。
2.二次函数的图象开口 ,当 时,取最
值,它的图象过点(0, )。
3.二次函数,当 时,取最大(小)值 ;
4.二次函数,当 时,取最大(小)值 。
灵活运用
1.“建模”——构造二次函数模型
如图,用12 m长的铝合金材料,做一个有一条横档的矩形窗框。为使透进的光线最多,窗子的长和宽应各为多少?
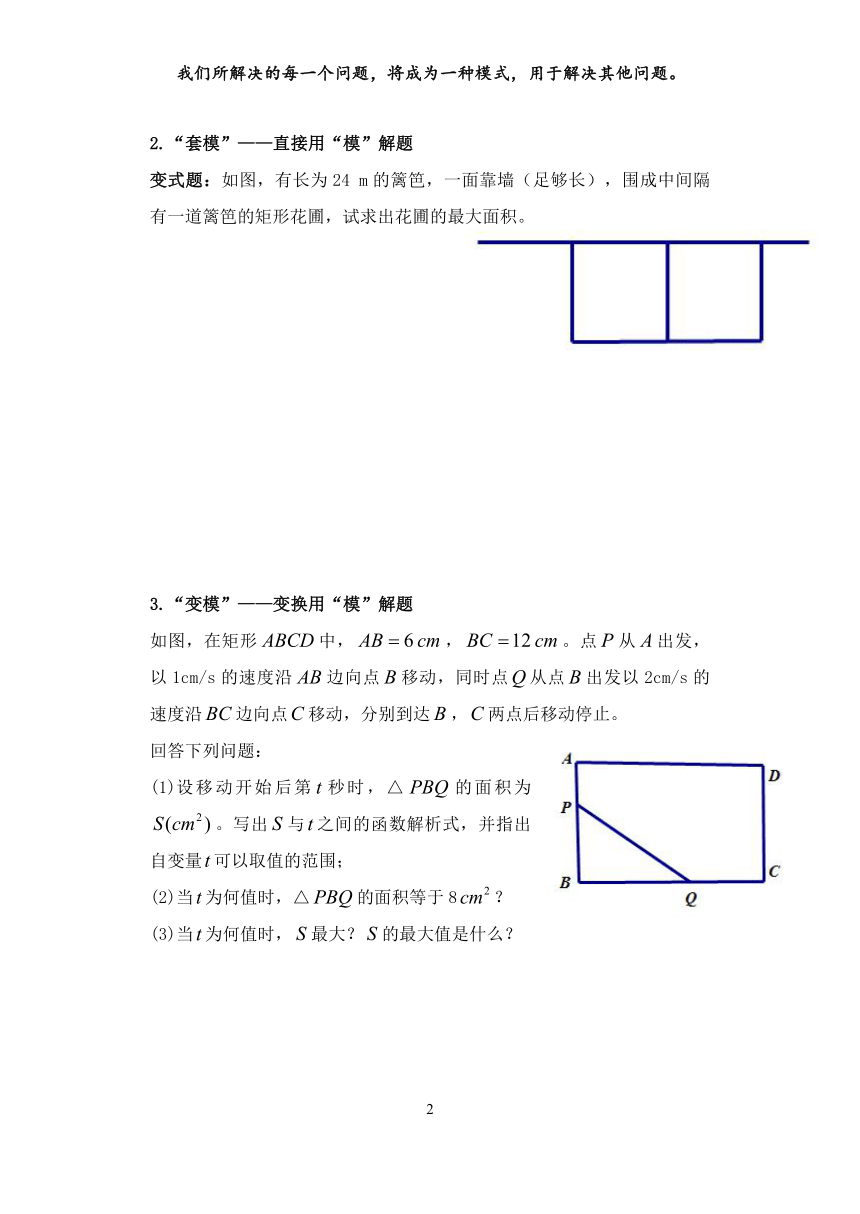
2.“套模”——直接用“模”解题
变式题:如图,有长为24 m的篱笆,一面靠墙(足够长),围成中间隔有一道篱笆的矩形花圃,试求出花圃的最大面积。
3.“变模”——变换用“模”解题
如图,在矩形中,,。点从出发,以1cm/s的速度沿边向点移动,同时点从点出发以2cm/s的速度沿边向点移动,分别到达,两点后移动停止。
回答下列问题:
设移动开始后第秒时,△的面积为。写出与之间的函数解析式,并指出自变量可以取值的范围;
当为何值时,△的面积等于8?
当为何值时,最大?的最大值是什么?
练习:如图,在Δ中,8cm,6cm,∠B=90°,点从点开始沿边向点以2厘米/秒的速度移动,点从点开始沿边向点以1厘米/秒的速度移动,如果,分别从,同时出发,几秒后Δ的面积最大?最大面积是多少?
拓展提升:某果园收获了柑橘65吨,如果直接出售,市场价格为每吨
1 500元;如果把柑橘储藏起来,每周会烂掉2吨,但每吨价格也将上涨120元,何时出售才能获利最大?
4.小结反思
通过这节课的学习,你有哪些收获?
对这节课的学习,你还有什么想法吗?
5.布置作业
课本53页综合练习,检测站
三、课后延伸
运动中的二次函数问题包括隧道问题、拱门问题、喷泉问题、扔铅球问题等。
如图,某企业的大门呈抛物线形,大门底部的宽为4 m,顶端距离地面的高度为4.4 m,一辆满载货物的汽车要通过大门,货物顶部距地面2.8 m,装货宽度为2.4 m,这辆汽车能否顺利通过大门?为什么?
4
二次函数的应用
【学习目标】会运用二次函数求实际问题中的最大值或最小值。
【学习过程】
学前准备
1.已知二次函数,当 时,取最 值 。
2.二次函数的图象开口 ,当 时,取最
值,它的图象过点(0, )。
3.二次函数,当 时,取最大(小)值 ;
4.二次函数,当 时,取最大(小)值 。
灵活运用
1.“建模”——构造二次函数模型
如图,用12 m长的铝合金材料,做一个有一条横档的矩形窗框。为使透进的光线最多,窗子的长和宽应各为多少?
2.“套模”——直接用“模”解题
变式题:如图,有长为24 m的篱笆,一面靠墙(足够长),围成中间隔有一道篱笆的矩形花圃,试求出花圃的最大面积。
3.“变模”——变换用“模”解题
如图,在矩形中,,。点从出发,以1cm/s的速度沿边向点移动,同时点从点出发以2cm/s的速度沿边向点移动,分别到达,两点后移动停止。
回答下列问题:
设移动开始后第秒时,△的面积为。写出与之间的函数解析式,并指出自变量可以取值的范围;
当为何值时,△的面积等于8?
当为何值时,最大?的最大值是什么?
练习:如图,在Δ中,8cm,6cm,∠B=90°,点从点开始沿边向点以2厘米/秒的速度移动,点从点开始沿边向点以1厘米/秒的速度移动,如果,分别从,同时出发,几秒后Δ的面积最大?最大面积是多少?
拓展提升:某果园收获了柑橘65吨,如果直接出售,市场价格为每吨
1 500元;如果把柑橘储藏起来,每周会烂掉2吨,但每吨价格也将上涨120元,何时出售才能获利最大?
4.小结反思
通过这节课的学习,你有哪些收获?
对这节课的学习,你还有什么想法吗?
5.布置作业
课本53页综合练习,检测站
三、课后延伸
运动中的二次函数问题包括隧道问题、拱门问题、喷泉问题、扔铅球问题等。
如图,某企业的大门呈抛物线形,大门底部的宽为4 m,顶端距离地面的高度为4.4 m,一辆满载货物的汽车要通过大门,货物顶部距地面2.8 m,装货宽度为2.4 m,这辆汽车能否顺利通过大门?为什么?
4
