3.4.2合并同类项课件

(共20张PPT)
3.4合并同类项-（1）
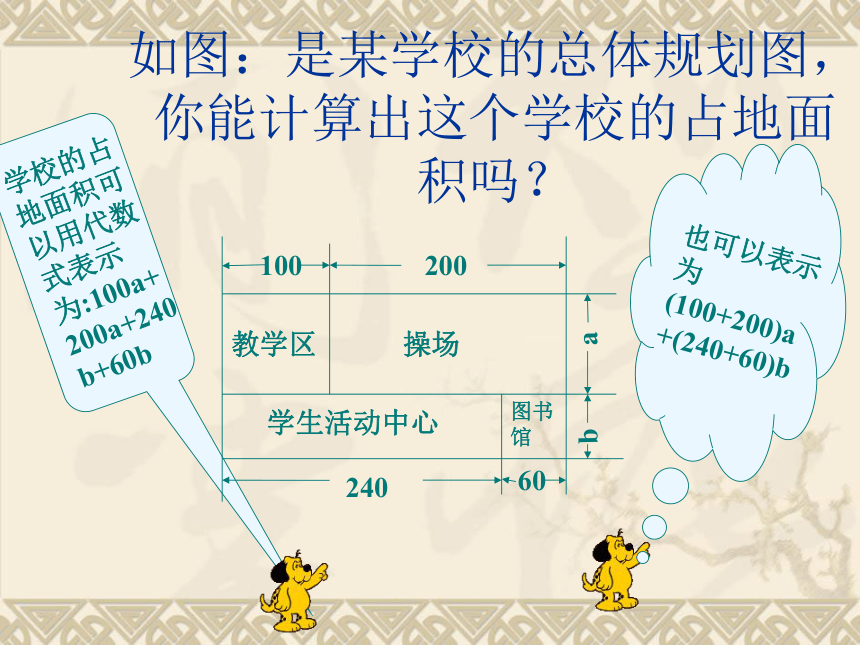
如图：是某学校的总体规划图，你能计算出这个学校的占地面积吗？
100
200
教学区
操场
学生活动中心
图书馆
240
60
a
b
学校的占地面积可以用代数式表示为:100a+200a+240b+60b
也可以表示为(100+200)a+(240+60)b
可以看出：
100a+200a+240b+60b=(100+200)a+(240+60)b
由此我们可以看出：在计算100a+200a时，可以把它们的系数相加，再乘以a,既100a+200a=（100+200）a;同样在计算240b+60b=（240+60）b.
在这里，你能说出100a与200a;240b与60b;5ab2 与-13ab2 ;-9x2y3与5x2y3有什么共同的特点？
什么是同类项？
（1）分类游戏
猫、松树、狗、小麦、向日葵、大象
猫、狗、大象
动物
植物
松树、小麦、向日葵
同类：具有共同特征
（2）游戏：找同类项朋友
3a2b+2ab2-ab2-5a2b
3a+2b-5a-b
1、字母相同
2、相同字母的指数也相同
同类项条件：
3-4ab-b2+5
几个常数项也是同类项。
注意
合并同类项，并说明你计算的理由：
(1)7a-5a=______;理由：_________
(2)4x2+x2=____;理由：___________
(3)5ab2-13ab2=_____;理由：_______
(4) -9x2y3+5x2y3=____;理由：_____
合并同类项的法则：
把同类项的系数相加，所得的结果做为系数，字母和字母的指数不变。
例题评讲
例1: 合并同类项
(1)-3x+2y-5x-7y
(2) m3-3m2n- m3 +2nm2-7+ 2m3
解:(1) -3x+2y-5x-7y
=(-3x -5x)+(2y -7y)
=(-3-5)x+(2-7)y
=-8x-5y
(2) m3-3m2n- m3 +2nm2-7+ 2m3
=( m3 - m3 +2m3 )+(-3m2n +2nm2)-7
=( 1-1+2) m3+(-3+2)m2n-7
= 2 m3-m2n-7
例题评讲
例1: 合并同类项
(1)-3x+2y-5x-7y
(2) m3-3m2n- m3 +2nm2-7+ 2m3
加法交换律、结合律乘法对加法的分配律、有理数加法法则
知识点
解：(2) m3-3m2n- m3 +2nm2-7+ 2m3
=( m3 - m3 +2m3 )+(-3m2n +2nm2)-7
=( -1+2) m3+(-3+2)m2n-7
= m3-m2n-7
下列各题的结果是否正确？
如有错误，请指出错误的地方。
1、16y2 - 7y2=9
2、7x – 5x=2x2
3、3x+ 3y=6xy
4、19a2 b- 9b2a=10
合并同类项时，
字母不变。应为
16y2 - 7y2=9y2
合并同类项时，
字母的指数不变。应为
7x – 5x=2x
没有同类项可合并
没有同类项可合并
课堂练习
例2：合并同类项
- 4ab+8a - 2b2 - 9ab – 8a
解：- 4ab+8 a- 2b2 - 9ab – 8a
=(- 4ab - 9ab )
=( )ab+( )a
= - 13ab
合并同类项步骤：
1、划线，找出各组同类项；
2、把同类项写在一起；
3、合并同类项。
注意：不要漏写没有同类项的项，如- 2b2 。
+( +8a – 8a )
- 2b2
- 4 - 9
+8 – 8
- 2b2
- 2b2
例题评讲
2、3a2b+2ab2-ab2-5a2b
1、3a+2b-5a-b
3、3-4ab-b2+5
4、3b-3a3+1+a3-2b
5、2y+6y+2xy-5
课堂练习
通过以上的练习
你可以找出合并同类项的要点是什么？
一变一不变
一变就是系数要变
（新系数变为原来各系数的代数和）
一不变就是字母和字母的指数不变
（原来的字母和字母的指数照抄）
拓展应用：
1、已知： 与
是同类项，求 5m+3n 的值 .
2
_
3
x(3m-1)y3
-
1
_
4
x5y(2n+1)
2
_
3
x(3m-1)y3
-
1
_
4
x5y(2n+1)
解：∵ 与 是同类项
∴ 3m-1=5 , 2n+1=3
∴ m=2 , n=1
∴5m+3n=5×2+3×1
=10+3
=13
2、合并同类项： (a-b)2-3(a-b)-2(a-b)2+7(a-b)
3、 已知: a+b= -
求代数式 3(a+b)-5a-5b+7 的值
拓展应用：
当堂检测
1：合并同类项
2、光明中学初一学生有（a+b)人，初二学生 比
初一学生多(a-5)人，初三学生有2b人，那么该
校初中学生共有多少人？
3、已知6x2y与-2xmyn为同类项，求m2+3mn的值。
4、有这样一道题：当 a=13.58, b=9.07 时，求多项式
7a3 - 6a3b+3a2b+3a3+6a3b - 3a2b - 10a3的值。
有同学指出：题目中的条件a=13.58, b=9.07是多余
的。你认为这种说法有道理吗？
当堂检测
合并同类项小结：
本节课的问题
1、什么是同类项？
2、怎样合并同类项？
3、合并同类项有什么用处？
答：所含字母相同，且相同字母的指数也相同
的项叫做同类项。
答：把同类项的系数相加，字母和字母的指数不变。
答：可以简化代数式。
习题3.4 第2题、第3题（1）（2）（3）