圆周角定理及推论同步练习
图片预览





文档简介
(共12张PPT)
圆周角定理及推论
练习题
资中县板栗中心学校 张怀扬
·
A
B
C1
O
C2
C3
圆周角定理及推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定 理
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
推 论
1、⊙O的半径为5,圆心的坐标为
(0,0)点P的坐标为(4,2),
点A的坐标为(4,-3),则点P
与⊙O的位置关系是 ,点A在
⊙O的 。
2、一个点与定圆上最近的距离为
4㎝,最远点的距离为9㎝,则此圆
的半径为 。
A(4,-3)
x
y
o
.
.
P
(4,2)
1题
5
3
4
2
4
5
2
.
.
O
P
4㎝
9㎝
A
B
2题
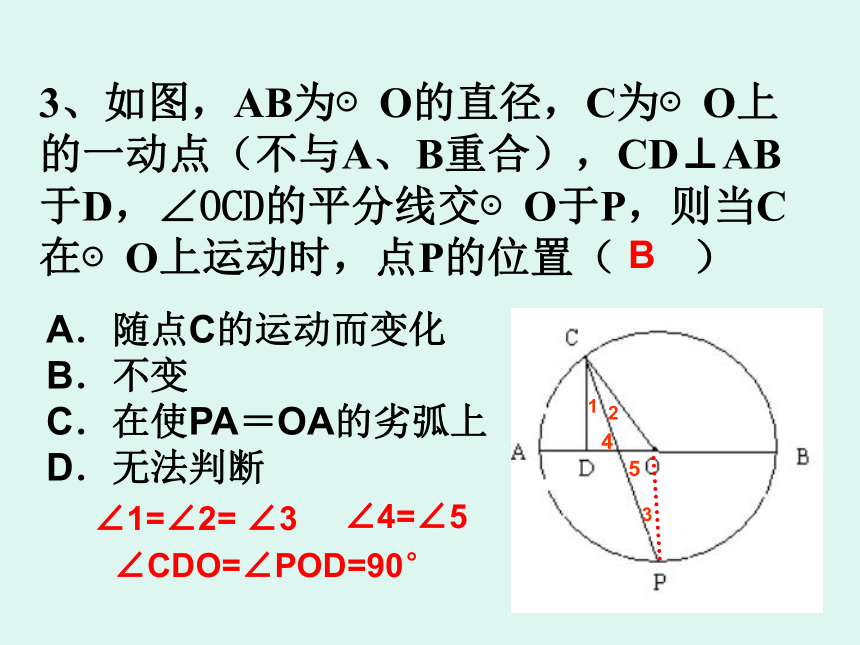
3、如图,AB为⊙O的直径,C为⊙O上
的一动点(不与A、B重合),CD⊥AB
于D,∠OCD的平分线交⊙O于P,则当C
在⊙O上运动时,点P的位置( )
A.随点C的运动而变化
B.不变
C.在使PA=OA的劣弧上
D.无法判断
1
2
3
4
5
B
∠1=∠2= ∠3
∠4=∠5
∠CDO=∠POD=90°
O
A
B
C
D
4.如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D。已知CD=2cm,AD=1cm,求AB的长.
解一
解二
连接CO,利用勾股定理
求出半径:r2=(r-1)2+22
r
r-1
2
连接CA,CB利用射影定理
求出DB
CD2=AD · DB
5.如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,求⊙O的直径.
●O
A
C
B
E
6、以⊙O的直径BC为一边作等边三角
形ABC,AB、AC交⊙O于D、E两点,
求证:BD=DE=EC。
7、如图,△ABC内接于圆,D是
的中点,AD交BC于E
求证:AB·AC=AE·AD。
2
1
△ABD∽ △AEC
分析:要证AB · AC = AE · AD
∠1=∠2
∠C=∠D
AC
AD
AE
AB
=
8、如图,在⊙O中,弦AB、CD垂直相
交于点E,求证:∠BOC+∠AOD=1800。
1
3
2
∠BOC+∠AOD=∠1+∠3
=2∠2+2∠ABD
=2(∠2+∠ABD)
=2 ×900
=1800
9、已知:△ABC为⊙O的内接三角形,
⊙O的直径BD交AC于E。AF⊥BD于
F,延长AF交BC于G,
求证:AB2=BG·BC。
分析:要证AB2=BG·BC
△ABG∽ △CBA
1
∠ABG =∠CBA
∠1= ∠C
?
连接BH,利用等孤所对的圆周角相等:
2
∠1= ∠2=∠C
10、如图,以△ABC的BC边为直径的半
圆交AB于D,交AC于E,过E作EF⊥BC,
垂足为F,且BF:FC=5:1,AB=8,
AE=2,求EC的长。
分析:连接BE,得AC BE
则BE2=AB2-AE2=60
由射影定理可知BE2=BF·BC
即 BC2=60
6
5
BC2=72
CE2=BC2-BE2=12
圆周角定理及推论
练习题
资中县板栗中心学校 张怀扬
·
A
B
C1
O
C2
C3
圆周角定理及推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定 理
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
推 论
1、⊙O的半径为5,圆心的坐标为
(0,0)点P的坐标为(4,2),
点A的坐标为(4,-3),则点P
与⊙O的位置关系是 ,点A在
⊙O的 。
2、一个点与定圆上最近的距离为
4㎝,最远点的距离为9㎝,则此圆
的半径为 。
A(4,-3)
x
y
o
.
.
P
(4,2)
1题
5
3
4
2
4
5
2
.
.
O
P
4㎝
9㎝
A
B
2题
3、如图,AB为⊙O的直径,C为⊙O上
的一动点(不与A、B重合),CD⊥AB
于D,∠OCD的平分线交⊙O于P,则当C
在⊙O上运动时,点P的位置( )
A.随点C的运动而变化
B.不变
C.在使PA=OA的劣弧上
D.无法判断
1
2
3
4
5
B
∠1=∠2= ∠3
∠4=∠5
∠CDO=∠POD=90°
O
A
B
C
D
4.如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D。已知CD=2cm,AD=1cm,求AB的长.
解一
解二
连接CO,利用勾股定理
求出半径:r2=(r-1)2+22
r
r-1
2
连接CA,CB利用射影定理
求出DB
CD2=AD · DB
5.如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,求⊙O的直径.
●O
A
C
B
E
6、以⊙O的直径BC为一边作等边三角
形ABC,AB、AC交⊙O于D、E两点,
求证:BD=DE=EC。
7、如图,△ABC内接于圆,D是
的中点,AD交BC于E
求证:AB·AC=AE·AD。
2
1
△ABD∽ △AEC
分析:要证AB · AC = AE · AD
∠1=∠2
∠C=∠D
AC
AD
AE
AB
=
8、如图,在⊙O中,弦AB、CD垂直相
交于点E,求证:∠BOC+∠AOD=1800。
1
3
2
∠BOC+∠AOD=∠1+∠3
=2∠2+2∠ABD
=2(∠2+∠ABD)
=2 ×900
=1800
9、已知:△ABC为⊙O的内接三角形,
⊙O的直径BD交AC于E。AF⊥BD于
F,延长AF交BC于G,
求证:AB2=BG·BC。
分析:要证AB2=BG·BC
△ABG∽ △CBA
1
∠ABG =∠CBA
∠1= ∠C
?
连接BH,利用等孤所对的圆周角相等:
2
∠1= ∠2=∠C
10、如图,以△ABC的BC边为直径的半
圆交AB于D,交AC于E,过E作EF⊥BC,
垂足为F,且BF:FC=5:1,AB=8,
AE=2,求EC的长。
分析:连接BE,得AC BE
则BE2=AB2-AE2=60
由射影定理可知BE2=BF·BC
即 BC2=60
6
5
BC2=72
CE2=BC2-BE2=12
