2020-2021鲁教版(五四制)数学八年级下册 -第六章 特殊平行四边形 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021鲁教版(五四制)数学八年级下册 -第六章 特殊平行四边形 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览

文档简介
2020-2021学年鲁教版数学八年级下册同步练习-第六章 特殊平行四边形
一、选择题
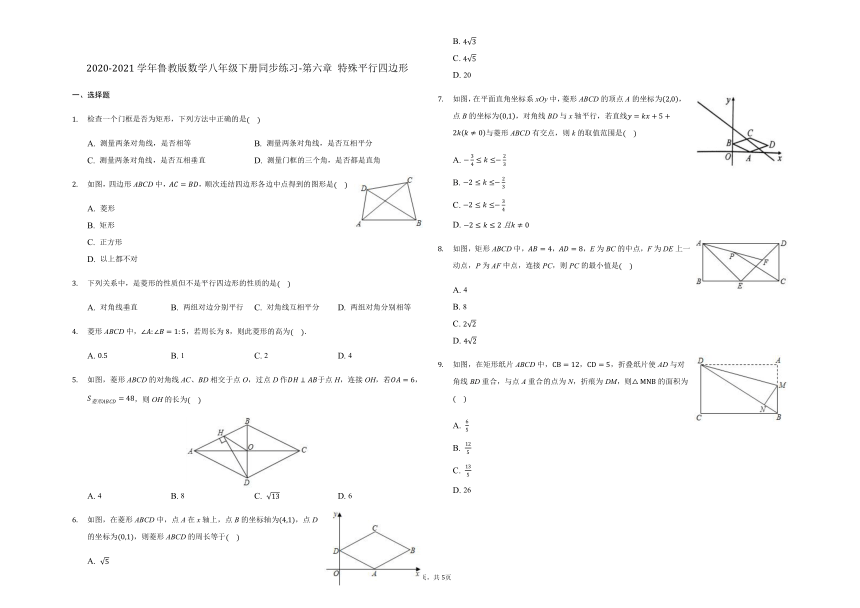
检查一个门框是否为矩形,下列方法中正确的是(????)
A. 测量两条对角线,是否相等 B. 测量两条对角线,是否互相平分
C. 测量两条对角线,是否互相垂直 D. 测量门框的三个角,是否都是直角
如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是(????)
A. 菱形
B. 矩形
C. 正方形
D. 以上都不对
下列关系中,是菱形的性质但不是平行四边形的性质的是(????)
A. 对角线垂直 B. 两组对边分别平行 C. 对角线互相平分 D. 两组对角分别相等
菱形ABCD中,∠A:∠B=1:5,若周长为8,则此菱形的高为(????).
A. 0.5 B. 1 C. 2 D. 4
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为(????)
A. 4 B. 8 C. 13 D. 6
如图,在菱形ABCD中,点A在x轴上,点B的坐标轴为(4,1),点D的坐标为(0,1),则菱形ABCD的周长等于(????)
A. 5
B. 43
C. 45
D. 20
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为2,0,点B的坐标为0,1,对角线BD与x轴平行,若直线y=kx+5+2kk≠0与菱形ABCD有交点,则k的取值范围是(????)
A. ?34≤k≤?23
B. ?2≤k≤?23
C. ?2≤k≤?34
D. ?2≤k≤2且k≠0
如图,矩形ABCD中,AB=4,AD=8,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是(????)
A. 4
B. 8
C. 22
D. 42
如图,在矩形纸片ABCD中,CB=12,CD=5,折叠纸片使AD与对角线BD重合,与点A重合的点为N,折痕为DM,则△MNB的面积为(????)
A. 65
B. 125
C. 135
D. 26
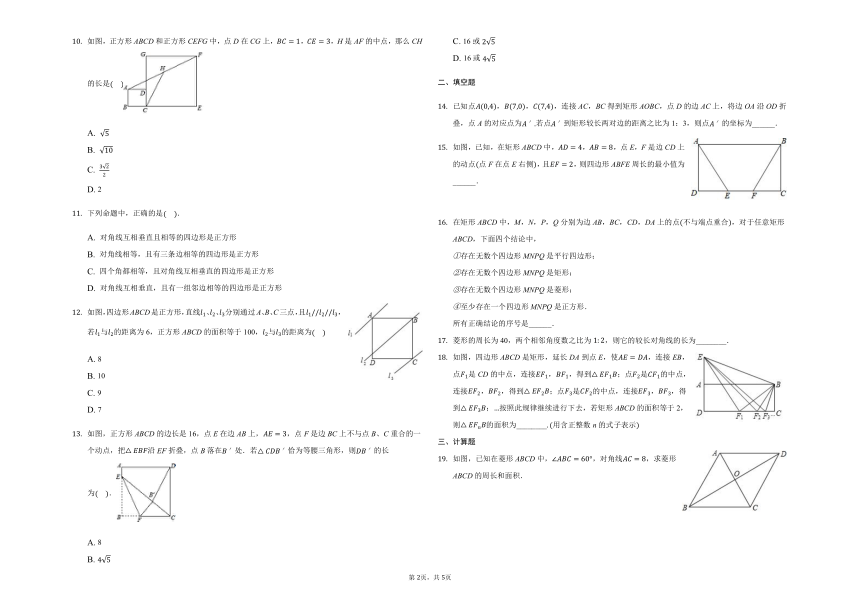
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是(????)
A. 5
B. 10
C. 322
D. 2
下列命题中,正确的是(????).
A. 对角线互相垂直且相等的四边形是正方形
B. 对角线相等,且有三条边相等的四边形是正方形
C. 四个角都相等,且对角线互相垂直的四边形是正方形
D. 对角线互相垂直,且有一组邻边相等的四边形是正方形
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1//l2//l3,若l1与l2的距离为6,正方形ABCD的面积等于100,l2与l3的距离为(????)
A. 8
B. 10
C. 9
D. 7
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为(????).
A. 8
B. 45
C. 16或25
D. 16或45
二、填空题
已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应点为A′.若点A′到矩形较长两对边的距离之比为1:3,则点A′的坐标为______.
如图,已知,在矩形ABCD中,AD=4,AB=8,点E,F是边CD上的动点(点F在点E右侧),且EF=2,则四边形ABFE周长的最小值为______.
在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
所有正确结论的序号是______.
菱形的周长为40,两个相邻角度数之比为1:2,则它的较长对角线的长为________.
如图,四边形ABCD是矩形,延长DA到点E,使AE=DA,连接EB,点F1是CD的中点,连接EF1,BF1,得到△EF1B;点F2是CF1的中点,连接EF2,BF2,得到△EF2B;点F3是CF2的中点,连接EF3,BF3,得到△EF3B;…按照此规律继续进行下去,若矩形ABCD的面积等于2,则△EFnB的面积为________.(用含正整数n的式子表示)
三、计算题
如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
已知菱形ABCD和菱形DEFG有公共的顶点D,C点在DE上,且∠ADC=∠EDG,连接AE,CG,如图1.
(1)试猜想AE与CG有怎样的数量关系(直接写出关系,不用证明);
(2)将菱形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;
(3)在(2)的条件下,如果∠ADC=∠EDG=90°,如图3,你认为AE和CG是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
答案
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】A
11.【答案】C
12.【答案】A
13.【答案】D
14.【答案】(7,3)或(15,1)或(23,?2)
15.【答案】20
16.【答案】①②③
17.【答案】103
18.【答案】2n+12n
19.【答案】解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=8.
∴菱形ABCD的周长=4×8=32,
∵BO=82?42=43,
∴BD=2BO=83,
∴菱形ABCD的面积=12×8×83=323.
20.【答案】(1)证明:在菱形ABCD中,OC=12AC.
∵DE:AC=1:2,
∴DE=OC,
∵DE//AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=AD2?AO2=22?12=3.
在Rt△ACE中,
AE=AC2+CE2=22+(3)2=7.
21.【答案】(1)证明∵AC=9??AB=12??BC=15,
∴AC2+AB2=225,BC2=225,
∴AC2+AB2=BC2,
∴△ABC为直角三角形,∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90°,
∴四边形AGPH是矩形;
(2)存在.理由如下:
连结AP.
∵四边形AGPH是矩形,
∴GH=AP,
当AP⊥BC时,此时AP的值最小,
由S△ACB=12AC·AB=12AP·BC,
∴9×12=15?AP,
∴AP=365,
∴GH的最小值为365.
22.【答案】解:(1)AE=CG,
理由如下:∵四边形ABCD和四边形DEFG都是菱形,
∴DA=DC,DE=DG,
在△DAE和△DCG中,
DA=DC∠ADE=∠CDGDE=DG,
∴△DAE≌△DCG(SAS),
∴AE=CG;
(2)成立,
理由如下:∵∠ADC=∠EDG,
∴∠ADC?∠EDC=∠EDG?∠EDC,即∠ADE=∠CDG,
在△DAE和△DCG中,
DA=DC∠ADE=∠CDGDE=DG,
∴△DAE≌△DCG(SAS),
∴AE=CG;
(3)AE⊥CG,
理由如下:延长线段AE、GC交于点H,
∵AD//BC,
∴∠CEH=∠DAE,
由(2)可知,△DAE≌△DCG,
∴∠DAE=∠DCG,
∴∠CEH=∠DCG,
∵四边形ABCD是菱形,∠ADC=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°,
∴∠ECH+∠DCG=90°,
∴∠ECH+∠CEH=90°,
∴∠CHE=90°,
∴AE⊥CG.
一、选择题
检查一个门框是否为矩形,下列方法中正确的是(????)
A. 测量两条对角线,是否相等 B. 测量两条对角线,是否互相平分
C. 测量两条对角线,是否互相垂直 D. 测量门框的三个角,是否都是直角
如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是(????)
A. 菱形
B. 矩形
C. 正方形
D. 以上都不对
下列关系中,是菱形的性质但不是平行四边形的性质的是(????)
A. 对角线垂直 B. 两组对边分别平行 C. 对角线互相平分 D. 两组对角分别相等
菱形ABCD中,∠A:∠B=1:5,若周长为8,则此菱形的高为(????).
A. 0.5 B. 1 C. 2 D. 4
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为(????)
A. 4 B. 8 C. 13 D. 6
如图,在菱形ABCD中,点A在x轴上,点B的坐标轴为(4,1),点D的坐标为(0,1),则菱形ABCD的周长等于(????)
A. 5
B. 43
C. 45
D. 20
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为2,0,点B的坐标为0,1,对角线BD与x轴平行,若直线y=kx+5+2kk≠0与菱形ABCD有交点,则k的取值范围是(????)
A. ?34≤k≤?23
B. ?2≤k≤?23
C. ?2≤k≤?34
D. ?2≤k≤2且k≠0
如图,矩形ABCD中,AB=4,AD=8,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是(????)
A. 4
B. 8
C. 22
D. 42
如图,在矩形纸片ABCD中,CB=12,CD=5,折叠纸片使AD与对角线BD重合,与点A重合的点为N,折痕为DM,则△MNB的面积为(????)
A. 65
B. 125
C. 135
D. 26
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是(????)
A. 5
B. 10
C. 322
D. 2
下列命题中,正确的是(????).
A. 对角线互相垂直且相等的四边形是正方形
B. 对角线相等,且有三条边相等的四边形是正方形
C. 四个角都相等,且对角线互相垂直的四边形是正方形
D. 对角线互相垂直,且有一组邻边相等的四边形是正方形
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1//l2//l3,若l1与l2的距离为6,正方形ABCD的面积等于100,l2与l3的距离为(????)
A. 8
B. 10
C. 9
D. 7
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为(????).
A. 8
B. 45
C. 16或25
D. 16或45
二、填空题
已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应点为A′.若点A′到矩形较长两对边的距离之比为1:3,则点A′的坐标为______.
如图,已知,在矩形ABCD中,AD=4,AB=8,点E,F是边CD上的动点(点F在点E右侧),且EF=2,则四边形ABFE周长的最小值为______.
在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
所有正确结论的序号是______.
菱形的周长为40,两个相邻角度数之比为1:2,则它的较长对角线的长为________.
如图,四边形ABCD是矩形,延长DA到点E,使AE=DA,连接EB,点F1是CD的中点,连接EF1,BF1,得到△EF1B;点F2是CF1的中点,连接EF2,BF2,得到△EF2B;点F3是CF2的中点,连接EF3,BF3,得到△EF3B;…按照此规律继续进行下去,若矩形ABCD的面积等于2,则△EFnB的面积为________.(用含正整数n的式子表示)
三、计算题
如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
已知菱形ABCD和菱形DEFG有公共的顶点D,C点在DE上,且∠ADC=∠EDG,连接AE,CG,如图1.
(1)试猜想AE与CG有怎样的数量关系(直接写出关系,不用证明);
(2)将菱形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;
(3)在(2)的条件下,如果∠ADC=∠EDG=90°,如图3,你认为AE和CG是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
答案
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】A
11.【答案】C
12.【答案】A
13.【答案】D
14.【答案】(7,3)或(15,1)或(23,?2)
15.【答案】20
16.【答案】①②③
17.【答案】103
18.【答案】2n+12n
19.【答案】解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=8.
∴菱形ABCD的周长=4×8=32,
∵BO=82?42=43,
∴BD=2BO=83,
∴菱形ABCD的面积=12×8×83=323.
20.【答案】(1)证明:在菱形ABCD中,OC=12AC.
∵DE:AC=1:2,
∴DE=OC,
∵DE//AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=AD2?AO2=22?12=3.
在Rt△ACE中,
AE=AC2+CE2=22+(3)2=7.
21.【答案】(1)证明∵AC=9??AB=12??BC=15,
∴AC2+AB2=225,BC2=225,
∴AC2+AB2=BC2,
∴△ABC为直角三角形,∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90°,
∴四边形AGPH是矩形;
(2)存在.理由如下:
连结AP.
∵四边形AGPH是矩形,
∴GH=AP,
当AP⊥BC时,此时AP的值最小,
由S△ACB=12AC·AB=12AP·BC,
∴9×12=15?AP,
∴AP=365,
∴GH的最小值为365.
22.【答案】解:(1)AE=CG,
理由如下:∵四边形ABCD和四边形DEFG都是菱形,
∴DA=DC,DE=DG,
在△DAE和△DCG中,
DA=DC∠ADE=∠CDGDE=DG,
∴△DAE≌△DCG(SAS),
∴AE=CG;
(2)成立,
理由如下:∵∠ADC=∠EDG,
∴∠ADC?∠EDC=∠EDG?∠EDC,即∠ADE=∠CDG,
在△DAE和△DCG中,
DA=DC∠ADE=∠CDGDE=DG,
∴△DAE≌△DCG(SAS),
∴AE=CG;
(3)AE⊥CG,
理由如下:延长线段AE、GC交于点H,
∵AD//BC,
∴∠CEH=∠DAE,
由(2)可知,△DAE≌△DCG,
∴∠DAE=∠DCG,
∴∠CEH=∠DCG,
∵四边形ABCD是菱形,∠ADC=90°,
∴四边形ABCD是正方形,
∴∠BCD=90°,
∴∠ECH+∠DCG=90°,
∴∠ECH+∠CEH=90°,
∴∠CHE=90°,
∴AE⊥CG.
