2020-2021鲁教版(五四制)数学七下册 -第八章 平行线的有关证明 同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021鲁教版(五四制)数学七下册 -第八章 平行线的有关证明 同步练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览

文档简介
2020-2021学年鲁教版数学七年级下册同步练习-第八章 平行线的有关证明
一、选择题
下列语句中,是命题的是(????)
A. 对顶角相等吗 B. 作∠A的平分线AD
C. 两个锐角的和大于90° D. 在线段AB上取一点C
数学中有一些命题的特征是:原命题是真命题,但它的逆命题却是假命题.例如:如果a>2,那么a2>4.下列命题中,具有以上特征的命题是(????)
A. 两直线平行,同位角相等 B. 如果|a|=1,那么a=1
C. 全等三角形的对应角相等 D. 如果x>y,那么mx>my
用三个不等式a>b,ab>0,1a<1b中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为(????)
A. 0 B. 1 C. 2 D. 3
下列命题中,是真命题的是(? ? )
A. 一个角的余角一定大于这个角 B. 互补的两个角一定有一个锐角,一个钝角
C. 如果x2>0,那么x>0 D. 1的平方是1
某班四个小组进行辩论比赛,赛前三位同学预测比赛结果如下:
甲说:“第二组得第一,第四组得第三”;
乙说:“第一组得第四,第三组得第二”;
丙说:“第三组得第三,第四组得第一”;
赛后得知,三人各猜对一半,则冠军是(????)
A. 第一组 B. 第二组 C. 第三组 D. 第四组
老师让4个学生猜一猜这次考试中4个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”,老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗?(????)
A. 甲 B. 乙 C. 丙 D. 丁
下列说法中,正确的有(????)
①关于x的方程ax=b,当a=0时,此方程无解;②若关于x的方程|x+1|+|x?1|=a有解,则a>2;③平面内有10条直线,最多可将平面分成56个部分;④钟面上从2点到4点有4次时针与分针成60°的角;⑤A、B、C、D、E、F六个足球队进行单循环比赛,当比赛到某一天时统计出A、B、C、D、E五个队分别比赛了5、4、3、2、1场球,还没有与B对比赛的球队是F队.
A. 1个 B. 2个 C. 3个 D. 4个
若“存在x>1.使x+a=1成立“是真命题,则a的取值范围是(????)
A. a<0 B. a≤0 C. a>0 D. a≥0
某工程队在修建兰宁高速公路时,有时需将弯曲的道路改直,根据什么定理可以说明这样做能缩短路程(? ? )
A. 直线的定理 B. 直线的定理或线段最短定理
C. 线段最短定理 D. 射线的定理
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 旁内角互补,两直线平行
D. 两点确定一条直线
如图,AB//CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,则下列结论正确的有(????)
①∠DFE=∠AEF;
②∠EMF=90°;
③EG//FM;
④∠AEF=∠EGC.
A. 1个
B. 2个
C. 3个
D. 4个
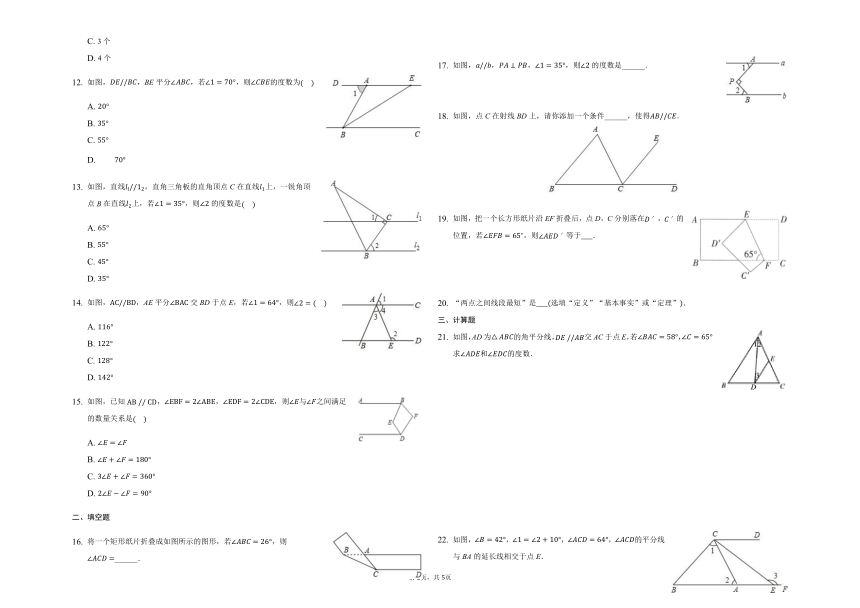
如图,DE//BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为(????)
A. 20°
B. 35°
C. 55°
D. 70°
如图,直线ll//12,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是(????)
A. 65°
B. 55°
C. 45°
D. 35°
如图,AC//BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=(????)
A. 116°
B. 122°
C. 128°
D. 142°
如图,已知AB?//?CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是(????)
A. ∠E=∠F
B. ∠E+∠F=180°
C. 3∠E+∠F=360°
D. 2∠E-∠F=90°
二、填空题
将一个矩形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=______.
如图,a//b,PA⊥PB,∠1=35°,则∠2的度数是______.
如图,点C在射线BD上,请你添加一个条件______,使得AB//CE.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65?,则∠AED′等于??????.
“两点之间线段最短”是??????(选填“定义”“基本事实”或“定理”).
三、计算题
如图,AD为△ABC的角平分线,DE?//AB交AC于点E,若∠BAC=58°,∠C=65°,求∠ADE和∠EDC的度数.
如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
如图所示:△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠CAD,∠BOA的度数是多少?
已知:三角形ABC和同一平面内的点D.
(1)如图1,点D在BC边上,DE//BA交AC于E,DF//CA交AB于F.若∠EDF=85°,则∠A的度数为______°.
(2)如图2,点D在BC的延长线上,DF//CA,∠EDF=∠A,证明:DE//BA.
(3)如图3,点D是三角形ABC外部的一个动点,过D作DE//BA交直线AC于E,DF//CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
答案
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】C
12.【答案】B
13.【答案】B
14.【答案】B
15.【答案】C
16.【答案】128°
17.【答案】55°
18.【答案】∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE
19.【答案】50?
20.【答案】基本事实
21.【答案】解:∵在△ABC中,∠BAC=58°,∠C=65°,
∴∠ABC=180°?∠BAC?∠C=57°,
∵AD是△ABC的角平分线,
∴∠BAD=12∠BAC=29°,
∵DE//AB,
∴∠ADE=∠BAD=29°,∠EDC=∠ABC=57°.
22.【答案】解:(1)结论:BF//CD.理由如下:
在三角形ABC中,∠B+∠1+∠2=180°,
∴42°+∠2+∠2+10°=180°,
∴∠2=64°,
又∵∠ACD=64°,
∴∠2=∠ACD,
∴BF//CD.
(2)∵∠ACD=64°,CE平分∠ACD,
∴∠DCE=12×64°=32°,由(1)知BF//CD,
∴∠3=180°?∠DCE=148°.
23.【答案】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°?90°?70°=20°;
∵∠BAC=60°,∠C=70°,
∴∠BAO=30°,∠ABC=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°?∠BAO?∠ABO=180°?30°?25°=125°.
故∠CAD,∠BOA的度数分别是20°,125°.
24.【答案】(1)85;
(2)?证明:如图1,延长BA交DF于G.
∵DF//CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE//BA.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
(3)
∠EDF=∠A,∠EDF+∠A=180°,
理由:如图2,∵DE//BA,DF//CA,
∴∠EDF+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠A;
如图3,∵DE//BA,DF//CA,
∴∠EDF+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
即∠EDF+∠A=180°.
一、选择题
下列语句中,是命题的是(????)
A. 对顶角相等吗 B. 作∠A的平分线AD
C. 两个锐角的和大于90° D. 在线段AB上取一点C
数学中有一些命题的特征是:原命题是真命题,但它的逆命题却是假命题.例如:如果a>2,那么a2>4.下列命题中,具有以上特征的命题是(????)
A. 两直线平行,同位角相等 B. 如果|a|=1,那么a=1
C. 全等三角形的对应角相等 D. 如果x>y,那么mx>my
用三个不等式a>b,ab>0,1a<1b中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为(????)
A. 0 B. 1 C. 2 D. 3
下列命题中,是真命题的是(? ? )
A. 一个角的余角一定大于这个角 B. 互补的两个角一定有一个锐角,一个钝角
C. 如果x2>0,那么x>0 D. 1的平方是1
某班四个小组进行辩论比赛,赛前三位同学预测比赛结果如下:
甲说:“第二组得第一,第四组得第三”;
乙说:“第一组得第四,第三组得第二”;
丙说:“第三组得第三,第四组得第一”;
赛后得知,三人各猜对一半,则冠军是(????)
A. 第一组 B. 第二组 C. 第三组 D. 第四组
老师让4个学生猜一猜这次考试中4个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”,老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗?(????)
A. 甲 B. 乙 C. 丙 D. 丁
下列说法中,正确的有(????)
①关于x的方程ax=b,当a=0时,此方程无解;②若关于x的方程|x+1|+|x?1|=a有解,则a>2;③平面内有10条直线,最多可将平面分成56个部分;④钟面上从2点到4点有4次时针与分针成60°的角;⑤A、B、C、D、E、F六个足球队进行单循环比赛,当比赛到某一天时统计出A、B、C、D、E五个队分别比赛了5、4、3、2、1场球,还没有与B对比赛的球队是F队.
A. 1个 B. 2个 C. 3个 D. 4个
若“存在x>1.使x+a=1成立“是真命题,则a的取值范围是(????)
A. a<0 B. a≤0 C. a>0 D. a≥0
某工程队在修建兰宁高速公路时,有时需将弯曲的道路改直,根据什么定理可以说明这样做能缩短路程(? ? )
A. 直线的定理 B. 直线的定理或线段最短定理
C. 线段最短定理 D. 射线的定理
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 旁内角互补,两直线平行
D. 两点确定一条直线
如图,AB//CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,则下列结论正确的有(????)
①∠DFE=∠AEF;
②∠EMF=90°;
③EG//FM;
④∠AEF=∠EGC.
A. 1个
B. 2个
C. 3个
D. 4个
如图,DE//BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为(????)
A. 20°
B. 35°
C. 55°
D. 70°
如图,直线ll//12,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是(????)
A. 65°
B. 55°
C. 45°
D. 35°
如图,AC//BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=(????)
A. 116°
B. 122°
C. 128°
D. 142°
如图,已知AB?//?CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是(????)
A. ∠E=∠F
B. ∠E+∠F=180°
C. 3∠E+∠F=360°
D. 2∠E-∠F=90°
二、填空题
将一个矩形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=______.
如图,a//b,PA⊥PB,∠1=35°,则∠2的度数是______.
如图,点C在射线BD上,请你添加一个条件______,使得AB//CE.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65?,则∠AED′等于??????.
“两点之间线段最短”是??????(选填“定义”“基本事实”或“定理”).
三、计算题
如图,AD为△ABC的角平分线,DE?//AB交AC于点E,若∠BAC=58°,∠C=65°,求∠ADE和∠EDC的度数.
如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
如图所示:△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠CAD,∠BOA的度数是多少?
已知:三角形ABC和同一平面内的点D.
(1)如图1,点D在BC边上,DE//BA交AC于E,DF//CA交AB于F.若∠EDF=85°,则∠A的度数为______°.
(2)如图2,点D在BC的延长线上,DF//CA,∠EDF=∠A,证明:DE//BA.
(3)如图3,点D是三角形ABC外部的一个动点,过D作DE//BA交直线AC于E,DF//CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
答案
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】C
12.【答案】B
13.【答案】B
14.【答案】B
15.【答案】C
16.【答案】128°
17.【答案】55°
18.【答案】∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE
19.【答案】50?
20.【答案】基本事实
21.【答案】解:∵在△ABC中,∠BAC=58°,∠C=65°,
∴∠ABC=180°?∠BAC?∠C=57°,
∵AD是△ABC的角平分线,
∴∠BAD=12∠BAC=29°,
∵DE//AB,
∴∠ADE=∠BAD=29°,∠EDC=∠ABC=57°.
22.【答案】解:(1)结论:BF//CD.理由如下:
在三角形ABC中,∠B+∠1+∠2=180°,
∴42°+∠2+∠2+10°=180°,
∴∠2=64°,
又∵∠ACD=64°,
∴∠2=∠ACD,
∴BF//CD.
(2)∵∠ACD=64°,CE平分∠ACD,
∴∠DCE=12×64°=32°,由(1)知BF//CD,
∴∠3=180°?∠DCE=148°.
23.【答案】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°?90°?70°=20°;
∵∠BAC=60°,∠C=70°,
∴∠BAO=30°,∠ABC=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°?∠BAO?∠ABO=180°?30°?25°=125°.
故∠CAD,∠BOA的度数分别是20°,125°.
24.【答案】(1)85;
(2)?证明:如图1,延长BA交DF于G.
∵DF//CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE//BA.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
(3)
∠EDF=∠A,∠EDF+∠A=180°,
理由:如图2,∵DE//BA,DF//CA,
∴∠EDF+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠A;
如图3,∵DE//BA,DF//CA,
∴∠EDF+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
即∠EDF+∠A=180°.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
